Sınıf 8 ➤ ÖRNEK SORULAR ➤ OCAK 2020
LİSELERE GİRİŞ SINAVI-ÖRNEK SORULAR
OCAK 2020-LGS MATEMATİK-ÖRNEK SORULARININ ÇÖZÜMLERİ
Bu sayfada, MEB’in yayınladığı 2019-2020 LGS Ocak ayı örnek sorularının çözümlerini bulabilirsiniz. Soruları görmek için bu bağlantıyı tıklayabilirsiniz.
DİĞER AYLARIN ÖRNEK SORULARI VE ÇÖZÜMLERİ İÇİN TIKLAYIN!
ÖRNEK SORU 1’in Çözümü
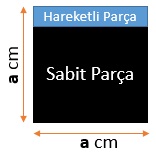
Şekil 1’de verilen uzunluklara göre, tüm klaketin alanı a . a = a2 cm2’dir.
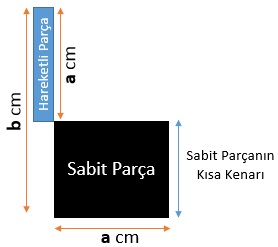
Dikdörtgen şeklindeki sabit parçanın uzun kenarı a cm ve kısa kenarı b – a cm uzunluğundadır. Buna göre, sabit parçanın alanı a . (b – a) = ab – a2 cm2’dir.
Hareketli parçanın alanını bulabilmek için tüm alandan sabit parçanın alanını çıkarabiliriz.
(Hareketli parçanın alanı) = (Tüm alan) – (Sabit parçanın alanı)
= a2 – (ab – a2)
= 2a2 – ab cm2
CEVAP: D
ÖRNEK SORU 2’nin Çözümü
Tangram parçaları ile oluşturulan figürün boyu, tangramın köşegen uzunluğuna eşittir(*). Her ikisi de mavi ve pembe üçgenlerin dik kenarları ile gri karenin bir kenarının toplam uzunluğu kadardır. Buna göre, kare şeklindeki tangramın bir kenarı x cm olmalıdır.
Çerçeve kalınlığı 1 cm olduğu için tangram ve çerçevenin beraber oluşturduğu karenin bir kenarı x + 2 cm’dir.
Kenar uzunluklarını kullanarak karelerin alanlarını aşağıdaki gibi bulabiliriz.
- Tangramın alanı: x . x = x2 cm2
- Çerçeveyle beraber tangramın alanı: (x + 2)(x + 2) = x2 + 4x + 4 cm2
Santimetre cinsinden çerçevenin alanını bulabilmek için x2 + 4x + 4’ten x2’yi çıkarmamız gerekir.
Çerçevenin alanı = x2 + 4x + 4 - x2 = 4x + 4
NOT: Bu eşitliğin net bir şekilde görülebilmesi için tangramın ve oluşturulan şeklin kareli veya noktalı kâğıt üzerinde verilmesi gerektiğini düşünüyoruz.
CEVAP: C
ÖRNEK SORU 3’ün Çözümü
2,043’ün doğru çözümlemesi
2,043 = 2 . 100 + 4 . 10–2 + 3 . 10–3 ve
2,702’nin doğru çözümlemesi
2,702 = 2 . 100 + 7 . 10–1 + 2 . 10–3’tür.
8 öğrenci bitter ve 7 öğrenci beyaz çikolatalı gofretin yağ miktarlarını doğru çözümlemiştir. Buna göre, Bülent öğretmen 8 bitter ve 7 beyaz çikolatalı gofret dağıtmıştır. Elinde 13 bitter çikolatalı gofret olduğuna göre, sınıfa 13 + 8 = 21 bitter ve 21 beyaz çikolatalı gofret getirmiştir. 7’sini dağıttığı için geriye 21 – 7 = 14 beyaz çikolatalı gofret kalmıştır.
CEVAP: B
ÖRNEK SORU 4’ün Çözümü
Mehmet Amca dekar başına 180 kg fındık ve 100 kg kivi üretmektedir. Her biri 10’ar dekar olan iki bahçesi olduğu için bu bahçelerdeki toplam üretimi 180 . 10 = 1800 kg fındık ve 100 . 10 = 1000 kg kividir.
Satılan balın en fazla kaç kg olduğunu bulabilmek için fındık ve kivinin en düşük satış fiyatlarını temel almamız gerekir. Soruda açıkça belirtilmediği halde, fiyat aralıklarına sınır noktaları dâhil değildir. Fındığın en düşük kg satış fiyatı 12 ₺ ve kivinin en düşük kg satış fiyatı 4 ₺’dir. Bu değerler üzerinden hesaplandığında fındık ve kividen elde edilen toplam gelir
12 . 1800 + 4 . 1000 = 25 600 ₺
olur. Buna göre, bal satışından en fazla
53 500 – 25 600 = 27 900 ₺
gelir elde edilmiştir. 27 900 ₺’yi balın en düşük fiyatı olan 31 ₺’ye bölerek en fazla kaç kg bal satıldığını bulabiliriz.
27 900 ÷ 31 = 900 kg
CEVAP: B
ÖRNEK SORU 5’in Çözümü
Zemin katın 0. kat ve 0’ın tam kare olduğu varsayıldığında tüm asansörler zemin katta durur(*). Bu durumda Ersin Bey şekildeki 4 asansörden herhangi birine binmiş olabilir. İstenilen olasılığı bulabilmek için verilen 4 asansörden kaçının 16. katta durduğunu bulmamız gerekir.
- 1. asansör: Tüm katlarda durduğu için 16. katta da durur.
- 2. asansör: 16 asal olmadığı için 16. katta durmaz.
- 3. asansör: 16 tam kare olduğu için 16. katta durur.
- 4. asansör: 16 = 24 olduğu için 16. katta durur.
4 asansörden 3’ü 16. katta durduğuna göre Ersin Bey’in bindiği asansörün istediği katta durma olasılığı ...’tür.
NOT: 0’ın tam kare sayılmadığı durumda 3. asansör zemin katta durmayacağı için Ersin Bey bu asansöre binmiş olamaz. Geriye kalan 3 asansörden 2’si 16. kata çıktığı için istenilen olasılık ... olur. Soruyu netleştirmek adına, Ersin Bey asansöre binerken tüm asansörlerin zemin katta bulunduğu belirtilebilirdi.
CEVAP: D
ÖRNEK SORU 6’nın Çözümü
Görseldeki kalemtıraş cetveldeki ölçeğe göre 2 cm’den kısa olduğu ve kapağın kutuyu ne kadar kapattığı, kapağın kalemtıraşın sağında kalan bölgeye girip girmediği vb. bilgiler belirtilmediği için maalesef bu sorunun da net olmadığını düşünüyoruz. Yine de kalemtıraş boyunun cetvelin açıkta kalan kısmın uzunluğuna eşit olduğunu varsayarsak, bu uzunluğun 2 cm ve 3 cm arasında ve 3’e daha yakın olduğu sonucuna varabiliriz.
Seçeneklerdeki sayıları tamamen karekök içerisine alıp, hangisinin 2 ile 3 arasında ve 3’e daha yakın olduğunu bulalım.
A) ... ...
18 sayısı 42 = 16 ile 52 = 25 arasında ve 16’ya daha yakındır. Dolayısıyla, ..., 4 ile 5 arasında ve 4’e daha yakındır.
B) ... ...
12 sayısı 32 = 9 ve 42 = 16 arasında ve 9’a daha yakın olduğu için ..., 3 ile 4 arasında ve 3’e daha yakındır.
C) ... ...
8 sayısı 22 = 4 ile 32 = 9 arasında ve 9’a daha yakındır. Bu nedenle ..., 2 ile 3 arasında ve 3’e daha yakındır.
D) 6 sayısı 22 = 4 ile 32 = 9 arasında ve 4’e daha yakındır. Bu nedenle ... sayısı 2 ile 3 arasında ve 2’ye daha yakındır.
CEVAP: C
ÖRNEK SORU 7’nin Çözümü
Her marka baldan elde edilen gelir, en az satış fiyatlarının EKOK’u kadar olabilir.
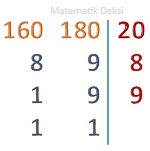
EKOK (160, 180) = 20 . 8 . 9 = 1440
olduğundan A ve B marka balların her birinden en az 1440 ₺ gelir elde edilmiştir. Buna göre,
- A marka baldan en az 1440 ÷ 160 = 9 kavanoz ve
- B marka baldan en az 1440 ÷ 180 = 8 kavanoz
satılmıştır. Satılan toplam kütleyi bulabilmek için kavanoz sayıları ile kütleleri çarpmamız gerekir.
Toplam ağırlık = 9 . 600 + 8 . 800
= 5400 + 6400
= 11 800 gr
= 11,8 kg
CEVAP: C
ÖRNEK SORU 8’in Çözümü
2 kepenk genişliğinin 1 m fazlası ... m olduğu için 2 kepengin toplam genişliği ... m ve 1 kepengin genişliği ... ... ... m’dir.
Soldaki kepengin kapalı kısmının yüksekliği ... m olduğundan kapladığı alan ... ... m2’dir.
Sağdaki kepengin kapalı kısmının yüksekliği ise 1 m’dir. Buna göre, kapladığı alan ... ... m2’dir.
Yukarıda elde ettiğimiz bilgilere göre kapalı bölgeler arasındaki fark
... ...
... ...
... m2’dir.
CEVAP: D
ÖRNEK SORU 9’un Çözümü
Bir bütünün % 12,5’i, ...’ine eşittir. Buna göre,
- % 12,5 küçültülen bir şekil ... ...’ine düşer.
- % 12,5 büyültülen bir şekil ... ...’ine çıkar.
Büyültme-küçültme işlemleri yaptıktan sonra elde edilen şekillerin alanları arasındaki fark, orijinal şeklin ... ...’ü kadardır. Ayrıca, orijinal şekillerde 4’er kare olduğundan her bir karenin alanı da bu şekillerin ...’ü kadardır. Buna göre, bir karenin alanı 4x2 + 12x + 9 cm2’ye eşittir.
4x2 + 12x + 9 = (2x + 3)2
olduğundan, karenin bir kenar uzunluğu 2x + 3 cm’dir.
CEVAP: B
ÖRNEK SORU 10’un Çözümü
Doğru yanıtta,
- sarı kartın solundaki ifade x2 – 8x + 16’ya
- mavi kartın sağındaki ifade x2 – 16’ya ve
- sarı kartın sağındaki ifade mavi kartın solundaki ifadeye
özdeş olmalıdır. Bu şartları sağlayan tek seçenek A’dır.
- x2 – 8x + 16 = (x – 4)(x – 4)
- (x – 4)(x + 4) = x2 – 16
- x(x – 9) = x2 – 9x
CEVAP: A
Sınıf 8 ➤ ÖRNEK SORULAR ➤ OCAK 2020
