Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2015-2016 1.DÖNEM MAZERET-SORU VE ÇÖZÜMLERİ
LİSELERE GİRİŞ SINAVI
2015-2016 TEOG 1. DÖNEM MAZERET SINAVI - Çıkmış Sorular ve Çözümleri
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
400 000 × 9000 işleminin sonucunun bilimsel gösterimi aşağıdakilerden hangisidir?
Çözüm:
400 000 = 4 . 105 ve 9000 = 9 . 103 olduğu için bu sayıların çarpımı
4 . 105 × 9 . 103 = 36 . 105 + 3 = 36 . 108'e
eşittir. Bu sonucun bilimsel gösterimi 3,6 . 109'dur.
CEVAP: A
Aşağıdaki sayılardan hangisi 2–6 sayısına eşit değildir?
Çözüm:
A, B ve C seçeneklerindeki ifadeler 2–6'ya eşittir. D seçeneğindeki ifade ise 2–6 şeklinde yazılamaz.
CEVAP: D
Bir ayrıtının uzunluğu a metre olan küpün hacmi a3'tür.
Buna göre ayrıtlarından birinin uzunluğu 0,4 metre olan küp şeklindeki bir akvaryum en fazla kaç metreküp su alır?
Çözüm:
0,4 sayısı ...'a eşittir. Bu sayının küpü ise
... ... ...'dir
Bulduğumuz sonucun ondalık gösterimi 0,064'tür.
CEVAP: C

Şekilde kenar uzunlukları verilen ABCD karesinin alanının, EFGH dikdörtgeninin alanına oranı kaçtır?
Çözüm:
ABCD karesinin alanı 63 . 63 = 63 + 3 = 66 cm2'dir.
EFGH dikdörtgeninin alanı ise 32 . 22 = (3 . 2)2 = 62 cm2'dir.
Bu alanların oranı
...'e
eşittir.
CEVAP: D
Alanı ... cm2 olan dikdörtgenin kenarlarından birinin uzunluğu 4 cm olduğuna göre diğer kenarının uzunluğu kaç santimetredir?
Çözüm:
Alanı, verilen kenar uzunluğuna bölerek, istenilen kenar uzunluğunu bulabiliriz.
... ... ... ... cm
CEVAP: A
... ... işleminin sonucu kaçtır?
Çözüm:
- ... ...
- ...
- ... ...
Yukarıda bulduğumuz ifadeleri işlemde yerlerine yazarak sonucu elde edebiliriz.
... ... ... ...
CEVAP: D
95 . 3–2 işleminin sonucu aşağıdakilerden hangisidir?
Çözüm:
9 = 32 olduğu için 95 = (32)5 = 32 . 5 = 310'dur.
310 ile 3–2'nin çarpımı ise 310 . 3–2 = 310 – 2 = 38'e eşittir.
CEVAP: B
210 sayfalık bir kitabın her gün 16 sayfasını okuyan Çağla, bu kitabın tamamını kaç günde okur?
Çözüm:
Çağla'nın bu kitabı kaç günde okuduğunu bulabilmek için 210'u 16'ya böleriz. Bölme işleminde 16 yerine bu sayıya eşit olan 24'ü yazarsak, sonucun 26'ya eşit olduğunu görebiliriz.
...
CEVAP: B
... ... eşitliğinde ... yerine hangisi yazılmalıdır?
Çözüm:
... ... ... ...
olduğundan ...'dir.
CEVAP: A
Aşağıdaki çarpma işlemlerinin hangisinin sonucu bir tam kare sayı değildir?
Çözüm:
Bu soruyu birkaç farklı yolla çözebiliriz. Örneğin, seçenekleri asal çarpanlarına ayırıp, bulduğumuz ifadelerin tam kare olup olmadığına bakabiliriz. Asal çarpanlarına ayrılmış bir sayının tam kare olabilmesi için tüm asal çarpanların kuvvetlerinin çift olması gerektiğini hatırlayalım.
CEVAP: D
Alanı 1,69 cm2 olan bir karenin bir kenarının uzunluğu kaç santimetredir?
Çözüm:
Karenin kenar uzunluğunu bulabilmek için alanının karekökünü alırız.
... ... ... ... ... cm
CEVAP: C
... ve ... birer doğal sayıdır.
... sayısı ... biçiminde yazıldığında ...’nın en büyük değeri için ... kaç olur?
Çözüm:
...'yi farklı ... biçimlerinde yazabiliriz. Yalnız, ...'nın en büyük değerini bulabilmek için tam kare çarpanların tümünü kök dışına çıkarmamız gerekir.
...
Buna göre ...'dir.
CEVAP: B
Bir aritmetik dizinin terimleri olan 30 ve 54 sayıları arasında bu dizinin üç terimi daha bulunmaktadır.
Aşağıdakilerden hangisi bu üç terimden biridir?
Çözüm:
Bu aritmetik dizide iki komşu terim arasındaki fark x ise, 30 ile 54 arasındaki farkın 4x'e eşit olması gerekir. 54 – 30 = 24 sayısı 4x'e eşitse, x = 6'dır. 30'dan başlayıp, 6 ekleye ekleye devam ettiğimizde, soruda verilen dizinin elemanlarının
30, 36, 42, 48, 54
olduğunu görebiliriz. C seçeneğindeki 42 sayısı 30 ile 54 arasındaki terimlerden biridir.
CEVAP: C
... sayısı aşağıdaki sayı kümelerinden hangisinin elemanı değildir?
Çözüm:
Kök içerisinde bir tam kare sayı olduğu için ... hem tam sayı hem doğal sayı hem de rasyonel sayıdır. Rasyonel sayıların hiçbiri irrasyonel sayılar kümesinin elemanı değildir.
CEVAP: B
Kenar uzunlukları ... cm ve ... cm olan bir dikdörtgenin çevresi kaç santimetredir?
Çözüm:
Kenar uzunluklarında gösteren ifadelerde mümkün olan tüm çarpanları kök dışına çıkaralım.
- ...
- ...
Yukarıda bulduğumuz ifadeleri çevre formülünde yerlerine yazarak aşağıdaki sonucu elde edebiliriz.
... ... ... ... cm
CEVAP: D

Dikdörtgen şeklindeki kartondan, alanları 81 cm2, 36 cm2 ve 25 cm2 olan kare şeklindeki üç parça şekildeki gibi kesilerek çıkarılıyor.
Buna göre kalan karton parçasının çevresi kaç santimetredir?
Çözüm:
Geriye kalan karton parçasının çevresini hesaplayabilmek için öncelikle kesilen karelerin kenar uzunluklarını bulmamız gerekir.
- En büyük karenin bir kenar uzunluğu: ... cm
- Ortanca karenin bir kenar uzunluğu: ... cm
- En küçük karenin bir kenar uzunluğu: ... cm
Karelerin kenar uzunluklarını kullanarak verilen şeklin kenar uzunluklarını hesaplayabiliriz.

Kenar uzunluklarını topladığımızda, şeklin çevresinin
CEVAP: A
Aşağıdaki çarpma işlemlerinden hangisinin sonucu bir tam sayı değildir?
Çözüm:
A) ...
...
...
... ↣
B) ...
...
...
...
... ↣
C) ...
...
... ↣
D) ...
...
...
... ↣
Sadece B seçeneğindeki işlemin sonucu tam sayı değildir.
CEVAP: B
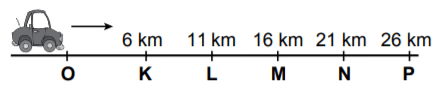
Şekilde O noktasında bulunan bir aracın K, L, M, N, P noktalarına uzaklıkları verilmiştir.
Bu araç ok yönünde ... km yol aldığında bulunduğu yer, hangi ardışık iki nokta arasında olur?
Çözüm:
210'dan büyük ve 210'a en yakın tam kare sayı 152 = 225'tir. Bu nedenle, ... sayısı 14 ile 15 arasındadır. 14 ile 15 arasındaki bir nokta, aynı zamanda L ile M noktaları arasındadır.
CEVAP: D
a ve b birer doğal sayı olmak üzere aşağıdakilerden hangisi ... şeklinde yazılamaz?
Çözüm:
CEVAP: A
Aşağıdakilerden hangisindeki eşitlik, x yerine yazılan her gerçek sayı için doğru olur?
Çözüm:
Soruda hangi eşitliğin bir özdeşlik olduğu sorulmaktadır.
A) Sağdaki parantezi açarsak, 2x – 14 ifadesini elde ederiz. Yalnız bu ifade, eşitliğin sol tarafındaki ifade ile aynı değildir. Bu nedenle A
seçeneğindeki eşitlik bir
B) Soldaki parantezi açarsak, x2 – x ifadesine ulaşırız. Bu ifade eşitliğin sağındaki ifadeden farklıdır. Bu nedenle B seçeneğindeki eşitlik
bir
C) Sol taraftaki parantezi açtığımızda, 4 – 2x2 ifadesini elde ederiz. Sabit terimle x'li terimin yerini değiştirdiğimizde, ifade
–2x2 + 4 haline dönüşür. Bu seçenekte verilen eşitlik bir
D) Sağdaki parantezi açarsak, 10 – 5x ifadesini elde ederiz ve bu ifade eşitliğin sol tarafındaki ifade ile aynı değildir. D seçeneğindeki eşitlik de
bir
CEVAP: C
Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2015-2016 1.DÖNEM MAZERET-SORU VE ÇÖZÜMLERİ