2016-2017 TEOG 1. DÖNEM - Çıkmış Sorular ve Çözümleri

Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2016-2017 1.DÖNEM SORU VE ÇÖZÜMLERİ

LİSELERE GİRİŞ SINAVI

2016-2017 TEOG 1. DÖNEM - Çıkmış Sorular ve Çözümleri

Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.

Soru 1:

12 . 12 . 12 . 12 çarpımı aşağıdakilerden hangisine eşittir?

A) 4 . 12

B) 12⁴

C) 4¹²

D) 12¹²

Çözüm:

4 tane 12'nin çarpımı 12'nin 4. kuvvetine eşittir. 12'nin 4. kuvvetinin doğru gösterimi B seçeneğinde verilmiştir.

CEVAP: B

Soru 2:

Aşağıdaki ondalık gösterimlerden hangisinin çözümlenmiş biçiminde 5 × 10^–3 ifadesi bulunur?

A) 32,305

B) 47,502

C) 568,04

D) 5017,2

Çözüm:

Yöntem 1:

5 × 10^–3'ün ondalık gösterimi 0,005'tir. Buna göre, aradığımız seçenekteki sayının binde birler basamağında 5 olmalıdır. Binde birler basamağında 5 olan tek seçenek ise A'dır.

Yöntem 2:

Verilen seçeneklerin çözümlemesini yaptığımızda da, verilen ifadenin sadece A seçeneğinde bulunduğunu görebiliriz.

A) 32,305 = 3 × 10¹ + 2 × 10⁰ + 3 × 10^–1 + 5 × 10^–3

B) 47,502 = 4 × 10¹ + 7 × 10⁰ + 5 × 10^–1 + 2 × 10^–3

C) 568,04 = 5 × 10² + 6 × 10¹ + 8 × 10⁰ + 4 × 10^–2

C) 5017,2 = 5 × 10³ + 1 × 10¹ + 7 × 10⁰ + 2 × 10^–1

CEVAP: A

Soru 3:

Aşağıdaki sayılardan hangisinin asal çarpanları 2, 3 ve 5'tir?

A) 110

B) 100

C) 90

D) 72

Çözüm:

Çarpan ağacı yöntemini kullanarak verilen sayıların asal çarpanlarını bulabiliriz.

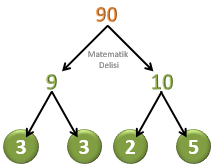
Yukarıda oluşturduğumuz çarpan ağaçlarına göre

110'un asal çarpanları 2, 5 ve 11;
100'ün asal çarpanları 2 ve 5;
90'ın asal çarpanları 2, 3 ve 5;
72'nin asal çarpanları 2 ve 3'tür.

CEVAP: C

Soru 4:

Altuğ'un aklından tuttuğu sayının asal çarpanlarının en küçüğü 5, en büyüğü 11'dir.

Buna göre Altuğ'un aklından tuttuğu sayı aşağıdakilerden hangisi olabilir?

A) 110

B) 165

C) 180

D) 275

Çözüm:

Çarpan ağacı yöntemini kullanarak verilen sayıların asal çarpanlarını bulabiliriz.

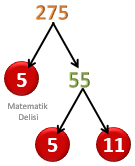
Yukarıda oluşturduğumuz çarpan ağaçlarına göre,

110'un asal çarpanları 2, 5 ve 11;
165'in asal çarpanları 3, 5 ve 11;
180'in asal çarpanları 2, 3 ve 5;
275'in asal çarpanları 5 ve 11'dir.

CEVAP: D

Soru 5:

Bir merdivenin basamakları üçer üçer veya dörder dörder inildiğinde her seferinde 1 basamak artıyor.

Buna göre bu merdiven en az kaç basamaklıdır?

A) 11

B) 13

C) 23

D) 25

Çözüm:

Basamak sayısı, şu ankinden 1 tane az olsaydı, hem 3'ün hem de 4'ün tam katı olurdu. 3 ve 4'ün ortak katlarından en küçüğü 12'dir.

EKOK(3, 4) = 12

Buna göre, merdivendeki basamak sayısı en az 12 + 1 = 13'tür.

CEVAP: B

Soru 6:

A = 2⁴ . 3³ . 5²

B = 2³ . 3² . 5² . 7

Yukarıda üslü biçimde ifade edilen A ve B sayılarının en küçük ortak katının, en büyük ortak bölenine oranı kaçtır?

A) 7

B) 21

C) 42

D) 210

Çözüm:

EBOB:

Asal çarpanlarına ayrılmış iki sayının EBOB'unu hesaplayabilmek için bu sayılarda hangi asal çarpanların ortak olduğunu buluruz. Her bir ortak asal çarpan için sayılardaki kuvvetleri karşılaştırır, küçük olan kuvveti asal çarpanın üzerine yazarız. Bu şekilde oluşturduğumuz üslü ifadelerin çarpımı EBOB'u verir.

2 ortak asal çarpandır. Kuvveti küçük olan ifade 2³'tür.
3 ortak asal çarpandır. Kuvveti küçük olan ifade 3²'dir.
5 ortak asal çarpandır. Kuvveti küçük olan ifade 5²'dir.
7 ortak asal çarpan değildir.

Elde ettiğimiz üslü ifadelerin çarpımı EBOB'u verir.

EBOB(A, B) = 2³ . 3² . 5²

EKOK:

EKOK'u veren ifadede yalnız ortak asal çarpanlar değil, aynı zamanda ortak olmayan asal çarpanlar da bulunur. Ortak olmayan bir asal çarpanın kuvveti bulunduğu sayıdakine, ortak bir asal çarpanın kuvveti ise sayılardaki kuvvetlerden büyük olana eşittir.

2 ortak asal çarpandır. Kuvveti büyük olan ifade 2⁴'tür.
3 ortak asal çarpandır. Kuvveti büyük olan ifade 3³'tür.
5 ortak asal çarpandır. Kuvveti büyük olan ifade 5²'dir.
7 ortak asal çarpan değildir. B sayısındaki kuvveti 1'dir.

Elde ettiğimiz üslü ifadelerin çarpımı EKOK'u verir.

EKOK(A, B) = 2⁴ . 3³ . 5² . 7

EBOB-EKOK Oranı:

EKOK'u EBOB'a bölüp, sadeleştirmeleri yapalım.

... ... ... ...

CEVAP: C

Soru 7:

Bir toplantıya 5³ ülkenin her birinden eşit sayıda kişi katılmıştır. Bu kişiler, bir otelin 5⁴ odasının her birinde 5 kişi kalacak şekilde odalara yerleştirilmiştir.

Buna göre bu toplantıya bir ülkeden kaç kişi katılmıştır?

A) 5⁸

B) 5⁶

C) 5⁴

D) 5²

Çözüm:

Toplantıya katılan kişi sayısı, 5⁴ odada kalan kişi sayısına eşittir. Bir odada 5 kişi kaldığına göre, toplantıya katılan toplam kişi sayısı 5⁴ . 5 = 5^{4 + 1} = 5⁵'tir.

5⁵ kişi 5³ faklı ülkeden geldiğine ve her ülkeden gelen kişi sayısı aynı olduğuna göre, bir ülkeden gelen kişi sayısı ...'dir.

CEVAP: D

Soru 8:

Aralarında asal iki doğal sayının toplamı 15'tir.

Buna göre bu sayıların çarpımı aşağıdakilerden hangisi olamaz?

A) 26

B) 44

C) 54

D) 56

Çözüm:

İki doğal sayının toplamı 15 ise bu sayılar

0 ve 15;
1 ve 14;
2 ve 13;
3 ve 12;
4 ve 11;
5 ve 10;
6 ve 9; veya
7 ve 8

olabilir. Bu sayıların çarpımlarına baktığımızda

A seçeneğindeki sayının 2 × 13'e,
B seçeneğindeki sayının 4 × 11'e,
C seçeneğindeki sayının 6 × 9'a ve
D seçeneğindeki sayının 7 × 8'e

eşit olduğunu görebiliriz. C seçeneğini veren 6 ve 9 sayılarının ikisi de 3'e kalansız bölündüğü için bu sayılar aralarında asal değildir. Soruda bahsedilen sayıların çarpımı 54 olamaz.

CEVAP: C

Soru 9:

a = 2⁴ ve b = 5⁴ olduğuna göre a . b işleminin sonucu aşağıdakilerden hangisine eşittir?

A) 7⁴

B) 10⁴

C) 10⁸

D) 10¹⁶

Çözüm:

a ve b için verilen üslü ifadelerin kuvvetleri aynı olduğu için tabanlarını çarparız.

a . b = 2⁴ . 5⁴ = (2 . 5)⁴ = 10⁴

CEVAP: B

Soru 10:

Aşağıdaki eşitliklerden hangisi doğrudur?

A) 1672 × 10¹⁸ = 1,672 × 10¹⁵

B) 16,72 × 10¹⁸ = 167,2 × 10¹⁷

C) 1,672 × 10¹⁵ = 16,72 × 10¹⁶

D) 0,1672 × 10¹⁴ = 167,2 × 10¹⁷

Çözüm:

Virgülü bir basamak sağa kaydırdığımızda 10'un kuvveti 1 azalır; bir basamak sola kaydırdığımızda ise 10'un kuvveti 1 artar.

Bu kurala uyan tek seçenek B'dir.

16,72 × 10¹⁸ = 16,72 × 10 . 10¹⁷ = 167,2 × 10¹⁷

CEVAP: B

Soru 11:

Bir basamaklı en büyük tam kare sayı ile üç basamaklı en küçük tam kare sayının toplamı kaçtır?

A) 130

B) 125

C) 116

D) 109

Çözüm:

Bir basamaklı en büyük tam kare sayı 9'dur.
Üç basamaklı en küçük tam kare sayı 100'dür.

Bu iki sayının toplamı 9 + 100 = 109 yapar.

CEVAP: D

Soru 12:

Üslü sayılarla işlemler- 2016-2017 teog 1. dönem sorusu

Şekildeki eşit kollu terazi dengededir. Terazinin bir kefesinde 8³ gramlık bir kütle, diğerinde 2^x gramlık bir kütle bulunmaktadır.

Buna göre x kaçtır?

A) 3

B) 6

C) 9

D) 12

Çözüm:

Terazi dengede olduğuna göre sol ve sağ kefedeki ağırlıkların aynı olması gerekir.

8³ = 2^x

8 yerine 2³ yazarsak, eşitliğin solundaki sayının 8³ = (2³)³ = 2^{3 . 3} = 2⁹'a eşit olduğunu görürüz. Eşitliğin solunda ve sağında aynı tabana sahip üslü ifadeler elde ettiğimiz için kuvvetlerin de eşit olması gerekir.

x = 9

CEVAP: C

Soru 13:

... sayısı aşağıdakilerden hangisi ile çarpılırsa sonuç bir doğal sayı olur?

A) ...

B) ...

C) ...

D) ...

Çözüm:

... ... ve
... ...'dir.

Bu iki sayının çarpımı bir tam sayıya eşittir.

... ...

CEVAP: D

Soru 14:

Alanı 64 cm² ile 144 cm² arasında olan bir karenin çevresi santimetre cinsinden aşağıdakilerden hangisi olabilir?

A) 28

B) 43

C) 51

D) 56

Çözüm:

Karenin alanı 64 cm² olsaydı, bir kenarı ... cm ve çevresi 4 × 8 = 32 cm olurdu.
Karenin alanı 144 cm² olsaydı, bir kenarı ... cm ve çevresi 4 × 12 = 48 cm olurdu.

Bu karenin alanı 64 cm² ile 144 cm² arasında ise çevresi 32 cm ile 48 cm arasında olmalıdır. Seçeneklerdeki sayılardan 32 ile 48 arasında olan tek sayı 43'tür.

CEVAP: B

Soru 15:

... ve ... olduğuna göre ... kaçtır?

A) 13

B) 19

C) 103

D) 109

Çözüm:

99 = 3² . 11 olduğu için ... ...'dir. Buna göre m = 3'tür.
1000 = 10² . 10 olduğu için ... ...'dur. Buna göre n = 10'dur.

Yukarıda elde ettiğimiz sonuçlara göre m + n = 3 + 10 = 13'tür.

CEVAP: A

Soru 16:

2016-2017 TEOG 1. dönem kareköklü sayı sorusu

Şekildeki sayı doğrusunda L noktasına karşılık gelen sayı 9'dur.

K ile L noktaları arasındaki uzaklık ... birim olduğuna göre K noktasına karşılık gelen sayı aşağıdaki hangi iki sayı arasındadır?

A) 2 ile 3

B) 3 ile 4

C) 4 ile 5

D) 5 ile 6

Çözüm:

Sayı doğrusunda 9'un ... birim solundaki nokta ...'dir.

27'den küçük ve 27'ye en yakın tam kare sayı 5²'dir. Bu nedenle ... sayısı 5 ile 6 arasındadır.

... ifadesinde ... yerine sırasıyla 6 ve 5 sayılarını koyarak, bu ifadenin 3 ile 4 arasında olduğunu görebiliriz.

CEVAP: B

Soru 17:

... devirli ondalık gösterimine eşit olan rasyonel sayı aşağıdakilerden hangisidir?

A) ...

B) ...

C) ...

D) ...

Çözüm:

... ... ... ...

CEVAP: C

Soru 18:

0,000000002 sayısının bilimsel gösterimi a × 10ⁿ'dir.

Buna göre a × n kaçtır?

A) –18

B) –16

C) 16

D) 18

Çözüm:

Bilimsel gösterimde virgülün solunda sıfırdan farklı bir rakam olması gerekir. Bu nedenle a = 2'dir. Virgülü 1 basamak sağa kaydırdığımızda 10'un kuvvetini 1 azaltırız. Bu kuralı kullandığımızda n'nin –9'a eşit olduğunu görebiliriz.

a × n = 2 × (–9) = –18

CEVAP: A

Soru 19:

Kenarlarının uzunlukları ... metre ve ... metre olan dikdörtgen şeklindeki bir bahçenin 1 metrekaresi sulanırken bir yılda ... metreküp su kullanılmaktadır.

Buna göre bu bahçenin tamamını sulamak için bir yılda kaç metreküp su gerekir?

A) ...

B) ...

C) ...

D) ...

Çözüm:

Bu bahçenin alanı ... metrekaredir.

1 metrekare için ... metreküp su kullanıldığına göre, ... metrekare için ... ... metreküp su kullanılır.

CEVAP: B

Soru 20:

... işleminin sonucu kaçtır?

A) ...

B) ...

C) ...

D) ...

Çözüm:

... ... ... ... ... ...

CEVAP: A

Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2016-2017 1.DÖNEM SORU VE ÇÖZÜMLERİ