2014-2015 TEOG 2. DÖNEM SORU VE ÇÖZÜMLERİ

Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2014-2015 2.DÖNEM SORU VE ÇÖZÜMLERİ

LİSELERE GİRİŞ SINAVI

2014-2015 TEOG 2. DÖNEM - Çıkmış Sorular ve Çözümleri

Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.

Soru 1:

Yukarıda verilen sayılardan hangileri rasyonel sayıdır?

A) I ve II

B) II ve III

C) II ve IV

D) III ve IV

Çözüm:

Bu soruyu çözebilmek için Kareköklü Sayılarda Çarpma ve Bölme ve Ondalık Gösterimin Karekökü konularında öğrendiğimiz bilgileri kullanıyoruz.

III: Karekök içerisindeki sayıyı kök dışına çıkardığımızda, payı ve paydası tam sayı olan bir kesirle karşılaşırız.

... ... ... ...

IV: Bu sayıyı da payı ve paydası tam sayı olan bir kesir şeklinde yazabiliriz.

... ... ... ... ...

III ve IV'te verilen sayılar rasyoneldir.

CEVAP: D

Soru 2:

2014-2015 Üçgenlerde Eşlik-Benzerlik Sınav Sorusu

Şekildeki F, G, H ve T noktalarından hangisi [DE]'nın uç noktalarıyla birleştirilirse ABC üçgenine eş bir üçgen elde edilir?

A) F

B) G

C) H

D) T

Çözüm:

Bir üçgenin ABC üçgenine eş olabilmesi için tüm kenar uzunluklarının ABC'ninkilerle aynı olması gerekir. [DE] doğru parçası, bu üçgenin kenarlarından biridir ve uzunluğu |AB|'ye eşittir. Buna göre, ABC'ye eş olan üçgenin diğer iki kenar uzunluğu |BC| ve |AC| ile aynı olmalıdır.

|BC| uzunluğu, dik kenarları 1 ve 3 birim olan bir dik üçgenin hipotenüsüne eşittir. Bu mesafe, F ve D noktaları arasındaki uzaklığa eşit olduğu için F noktasının [DE]'nin uç noktaları ile birleştirilmesiyle elde edilen üçgen, ABC'ye eştir.

2014-2015 Üçgenlerde Eşlik-Benzerlik Sınav Sorusunun Çözümü

CEVAP: A

Soru 3:

7⁸ : 7^a = 7^–4 olduğuna göre, a kaçtır?

A) –12

B) –2

C) 2

D) 12

Çözüm:

...

olduğu için 8 – a ifadesi –4'e eşittir.

8 – a = –4

⇒ 8 + 4 = a

⇒ a = 12

CEVAP: D

Soru 4:

Alanı 288 cm² olan karenin çevre uzunluğu ile bir eşkenar üçgenin çevre uzunluğu birbirine eşittir.

Buna göre, eşkenar üçgenin bir kenar uzunluğu kaç santimetredir?

A) ...

B) ...

C) ...

D) ...

Çözüm:

288 = 2⁵ . 3²'dir. Buna göre karenin kenar uzunluğu ... ... ... cm'dir.

Karenin çevresi, bir kenar uzunluğunun 4 katıdır.

Karenin Çevresi: ...

Bu uzunluk aynı zamanda üçgenin de çevresine eşittir. Eşkenar üçgenin kenar uzunluğu, çevresinin üçte biridir.

Üçgenin Kenar Uzunluğu: ...

CEVAP: B

Soru 5:

Kenarlarından ikisinin uzunluğu 8 cm ve 5 cm olan bir üçgenin diğer kenarının uzunluğu aşağıdakilerden hangisi olabilir?

A) 2 cm

B) 3 cm

C) 12 cm

D) 13 cm

Çözüm:

Üçüncü kenarın uzunluğu, 8 + 5 = 13 cm'den küçük ve 8 – 5 = 3 cm'den büyüktür. Sadece C seçeneğinde verilen uzunluk bu aralıktadır.

CEVAP: C

Soru 6:

Üçgen katlayarak açıortayı kenarortayı bulma ile ilgili çıkmış soru

Çeşitkenar üçgensel bölge şeklindeki bir kağıdın AB kenarı BC kenarı ile çakışacak şekilde katlanıyor.

Kağıt tekrar açıldığında elde edilen BD katlama çizgisi, ABC üçgeninin hangi yardımcı elemanı olur?

A) Kenarortay

B) Kenar orta dikme

C) Açıortay

D) Yükseklik

Çözüm:

AB ve BD doğru parçaları arasındaki açıklıkla, BC ve BD doğru parçaları arasındaki açıklık aynı olduğu için bu doğru parçaları arasında kalan açılar da aynıdır. Dolayısıyla, BD doğru parçası, ABC üçgeninin açıortayıdır.

CEVAP: C

Soru 7:

Uzunluğu 15 cm olan [AB]’na, B noktasından dik olarak çizilen [BC]’nın uzunluğu 8 cm’dir.

Buna göre |AC| kaç santimetredir?

A) 15

B) 17

C) 19

D) 21

Çözüm:

|AC| = ... ... ... ... cm

CEVAP: B

Soru 8:

Birbirine eş 4 tane eşkenar üçgen ve bir kareden oluşan aşağıdaki şekillerden hangisi, bir kare piramidin açınımı olamaz?

Çözüm:

Kare piramitte yan yüzleri oluşturan üçgensel bölgelerin tepe noktaları ortaktır. Bu nedenle kare ile kesişen tabanların karşısındaki köşeler, tek bir noktada kesişir. C seçeneğindeki açınımdan bu şarta uyan bir geometrik cisim elde edilememektedir.

CEVAP: C

Soru 9:

Şekildeki ABC üçgeninde [AB] ⊥ [BC]'tir. |AC| = 12 cm ve sin x = ... olduğuna göre, |BC| kaç santimetredir?

A) 9

B) 8

C) 6

D) 5

Çözüm:

...

⇒ ...

⇒ ... cm

CEVAP: B

Soru 10:

Aşağıdaki grafiklerde farklı mağazalara ait yılın ilk üç ayındaki televizyon satış sayıları gösterilmiştir.

Bu grafiklerin hangisinde, satış sayılarının standart sapması diğerlerinden küçüktür?

A) 2014-2015 teog 2 standart sapma sorusu-a

B) 2014-2015 teog 2 standart sapma sorusu-b

C) 2014-2015 teog 2 standart sapma sorusu-c

D) 2014-2015 teog 2 standart sapma sorusu-d

Çözüm:

En düşük standart sapma, verilerin birbirine en yakın olduğu durumda görülür. En yakın değerleri B seçeneğinde gördüğümüz için standart sapması en düşük değerlerin B seçeneğinde olduğunu söyleyebiliriz.

CEVAP: B

Soru 11:

Şekilde B, C, D, E noktaları d doğrusunun üzerinde, A noktası ise d doğrusunun dışındadır.

Köşeleri bu noktalardan herhangi üçü olan kaç farklı üçgen çizilebilir?

A) 5

B) 6

C) 10

D) 12

Çözüm:

Bir üçgenin üç köşe noktası da aynı doğru üzerinde olamaz. Buna göre, çizilebilecek tüm üçgenlerin bir köşesi A noktası üzerindedir. Diğer 2 nokta, d doğrusu üzerindeki 4 nokta arasından ... farklı şekilde seçilebilir. Bu nedenle çizilebilecek üçgen sayısı 6'dır.

CEVAP: B

Soru 12:

A şehrinden B şehrine hava, kara, deniz ve demir yolu ile gidebilmektedir.

A şehrinden B şehrine gidecek olan Ali ve Ayşe'nin aynı ulaşım yolu ile gitme olasılığı nedir?

A) ...

B) ...

C) ...

D) ...

Çözüm:

Ali de Ayşe de 4 farklı ulaşım yolunu kullanarak A şehrinden B şehrine gidebilir. Ali ile Ayşe bağımsız hareket ettikleri için ulaşım yollarını 4 × 4 = 16 farklı şekilde seçebilirler. Bu seçimlerden 4'ünde aynı yolları kullanacakları için istenilen olasılık ...'tür.

CEVAP: C

Soru 13:

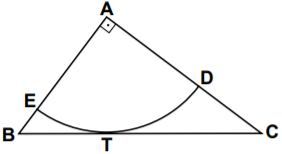
Şekildeki dik üçgende ... dir. [BC] kenarına T noktasında teğet olan A merkezli çember yayı [AC]’nı D noktasında, [AB]’nı E noktasında kesmektedir.

|DC| > |BE| olduğuna göre, ... üçgeninin açılarının ölçülerinin doğru sıralanışı aşağıdakilerden hangisidir?

A) ... < ... < ...

B) ... < ... < ...

C) ... < ... < ...

D) ... < ... < ...

Çözüm:

Bir dik üçgendeki en büyük açı, dik açıdır. Dolayısıyla, ...'nın değeri diğer iki açı ölçüsünden büyüktür. ... ve ...’den hangisinin daha büyük olduğunu bulabilmek için bu açıların karşılarındaki kenar uzunluklarını karşılaştırabiliriz.

|AE| ve |AD| uzunlukları çemberin yarıçapına eşittir. |DC| > |BE| olduğundan, |AC| uzunluğu |AB|’den büyüktür. Bu nedenle, ... ölçüsü ...'den büyüktür. Doğru sıralama aşağıdaki gibidir.

... < ... < ...

CEVAP: D

Soru 14:

Aşağıda isimleri verilen geometrik cisimlerden hangisi tabanına dik bir düzlem ile kesildiğinde ara kesit bir kare olamaz?

A) Düzgün altıgen dik prizma

B) Dik dairesel silindir

C) Kare dik piramit

D) Küp

Çözüm:

A, B ve D seçeneklerindeki geometrik cisimler, tabanlarına dik bir düzlem ile kesildiğinde karesel ara kesit elde edilebilir. Kare dik piramit ile verilen şartlara uyan bir kare elde edilemez.

Düzgün altıgen dik prizma

Dik dairesel silindirin silindirin kare kesiti-çıkmış soru

Dairesel dik silindir

Küp

CEVAP: C

Soru 15:

23, 29, a , 41 sayıları aritmetik bir dizinin ardışık dört terimi olduğuna göre, a kaçtır?

A) 31

B) 33

C) 35

D) 37

Çözüm:

Bu aritmetik dizide 2. terim 1. terimden 29 – 23 = 6 fazladır. Buna göre a sayısı da 29'dan 6 fazla olmalıdır. 29 + 6 = 35 olduğu için a = 35'tir.

CEVAP: C

Soru 16:

Verilen rampanın yüksekliği için aşağıdakilerden hangisi yapılırsa, rampanın eğimi % 20 olur?

A) 10 m azaltılırsa

B) 10 m artırılırsa

C) 20 m azaltılırsa

D) 20 m artırılırsa

Çözüm:

Eğimi % 20 olan bir rampanın yüksekliği, uzunluğunun % 20'si kadardır. 150 metre uzunluğundaki rampanın % 20'si 30 metredir. Yüksekliğin 30 m olabilmesi için şu ankine göre 10 m azaltılması gerekir.

CEVAP: A

Soru 17:

x² + 7x + 12 ifadesinin çarpanları x + a ve x + b olduğuna göre, a + b kaçtır?

A) 7

B) 8

C) 13

D) 19

Çözüm:

Verilen ifadesinin çarpanları x + 4 ve x + 3 olduğu için a + b = 7'dir.

CEVAP: A

Soru 18:

Denklemi ... olan doğrunun eğimi ... olduğuna göre, ... kaçtır?

A) –9

B) –4

C) 4

D) 9

Çözüm:

... denklemini ... formuna dönüştürelim.

...

... ...

Bu denklemin eğimi ...'dir. Bulduğumuz eğimi ...'e eşitleyerek, ...'nın değerini hesaplayabiliriz.

...

⇒ ...

CEVAP: D

Soru 19:

Aşağıdakilerden hangisi bir özdeşlik değildir?

A) 2 . (x – 3) = 3 . (x – 2)

B) (x – 3)² = x² – 6x + 9

C) x² – x = x . (x – 2)

D) x² – 4 = (x – 2) . (x + 2)

Çözüm:

A) Eşitliğin sol ve sağ tarafındaki parantezleri açalım.

Eşitliğin sol tarafı: 2 . (x – 3) = 2x – 6
Eşitliğin sağ tarafı: 3 . (x – 2) = 3x – 6

Sol ve sağ taraftaki x'lerin katsayıları aynı olmadığı için A seçeneğinde verilen eşitlik bir özdeşlik değildir.

CEVAP: A

Soru 20:

102 litre süt, şişeler tam dolacak şekilde 2 litrelik ve 3 litrelik şişelere konuyor. Toplam şişe sayısı 42 olduğuna göre, kaç tane 2 litrelik şişe kullanılmıştır?

A) 18

B) 20

C) 22

D) 24

Çözüm:

2 litrelik şişelerin sayısına x ve 3 litrelik şişelerin sayısına y diyelim.

Toplam şişe sayısı 42 olduğuna göre x + y = 42'dir. Ayrıca bu şişelerin toplam hacmi 102 litre olduğu için 2x + 3y = 102'dir. Karşımıza çıkan bu denklemler bir denklem sistemi oluşturur.

x + y = 42

2x + 3y = 102

Bu denklem sistemini çözebilmek için ilk denklemi –2 ile çarpıp, denklemleri taraf tarafa toplayalım.

–2x – 2y + 2x + 3y = –84 + 102

⇒ y = 18

y = 18 değerini ilk denklemde yerine koyarsak, x'in 24'e eşit olduğunu görebiliriz.

CEVAP: D

Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2014-2015 2.DÖNEM MAZERET-SORU VE ÇÖZÜMLERİ