BÖLÜM 1: ÇOKGENLERDE BENZERLİK
Bu bölümde, üçten fazla kenarı olan çokgenlerin benzerliği üzerine yoğunlaşıyoruz. Üçgenlerde benzerlik konusunu okumak için bu bağlantıya tıklayabilirsiniz.
Benzer çokgenlerin
- İç açıları eşittir ve
- Kenar uzunlukları arasında sabit bir oran vardır.
İki çokgenin benzer olabilmesi için eşit iç açıların ve orantılı kenar uzunluklarının aynı yönde veya ters yönde aynı sırayı takip etmesi gerekir.
Üçgenlerin aksine, iç açıların eşit olması da kenar uzunluklarının orantılı olması da, üçten fazla kenarı
olan çokgenlerin benzer olabilmesi için tek başına yeterli bir şart değildir. Üçten fazla kenarı olan çokgenlerin benzerliğini test ederken hem iç açılarına hem
kenar uzunluklarına hem de bu öğelerin sıralamasına bakmamız gerekir.
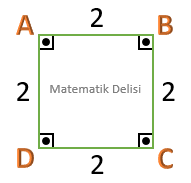
ABCD ve KLMN dörtgenlerinin iç açıları eşittir. Yalnız bu dörtgenlerin kenar uzunlukları arasında sabit bir oran bulunmamaktadır. İki kenarları aynı uzunlukta olduğu halde, diğer iki kenar uzunlukları arasındaki oran ...'dir. Bu nedenle ABCD ve KLMN dörtgenleri benzer değildir.
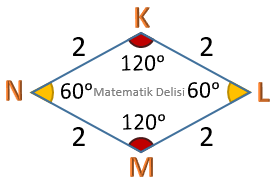
ABCD ve KLMN dörtgenlerinin kenar uzunlukları aynı olsa da iç açıları farklı olduğu için bu dörtgenler benzer değildir.
Yukarıdaki çokgenlerin iç açıları ve kenar uzunlukları eşittir. Yalnız iç açıların sıralaması farklıdır. Soldaki çokgende 270⁰'lik iç açılar D ve noktalarında birbirine komşu olduğu halde, sağdaki çokgende 270⁰'lik iç açılar arasında iki tane 90⁰'lik açı bulunmaktadır. Bu nedenle yukarıdaki çokgenler benzer değildir. Bu çokgenlerin benzer olmadığı şekillerine bakılarak da anlaşılabilir.
Benzer çokgenlerin kenar uzunlukları arasındaki sabit orana benzerlik oranı denir.
Çokgenlerde benzerlik, ~ sembolü ile gösterilir.
ACDF ~ CDEB
Yukarıdaki şekilde ACDF ve CDEB diködrtgenleri benzerdir. Bu dörtgenlerin iç açıları eşittir ve kenar uzunlukları arasında sabit bir oran bulunmaktadır. ACDF dikdörtgeninin CDEB dikdörtgenine benzerlik oranı
... ... ...'dir.
Çokgenlerin çevreleri arasındaki oran, benzerlik oranına eşittir.
