İSPAT

n basamaklı a_{n – 1}...a₂a₁a₀ sayısının 10’un kuvvetlerine göre çözümlemesini yapalım.

a_{n – 1}...a₂a₁a₀ = a_{n – 1}10^{n – 1} + ... + a₂10² + a₁10¹ + a₀10⁰

a₀ dışında kalan terimleri 10 parantezine alalım.

a_{n – 1}...a₂a₁a₀ = 10(a_{n – 1}10^{n – 2} + ... + a₂10¹ + a₁) + a₀

Parantez içerisindeki tam sayıya A dersek bu eşitlik

a_{n – 1}...a₂a₁a₀ = 10A + a₀

haline dönüşür. a₀, 10’dan küçük bir tam sayıdır. Bu nedenle yukarıdaki ifadeyi 10’a böldüğümüzde kalan a₀ olur.

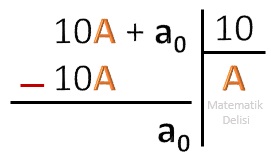
Buna göre, a_{n – 1}...a₂a₁a₀’ın 10’a kalansız bölünebilmesi için a₀’ın 0’a eşit olması gerekir.