İSPAT

En az 3 basamaklı a_{n – 1}...a₁a₀ sayısını 10’un kuvvetleri ile çözümleyelim.

a_{n – 1}...a₂a₁a₀ = a_{n – 1}10^{n – 1} + ... + a₂10² + a₁10¹ + a₀10⁰

Eşitliğin sağ tarafındaki a_{n – 1}10^{n – 1}’den a₂10²’ye kadar olan terimlerin toplamını 100 parantezine alalım.

a_{n – 1}...a₂a₁a₀ = 100(a_{n – 1}10^{n – 3} + ... + a₂) + a₁10¹ + a₀10⁰

Eşitlikte 100 yerine 4 . 25 yazalım.

a_{n – 1}...a₂a₁a₀ = 4[25(a_{n – 1}10^{n – 3} + ... + a₂)] + a₁10¹ + a₀10⁰

Bu ifadeyi kısaltmak için köşeli parantez içindeki sayıya A ve parantez dışında toplanan ifadeye B diyelim.

A = 25(a_{n – 1}10^{n – 3} + ... + a₂)

B = a₁10¹ + a₀10⁰

A ve B sayılarını eşitlikte yerlerine yazalım.

a_{n – 1}...a₂a₁a₀ = 4A + B

B’nin 4’e bölümünden kalan sayı b ise, c bir tam sayı olmak üzere bu sayıyı B = 4c + b şeklinde yazabiliriz. (1)’de B yerine 4c + b koyarsak, eşitlik

a_{n – 1}...a₂a₁a₀ = 4(A + c) + b

haline dönüşür.

A, c ve b tam sayılar olduğu için bu ifadeyi uzun bölme ile 4’e böldüğümüzde kalan b olur.

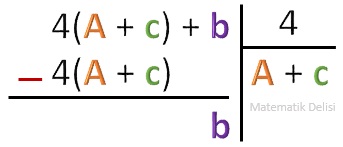
Buna göre a_{n – 1}...a₂a₁a₀ sayısının 4’e bölümünden kalan B’nin 4’e bölümünden kalana eşittir. B = 10a₁ + a₀ sayısı ise a_{n – 1}...a₂a₁a₀’ın son iki basamağını oluşturan a₁a₀ sayısına eşittir. Dolayısıyla, bir sayının 4’e tam bölünebilmesi için son iki basamağındaki sayının 4’ün tam katı veya 0 olması gerekir.

Not: Yukarıdaki çıkarımı n > 2 için yaptık. n = 1 veya n = 2 durumlarında A yerine 0 yazarak da bölünebilme kuralının doğru olduğunu gösterebiliriz.