İSPAT

n basamaklı a_{n – 1}...a₂a₁a₀ sayısını 10’un kuvvetleri ile çözümleyelim.

a_{n – 1}...a₂a₁a₀ = a_{n – 1}10^{n – 1} + ... + a₂10² + a₁10¹ + a₀10⁰

Çözümlemede a₀ dışında kalan terimleri 10 parantezine alalım.

a_{n – 1}...a₂a₁a₀ = 10(a_{n – 1}10^{n – 2} + ... + a₂10 + a₁) + a₀

= 5[2(a_{n – 1}10^{n – 2} + ... + a₂10 + a₁)] + a₀

Yukarıdaki ifadeyi kısaltmak için köşeli parantez içerisindeki tam sayıya A deyip, a_{n – 1}...a₂a₁a₀’i aşağıdaki gibi yazalım.

a_{n – 1}...a₂a₁a₀ = 5A + a₀

a₀’ın 5’e bölümünden kalan sayıya b dersek, c bir tam sayı olmak üzere a₀’ı 5c + b şeklinde yazabiliriz.

a_{n – 1}...a₂a₁a₀ = 5A + 5c + b = 5(A + c) + b

Uzun bölme ile 5(A + c) + b’nin 5’e bölümünden kalanın b olduğunu görebiliriz.

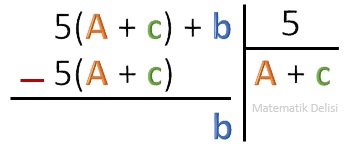
Buna göre a_{n – 1}...a₂a₁a₀ sayısının 5’e bölümünden kalanla, bu sayının birler basamağındaki rakamın 5’e bölümünden kalan aynıdır. b’nin 0’a eşit olabilmesi için a₀’ın 0 veya 5 olması gerekir.