İSPAT

n, 2’den büyük bir tam sayı olmak üzere, n basamaklı a_{n – 1}...a₃a₂a₁a₀ sayısının 10’un kuvvetleri ile çözümlemesi aşağıdaki gibidir.

a_{n – 1}...a₃a₂a₁a₀ = a_{n – 1}10^{n – 1} + ... + a₃10³ + a₂10² + a₁10¹ + a₀10⁰

Kuvveti 3 veya daha fazla olan terimleri 1000 parantezine aldığımızda bu çözümleme

a_{n – 1}...a₃a₂a₁a₀ = 1000(a_{n – 1}10^{n – 4} + ... + a₃) + a₂10² + a₁10¹ + a₀10⁰

haline dönüşür. Bu eşitlikte paranteze alınan ifadeye A ve paranteze alınmayan terimlerin toplamına B diyelim. Böylece a_{n – 1}...a₃a₂a₁a₀ sayısını daha kısa bir şekilde aşağıdaki gibi gösterebiliriz.

a_{n – 1}...a₃a₂a₁a₀ = 1000A + B

1000 yerine bu sayıya eşit olan 8 . 125 çarpımını yazalım.

a_{n – 1}...a₃a₂a₁a₀ = 8 . 125A + B           (1)

B’yi 8’e bölme işleminde bölüme c ve kalana b dersek, bu sayıyı B = 8c + b şeklinde yazabiliriz. B için bulduğumuz ifadeyi (1)’de yerine yazarsak, aşağıdaki eşitliği elde ederiz.

a_{n – 1}...a₃a₂a₁a₀ = 8 . 125A + 8c + b = 8(125A + c) + b

A, c ve b birer tam sayı olduğundan a_{n – 1}...a₃a₂a₁a₀ sayısını uzun bölme ile 8’e böldüğümüzde kalanın b’ye eşit olduğunu görebiliriz.

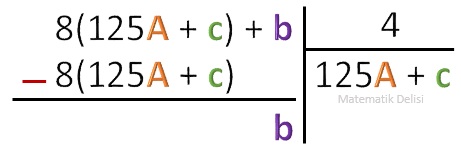
Buna göre, a_{n – 1}...a₃a₂a₁a₀ sayısının 8’e bölümünden kalan a₂10² + a₁10¹ + a₀10⁰’ın 8’e bölümünden kalan sayıya eşittir. a₂10² + a₁10¹ + a₀10⁰ ise, a_{n – 1}...a₃a₂a₁a₀’ın son üç basamağındaki a₂a₁a₀ sayısının değerine eşittir.

Özetle, bir tam sayının 8’e kalansız bölünebilmesi için son 3 basamağındaki sayının 8’e kalansız bölünebilmesi gerekir.