BÖLÜM 1: SAYI ÖRÜNTÜLERİ
Belli bir kuralı takip eden sayı veya şekil dizilerine örüntü denir.
Sayı ve şekil örüntüleri adımlar halinde ilerler. Yukarıda, bir sayı örüntüsünün ilk 4 adımı ve bir şekil örüntüsünün ilk 3 adımı gösterilmiştir.
SAYI ÖRÜNTÜLERİ
Sayılardan oluşan örüntülere sayı örüntüsü adı verilir. Bu örüntülerdeki sayılar belli bir kurala göre dizilir.
Aşağıdaki dizilerin her biri birer sayı örüntüsüdür.
- 1, 5, 9, 14, ...
- 2, 4, 6, 8
- 100, 150, 200, 250
- 10000, 10001, 10002, ...
- 512, 509, 506, ...
- 5412, 4412, 3412, ...
Bu dizilerin tamamı belli kurallara göre dizilmiş sayılardan oluşur.
Sayı örüntüsündeki sayılardan her birine terim denir.
- Birinci adımdaki sayıya birinci terim,
- İkinci adımdaki sayıya ikinci terim,
- Üçüncü adımdaki sayıya üçüncü terim vb.
1, 5, 9, 14...
Yukarıdaki örüntünün
- birinci terimi 1;
- ikinci terimi 5;
- üçüncü terimi 9; ve
- dördüncü terim 14’tür.
ÖRÜNTÜDEKİ TERİM SAYISI
Bazı örüntülerde sonlu sayıda terim olduğu halde, bazılarındaki terim sayısı sonsuzdur.
Bir sayı örüntüsünün sonundaki “...” işareti, terimlerin aynı kurala göre devam ettiğini gösterir.
İkinci örüntünün 150., 500. veya 5 000 000. terimlerini bulabiliriz.
ÖRÜNTÜDEKİ TERİMLERİ BULMA
Şimdi ilk terimi ve kuralı verilen bir örüntünün adımlarını nasıl bulacağımızı öğrenelim.
İlk terimi 2 olan ve her adımda 3 artan bir sayı örüntüsün terimlerini bulalım.
| 1. ADIM | |
| 2 | İlk terimi örüntüye yazalım. |
| 2. ADIM | |
| 2, 5 | Kurala göre, ikinci terim ilkinden 3 fazla olmalıdır. 2 + 3 = 5 olduğundan, ikinci terim 5’e eşittir. |
| 3. ADIM | |
| 2, 5, 8 | Yine aynı kurala göre üçüncü terim ikinciden 3 fazla olmalıdır. 5 + 3 = 8 olduğundan, üçüncü terim 8’dir. |
| 4. ADIM | |
| 2, 5, 8, 11 | Dördüncü terim, üçüncüden 3 fazla olmalıdır. 8 + 3 = 11 olduğundan, dördüncü terim 11’dir. |
Bu şekilde devam ederek, istediğimiz adıma kadar ilerleyebiliriz.
2, 5, 8, 11, 14, 17, ...
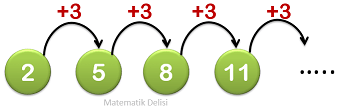
Örüntünün kuralı tek başına bir örüntüyü belirlemede yeterli değildir. Örüntüyü belirleyen diğer bir faktör de ilk terimdir.
Aşağıdaki örüntülerin tümünde, her terim bir öncekinden 3 fazladır.
- 2, 5, 8, 11, ....
- 1, 4, 7, 10, ....
- 3, 6, 9, 12, ....
Aynı kural uygulandığı halde yukarıdaki örüntüler farklıdır. Bunun nedeni, ilk terimlerinin farklı olmasıdır.
İlk terimi ve kuralı verilen aşağıdaki örüntülerin ilk 5 terimini bulun.
| Açıklama | 1. TERİM | 2. TERİM | 3. TERİM | 4. TERİM | 5. TERİM |
| Açıklama | 1. TERİM | 2. TERİM | 3. TERİM | 4. TERİM | 5. TERİM |
| İlk terimi 5 ve her adımda 10 artıyor. | 5 | 15 | 25 | 35 | 45 |
| İlk terimi 1000 ve her adımda 120 artıyor. | |||||
| İlk terimi 3 ve her adımda 1000 artıyor. | |||||
| İlk terimi 103 ve her adımda 12 artıyor. | |||||
| İlk terimi 8 ve her adımda 3 artıyor. | |||||
| İlk terimi 120 ve her adımda 1 artıyor. |
AZALAN SAYI ÖRÜNTÜLERİ
Bir sayı örüntüsü her adımda artmak zorunda değildir. Bazı örüntülerdeki terimler adım adım azalır.
İlk terimi 120 olan ve her adımda 10 azalan sayı örüntüsünün terimlerini bulalım.
| 1. ADIM | |
| 120 | İlk terimi yazalım. |
| 2. ADIM | |
| 120, 110 | Örüntünün kuralına göre, bir sonraki terim 120’den 10 eksik olmalıdır. 120 – 10 = 110 olduğu için ikinci terim 110’dur. |
| 3. ADIM | |
| 120, 110, 100 | Kuralı bir kez daha uyguladığımızda, üçüncü terimin 110 – 10 = 100 olduğunu görebiliriz. |
| 4. ADIM | |
| 120, 110, 100, 90 | 100 – 10 = 90 olduğundan dördüncü terim 90’dır. |
Bu şekilde devam ederek, örüntünün diğer adımlarını da bulabiliriz.
120, 110, 100, 90, 80, 70, ...
İlk terimi ve kuralı verilen aşağıdaki örüntülerin ilk 5 terimini bulun.
| Açıklama | 1. TERİM | 2. TERİM | 3. TERİM | 4. TERİM | 5. TERİM |
| Açıklama | 1. TERİM | 2. TERİM | 3. TERİM | 4. TERİM | 5. TERİM |
| İlk terimi 50 ve her adımda 2 azalıyor. | 50 | 48 | 46 | 44 | 42 |
| İlk terimi 1000 ve her adımda 120 azalıyor. | |||||
| İlk terimi 30 ve her adımda 1 azalıyor. | |||||
| İlk terimi 98 ve her adımda 12 azalıyor. | |||||
| İlk terimi 17 ve her adımda 3 azalıyor. | |||||
| İlk terimi 39 ve her adımda 7 azalıyor. |
SONLU SAYIDA TERİMİ OLAN ÖRÜNTÜLER
Önceki iki örnekte, örüntünün terim sayısında herhangi bir kısıtlama yoktu. Şimdi de, sonlu sayıda terimi olan bir sayı örüntüsü görelim.
İlk terimi 1001 olan ve her adımda 100 artan üç terimli bir sayı örüntüsü oluşturalım.
| 1. ADIM | 1001 | İlk terimi yazalım. |
| 2. ADIM | 1001, 1101 | İkinci terimi bulmak için ilkine 100 ekleyelim: 1001 + 100 = 1101 |
| 3. ADIM | 1001, 1101, 1201 | Son terim için ise, ikinci terime 100 ekleyelim: 1101 + 100 = 1201 |
Bu örüntü sadece üç terimden oluşmaktadır. Bu nedenle, dördüncü adıma geçmeyiz.
1001, 1101, 1201
