BÖLÜM 3: İKİ BASAMAKLI SAYILARA BÖLME

Bu bölümde, üç veya dört basamaklı bir sayıyı iki basamaklı bir sayıya nasıl bölebileceğimizi öğreniyoruz.

ÖRNEK:

716’yı 12’ye bölelim.

	Bu işlemdeki bölünen 716 ve bölen 12'dir.
	Bölünenin en yüksek basamağındaki rakam olan 7 ile başlayalım. 7, 12’den küçük olduğu için bölünenin bir sonraki basamağını da kullanalım. 71 sayısı 12’den büyük olduğu için bölmeye bu sayıyla devam edelim.
	12’yi en fazla 5 ile çarptığımızda 71 veya daha küçük bir sayı elde ederiz.
	5 × 12 = 60'tır. 71’in altına 60 yazalım.
	Çıkarma işlemini yapalım. 71 – 60 = 11
	Bölme işleminde 716’nın birler basamağındaki rakamı henüz kullanmadık. Bu basamaktaki 6'yı 11’in sağına yazalım.
	12’yi en fazla 9 ile çarptığımızda 116 veya daha küçük bir sayı elde edeceğimiz için bölüme 9 yazalım.
	9 × 12 = 108 olduğundan 116’nin altına 108 yazalım.
	Çıkarma işlemini yapalım. 116 – 108 = 8

716’nın kullanmadığımız bir rakamı kalmadığı için işlemi sonlandıralım. Bu işlemdeki bölüm 59 ve kalan 8'dir.

3 VEYA 4 BASAMAKLI SAYILARIN 2 BASAMAKLI SAYILARA BÖLÜMÜYLE İLGİLİ FAZLADAN 50 ÖRNEK İÇİN TIKLAYIN!

Bölüme hangi rakamı yazacağımızı bulabilmek için böleni en fazla kaç ile çarptığımızda, böleceğimiz sayıya eşit veya daha küçük bir sonuç elde edebileceğimizi hesaplıyorduk. Yalnız bunu yaparken çok kolay olmayan işlemlerle de karşılaşabiliriz. Böyle durumlarda bir tahminde bulunup, çarpım sonucunda çıkan sayıya göre tahminimizi yineleyebiliriz.

Örneğin, yukarıdaki bölme işleminde, 12'yi en fazla kaç ile çarptığımızda 71 veya daha küçük bir sayı elde edeceğimizi bulmuştuk. Bu sayının kaç olduğunu o an çıkaramazsak, bir tahminde bulunabiliriz.

Tahminimizin 6 olduğunu düşünelim. 6 × 12 = 72 sonucu 71’den büyük olduğu için tahminimizi düşürmemiz gerekir. Aradaki fark 12’den küçük olduğu için tahminimizi 1 azaltmamız yeterlidir.
Tahminimiz 4 olduğunda ise çarpım sonucu 4 × 12 = 48 çıkar. 71'den bu sonucu çıkardığımızda 12'den büyük bir sayı elde ederiz. Çıkarma işleminin sonucu her zaman bölenden küçük olması gerektiği için bu durumda da tahminimizi arttırmamız gerekir.

BÖLME HESAPLAMA ARACI
👉🏻Aracı kullanmak için tıklayın👈🏻

ÖRNEK:

1866’yı 41’e bölelim.

	Bu işlemdeki bölünen 1866 ve bölen 41'dir.
	Bölünenin en yüksek basamağındaki rakam olan 1’den başlayalım. 1, 41’den küçük olduğu için bölünenin bir sonraki basamağını olan 8’i de kullanmamız gerekir. Yalnız, yeni oluşturduğumuz 18 sayısı da 41’den küçüktür. Bu nedenle, sonraki rakam olan 6’yı da kullanmamız gerekir. Böylece, böleceğimiz sayı 186 haline dönüşür. 186 sayısı 41’den büyük olduğu için yeni rakamları işleme dâhil etmeyi bırakıp, bölmeye devam edelim.
	41’i en fazla 4 ile çarptığımızda 186 veya daha küçük bir sayı elde ederiz. Bu nedenle bölüme 4 rakamını yazalım.
	4 × 41 = 164 olduğu için 186’nın altına 164 yazalım.
	Çıkarma işlemini gerçekleştirelim. 186 – 164 = 22
	1866’nın birler basamağındaki 6 dışında kalan tüm rakamlarını kullandık. 6’yı 22’nin sağına yazalım.
	41'i en fazla 5 ile çarptığımızda 226 veya daha küçük bir sayı elde edeceğimizden, bölüme 5 rakamını yazalım.
	5 × 41 = 205 olduğu için 226’nın altına 205 yazalım.
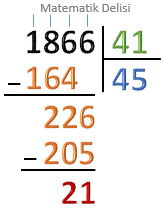
	Çıkarma işlemini yapalım. 226 – 205 = 21

1866’nın kullanmadığımız bir rakamı kalmadığı için işlemi sonlandırabiliriz. Bu işlemde bölüm 45 ve kalan 21'dir.

3 VEYA 4 BASAMAKLI SAYILARIN 2 BASAMAKLI SAYILARA BÖLÜMÜYLE İLGİLİ FAZLADAN 50 ÖRNEK İÇİN TIKLAYIN!

ÖRNEK:

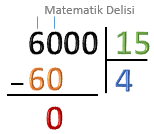
6000’i 15’e bölelim.

	Bu işlemdeki bölünen 6000 ve bölen 15’tir.
	Bölünenin en yüksek basamağındaki rakam olan 6’dan başlayalım. 6 < 15 olduğundan bir sonraki basamak olan 0’ı da kullanmamız gerekir. 60 > 15 olduğu için bölmeye devam edelim.
	15’i en fazla 4 ile çarptığımızda 60 veya daha küçük bir sayı elde ederiz. Bölüme 4 yazalım.
	4 × 15 = 60 olduğu için bölünenin altına 60 yazalım.
	Çıkarma işlemini yapalım. 60 – 60 = 0
	6000’in kullanmadığımız bir sonraki rakamı olan 0’ı alttaki 0’ın yanına yazalım. Fakat bu sayının değeri yine 0’a eşittir ve 15’ten küçük olduğu için bölüme 0 yazıp, bir sonraki basamağa geçelim.
	Bir sonraki basamaktaki rakamın da 0 olduğunu görüyoruz. 00’ın sağına bir tane daha 0 eklediğimizde 000 sayısını elde ederiz. Fakat bu sayının da değeri 0’dır. 15’ten küçük bir sayıyla karşılaştığımız için bölüme bir tane daha 0 eklememiz gerekir.