Bu sayıları alt alta çarpım halinde yazalım.

387'yi alttaki sayının birler basamağı ile çarpalım.

387'nin birler basamağı

4 × 7 = 28

8’i alta yazalım. Elde var 2.

387'nin onlar basamağı

4 × 8 = 32

Birler basamağından gelen eldeyi ekleyelim.

32 + 2 = 34

4’ü alta yazalım. Elde var 3.

387'nin yüzler basamağı

4 × 3 = 12

12 + 3 = 15

15’i alta yazalım.

387'yi alttaki sayının onlar basamağı ile çarpalım.

387'nin birler basamağı

1 × 7 = 7

7’yi alta yazalım. Elde yok.

387'nin onlar basamağı

1 × 8 = 8

8’i alta yazalım. Elde yok.

387'nin yüzler basamağı

1 × 3 = 3

3’ü alta yazalım.

387'yi alttaki sayının yüzler basamağı ile çarpalım.

387'nin birler basamağı

6 × 7 = 42

2’yi alta yazalım. Elde var 4.

387'nin onlar basamağı

6 × 8 = 48

Birler basamağından gelen eldeyi ekleyelim.

48 + 4 = 52

2’yi alta yazalım. Elde var 5.

387'nin yüzler basamağı

6 × 3 = 18

Onlar basamağından gelen eldeyi ekleyelim.

18 + 5 = 23

23’ü alta yazalım.

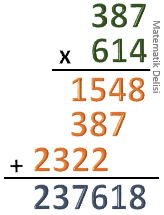
Son adımda, yazılmayan basamakları 0 kabul ederek, üç çarpımı alt alta topluyoruz.

• Birler basamağı: 8 + 0(boşluk) + 0(boşluk) = 8. 8’i alta yazalım. Elde yok.
• Onlar basamağı: 4 + 7 + 0(boşluk) = 11. 1’i alta yazalım. Elde var 1.
• Yüzler basamağı: 5 + 8 + 2 + 1 = 16. 6’yı alta yazalım. Elde var 1.
• Binler basamağı: 1 + 3 + 2 + 1 = 7. 7’yi alta yazalım. Elde yok.
• On binler basamağı: 0(boşluk) + 0(boşluk) + 3 = 3. 3’ü alta yazalım. Elde yok.
• Yüz binler basamağı: 0(boşluk) + 0(boşluk) + 2 = 2. 2’yi alta yazalım.