BÖLÜM 1: İÇ AÇILARINA GÖRE ÜÇGENLER
ÜÇGENİN İÇ AÇILARI
Üçgenin iç açıları toplamı
...’dir.
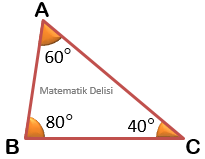
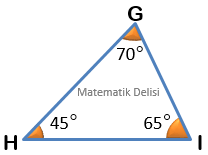
Yukarıdaki üçgenlerin iç açılarını topladığımızda, tüm üçgenler için bu toplamın ... olduğunu görebiliriz.
- 1. Üçgen: ... ...
- 2. Üçgen: ... ...
- 3. Üçgen: ... ...
İç açılarından ikisi verilen üçgenlerin, üçüncü iç açılarını bulun.
a) ..., ..., ...... ......
b) ..., ..., ...............
c) ..., ..., ... ............
ç) ..., ..., ...............
d) ..., ..., ... ............
Üçgenleri, iç açılarına ve kenar uzunluklarına göre sınıflandırabiliriz.
İÇ AÇILARINA GÖRE ÜÇGENLER
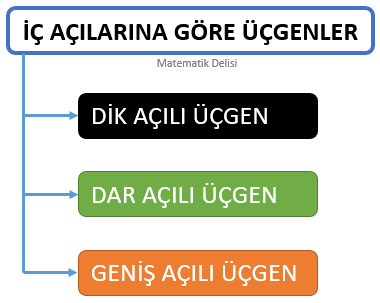
İç açılarına göre üçgenler üçe ayrılır.
- Dik açılı üçgenler,
- Dar açılı üçgenler ve
- Geniş açılı üçgenler.
DİK AÇILI ÜÇGENLER
İç açılarından biri ... olan üçgenlere dik üçgen ismi verilir.
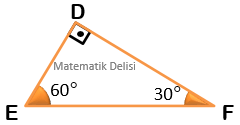
Açılardan biri ... olduğundan, yukarıdaki üçgenler dik üçgendir.
DAR AÇILI ÜÇGENLER
Tüm iç açıları ...’den
küçük olan üçgenlere dar açılı üçgen ismi verilir.
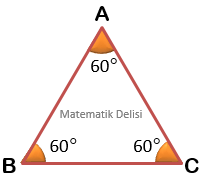
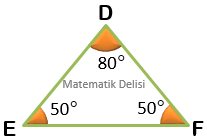
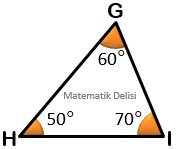
Yukarıda dar açılı üçgenler görüyoruz. Bu üçgenlerin tüm iç açıları ...’den küçüktür.
GENİŞ AÇILI ÜÇGENLER
İç açılarından biri ...’den
büyük olan üçgenlere geniş açılı üçgen denir.
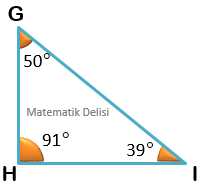
Yukarıda geniş açılı üçgenler görüyoruz. Bu üçgenlerin iç açılarından biri ...’den büyüktür.
Bir üçgen ya dik, ya dar, ya da geniş açılıdır.
