BÖLÜM 2: KENAR UZUNLUKLARINA GÖRE ÜÇGENLER
Kenar uzunluklarına göre üçgenler üçe ayrılır.
- Eşkenar üçgenler,
- İkizkenar üçgenler ve
- Çeşitkenar üçgenler.
EŞKENAR ÜÇGENLER
Tüm kenar uzunlukları birbirine eşit olan üçgenlere eşkenar üçgen ismi verilir.
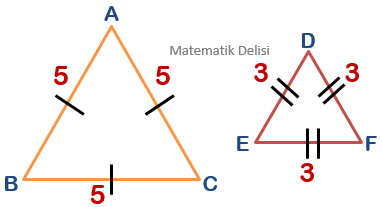
Yukarıdaki eşkenar üçgenlerin tüm kenar uzunlukları birbirine eşittir.
Kenar uzunluklarının eşit olduğunu göstermek için bu kenarların üzerine aynı işareti
(tek çizgi, çift çizgi vs.) koyarız.
Eşkenar üçgenin iç açılarından her biri
...’dir. Kenar uzunlukları verilmemiş olsa da, bir üçgenin iç açılarından her biri
... ise, bu üçgenin bir eşkenar üçgendir.
Yukarıdaki üçgende |AC| uzunluğunu bulalım.
... ... ...’dir.
Üçgenin iç açıları toplamı ... olduğundan,
... ... ...'dir.
ABC üçgeninin tüm iç açıları ... olduğu için bu üçgen bir eşkenar üçgendir. Bir eşkenar üçgende tüm kenar uzunlukları eşit olduğundan, |AC| = |AB| = 8'dir.
İKİZKENAR ÜÇGENLER
İkizkenar üçgenin iki kenar uzunluğu birbirine eşittir.
Yukarıdaki üçgenler ikizkenardır.
İkizkenar bir üçgende, eşit uzunluktaki kenarların üçüncü kenarla yaptığı açılar
birbirine eşittir. Bunun tersi de doğrudur. İki açısı eşit olan bir üçgen, ikizkenar üçgendir.
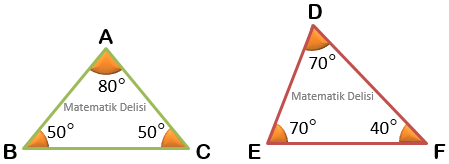
Yukarıdaki üçgenlerin iç açılarından ikisi eşit olduğu için bu üçgenler ikizkenardır.
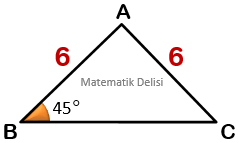
Yukarıdaki üçgenin ... açısını bulalım.
|AB| = |AC| olduğu için bu üçgen bir ikizkenar üçgendir. Buna göre ... ve ... açıları eşittir.
...
Üçüncü açıyı bulabilmek için ... ve ... açılarını toplar, bulduğumuz sonucu ...'den çıkarırız.
... ... ...
⇒ ... ... ...
ÇEŞİTKENAR ÜÇGENLER
Tüm kenar uzunlukları birbirinden farklı olan üçgenlere çeşitkenar üçgen denir.
Yukarıdaki üçgenlerin kenar uzunlukları birbirinden farklı olduğu için bu üçgenler çeşitkenardır.
Çeşitkenar üçgenlerin iç açıları birbirinden farklıdır.
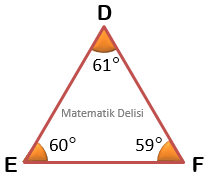
Yukarıdaki üçgenlerin iç açıları farklı olduğundan bu üçgenler çeşitkenardır.
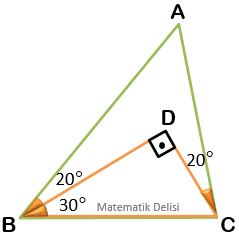
Yukarıdaki ABC üçgeninin, açılarına ve kenar uzunluklarına göre çeşidini bulalım.
BDC üçgeninde verilen açıların toplamı ... ...’dir. Bir üçgende iç açıların toplamı ... olduğundan,
... ... ...'dir.
ABC üçgeninde ise,
- ... ... ... ve
- ... ... ...'dir.
ABC üçgeninin üçüncü açısını bulabilmek için ... ve ... açılarını ...'den çıkarırız.
... ... ...
Buna göre, ABC üçgeninin iç açıları ..., ... ve ...’dir. Bu üçgenin iç açılarından ikisi birbirine eşit olduğu için ABC bir ikizkenar üçgendir.
Ayrıca, tüm iç açıları ...’den küçük olduğu için ABC üçgeni dar açılı üçgendir.
