LİSELERE GİRİŞ SINAVI-ÖRNEK SORULAR

KASIM 2019-LGS MATEMATİK-ÖRNEK SORULARININ ÇÖZÜMLERİ

---

Bu sayfada, MEB’in yayınladığı 2019-2020 LGS Kasım ayı örnek sorularının çözümlerini bulabilirsiniz. Soruları görmek için bu bağlantıyı tıklayabilirsiniz.

DİĞER AYLARIN ÖRNEK SORULARI VE ÇÖZÜMLERİ İÇİN TIKLAYIN!

ÖRNEK SORU 1’in Çözümü

Karenin alanı:

Karenin alanı kenar uzunluğunun karesine eşittir.

Karenin alanı = ... ... ... cm²

Dikdörtgenin alanı:

% 40'ı 20 cm² olan bir dikdörtgenin alanının tamamı ... cm²'dir.

Dikdörtgenin kenar uzunlukları:

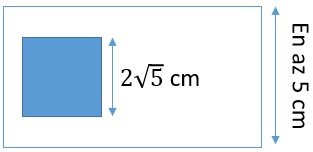
Dikdörtgen şeklindeki kimliğin kenar uzunluklarını bulabilmek için çarpımı 50 olan tam sayılara bakacağız. Yalnız fotoğrafın kimlikten taşmamasaı için bu tam sayıların ...'ten büyük olması gerekir. ...'den büyük en küçük tam sayı 5'tir. Buna göre, kimliğin kenar uzunluklarının santimetre cinsinden 5 veya daha büyük olması gerekir. 50'nin 5 veya daha büyük çarpanları (5, 10, 25 ve 50) arasından çarpımları 50'ye eşit olan tek sayı ikilisi (5, 10)'dur. Dolayısıyla, kimliğin kenar uzunlukları 5 cm ve 10 cm olmalıdır.

Dikdörtgenin çevresi:

Sırasıyla, kısa ve uzun kenarları, 5 cm ve 10 cm uzunluğunda olan bir dikdörtgenin çevresi 30 cm'dir.

2 . (5 + 10) = 30 cm

CEVAP: B

ÖRNEK SORU 2’nin Çözümü

3, 5, 7, 9 ve 11 sayılarından aralarında asal olmayanlar 3 ve 9'dur. Sorudaki kurala göre, 3 ile 9'un birbiri ile bağlantılı karelere yazılmaması gerekir. Sarı kare, diğer tüm karelere bağlı olduğundan 3 veya 9 sayılarından herhangi biri bu kareye yazılamaz. Sarı kareye diğer sayılardan herhangi biri yazıldığında, 3 ile 9 sayıları bağlantısız bir şekilde yerleştirilebilir. Buna göre sarı kareye gelebilecek sayıların toplamı 23'tür.

5 + 7 + 11 = 23

CEVAP: C

ÖRNEK SORU 3’ün Çözümü

• 1400 = 1,4 . 10³ ve
• 1050 = 1,05 . 10³'tür

Bu sayıların çarpımı 1,47 . 10⁶ yapar.

1,4 . 10³ . 1,05 . 10³ = 1,47 . 10^{3 + 3} = 1,47 . 10⁶

CEVAP: C

ÖRNEK SORU 4’ün Çözümü

Mama kaplarının bir noktada aynı hizaya gelebilmesi için bu noktanın başlangıç noktasına olan uzaklığının hem 12 hem de 15'in tam katı olması gerekir.

EKOK(12, 15) = 2 . 2 . 3 . 5 = 60'tır. 180 metrelik yolun başına ve sonuna birer tane gelecek şekilde 60'ar metre arayla 180 ÷ 60 + 1 = 4 noktada mama kapları aynı hizaya gelir.

Soruda anlatılana göre, muhtar bu noktaların her birine, iki kaldırımda da birer tane olacak şekilde toplam 2 su kabı koyuyor. Buna göre, kaldırımlara koyduğu toplam su kabı sayısı 4 × 2 = 8'dir.

CEVAP: B

ÖRNEK SORU 5’in Çözümü

Robot, bitiş noktasına ulaşabilmek için

• 4 birim sağa ve
• 3 birim yukarı

doğru hareket etmelidir. Buna göre, verilen kareköklü sayılardan birine en yakın doğal sayının 4 ve diğerine en yakın doğal sayının 3 olması gerekir.

• 4 birimlik mesafeyi sağa doğru gidebilmesi için 4'e yakın olan kareköklü sayının ...'dan büyük;
• 3 birimlik mesafeyi yukarı yönlü gidebilmesi için 3'e yakın olan kareköklü sayının ...'dan küçük

olması gerekir. Bu şartları sağlayan sayılar D seçeneğinde verilmiştir.

CEVAP: D

ÖRNEK SORU 6’nın Çözümü

Bu soruda ...'den büyük en küçük doğal sayı ile ...'den küçük en büyük doğal sayının çarpımı sorulmaktadır.

• 157'den büyük en küçük tam kare sayı 169'dur. Buna göre, yeşil bölgeden elde edilecek sayı ...'tür.
• 50'den küçük en büyük tam kare sayı 49'dur. Buna göre, turuncu bölgeden elde edilecek sayı ...'dir.

Yukarıdaki çıkarımlara göre, Doruk'un aldığı puan 13 . 7 = 91'dir.

CEVAP: B

ÖRNEK SORU 7’nin Çözümü

• ... ... ve
• ... ...'dir.

Buna göre, bayrağın genişliği

... ... ... ... metredir.

Genişliğinin 1,5 katı olduğuna göre bu bayrağın boyu ... metredir.

Dikdörtgen şeklindeki bayrağın bir yüzünün alanı, eni ile boyunun çarpılmasıyla bulunabilir.

Alan = ... ... ... m²'dir.

CEVAP: D

ÖRNEK SORU 8’in Çözümü

*Tabeladaki sayı 1 saniye boyunca değişmediği için Kerem'in tabelada 10 yazısını görmesi, kırmızı ışığın yanmasına 9 ile 10 saniye arasında bir zaman kaldığını gösterir. 2 saniye kala karşıya ulaştığına göre, Kerem'in yolu geçmesi 10 – 2 = 8 ile 9 – 2 = 7 saniye arasında bir zaman almıştır.

Saniyede 1 m sabit hızla giden Kerem, bu zaman aralığında 7 m ile 8 m arasında bir uzaklık kateder. Buna göre, yolun uzunluğunun 7 m ile 8 m arasında olması gerekir.

Seçeneklerdeki sayıları karekök içerisine alalım.

A) ... ...

B) ... ...

C) ... ...

D) ... ...

... ile ... arasında olan tek sayı A seçeneğinde verilmiştir.

Not: *Tabeladaki sayının 2'den 1'e döndüğü anı düşünelim. Biz burada, bu andan tam bir saniye sonra kırmızı ışığın yandığını düşünüyoruz. Eğer kırmızı ışık o anda yanmıyor ve bir saniye boyunca da tabelada 0 sayısı görünüyorsa, yaya geçidinin uzunluğu B veya C seçenekleri olabilir. Burada kritik olan nokta, bir saniyelik periyodun başında mı yoksa sonunda mı tabeladaki sayının doğruyu gösterdiğidir. Bu durumu netleştirmek adına, soru kökünde konuyla ilgili daha fazla bilgi verilmesi gerektiğini düşünüyoruz.

CEVAP: A

ÖRNEK SORU 9’un Çözümü

Taburenin en uzun ve en kısa halleri arasındaki boy farkı 60 – 45 = 15 cm'dir. Bir turda ... cm fark ettiğine göre, en kısa halinden en uzun haline getirilebilmesi için bu taburenin ... defa döndürülmesi gerekir.

...

75'ten küçük en büyük tam kare sayı 64 olduğundan, Eylül bu tabureyi en çok ... tam tur döndürmüştür.

CEVAP: C

ÖRNEK SORU 10’un Çözümü

Grafiklerde ortak meyve olmadığı için daire grafiğindeki "Diğer meyveler" kısmı kivi, mandalina, ayva, elma ve varsa grafiklerde ismi geçmeyen başka meyveleri de içerir. Buna göre, daire grafiğindeki

360° – (90° + 30° + 30°) = 210°'lik

kısım 10 + 45 + 15 + 35 = 105 kg kivi, mandalina, ayva ve elma ile eğer varsa tablolarda ismi geçmeyen diğer meyvelerin toplam kütlesini gösterir. Buna göre, 1 kg meyve en fazla 210 ÷ 105 = 2° ile gösterilmiştir. Daire grafiğinde 90°'lik kısımda gösterildiğine göre, günlük satılan portakal miktarı en az 90 ÷ 2 = 45 kg'dır.

CEVAP: C