Sınıf 8 ➤ TESTLER ➤ KONU 1 ➤ ÇÖZÜMLÜ KONU TESTİ

SÜRE

15:00

ÇARPAN NEDİR?

ÇÖZÜMLÜ KONU TESTİ

SORU 1
Çarpanlar ve Katlar Testi-Dikdörtgen Testi

Yukarıdaki şekilde, BCDE bir kare ve ABEF bir dikdörtgendir. Kenar uzunlukları metre cinsinden tam sayı olan ABEF dikdörtgeninin alanı 28 m2'dir.

Buna göre, ACDF dikdörtgeninin alanı aşağıdakilerden hangisi olamaz?

ACDF dikdörtgeninin alanı, ABEF ile BCDE'nin toplam alanına eşittir. |BE| uzunluğuna x dersek BCDE karesinin alanı x2 metrekare olur. ABEF dikdörtgeninin alanı 28 m2 olduğu için metrekare cinsinden toplam alan 28 + x2'dir.

|BE| = x uzunluğu ABEF dikdörtgeninin de kenar uzunluklarından biridir. ABEF'nin kenar uzunlukları tam sayı olduğuna göre bu sayı 28'in çarpanlarından biri olmalıdır. 28'in çarpanları 1, 2, 4, 7, 14 ve 28'dir.

  • x = 1 için toplam alan 28 + 12 = 29 m2,
  • x = 7 için toplam alan 28 + 72 = 77 m2 ve
  • x = 14 için toplam alan 28 + 142 = 224 m2 olur.

Çarpanlardan hiçbiri 64 m2 sonucunu vermediği için cevap B'dir.

CEVAP: B

SORU 2

2, 4, 15, ?

Yukarıdaki sayı dizisinde, her terimin bir öncekinden bir fazla çarpanı vardır.

? yerine aşağıdaki sayılardan hangisi gelebilir?

15'in çarpanları 1, 3, 5 ve 15'tir. 15'in 4 çarpanı olduğuna göre ? yerine 5 çarpanı olan bir sayı gelmelidir.

  • 16'nın çarpanları: 1, 2, 4, 8 ve 16 ⇒ (5 çarpan)
  • 18'in çarpanları: 1, 2, 3, 6, 9 ve 18 ⇒ (6 çarpan)
  • 25'in çarpanları: 1, 5 ve 25 ⇒ (3 çarpan)
  • 28'in çarpanları: 1, 2, 4, 7, 14 ve 28 ⇒ (6 çarpan)

Seçenekler içinde 5 çarpanı olan tek sayı 16'dır.

CEVAP: A

SORU 3

Ayrıt uzunlukları a, b ve c olan bir dikdörtgenler prizmasının hacmi a . b . c'ye ve farklı yüzlerinin alanları a . b, b . c ve a . c'ye eşittir.

Çarpanlar ve Katlar Testi-Dikdörtgenler Prizması

Yukarıdaki dikdörtgenler primasının ayrıt uzunlukları metre cinsinden tam sayıdır ve hacmi 12 m3'tür.

Bu dikdörtgenler prizmasının en küçük yüzünün alanı en fazla kaç metrekare olabilir?

Bu dikdörtgenler prizmasının ayrıt uzunlukları, çarpımları 12 olan tam sayılardır. Bu uzunluklar metre cinsinden

  • 1, 1 ve 12,
  • 1, 2 ve 6,
  • 1, 3 ve 4 veya
  • 2, 2 ve 3

olabilir.

  • Ayrıt uzunlukları 1 m, 1 m ve 12 m ise yüzey alanları 1 m2, 12 m2 ve 12 m2 olur. Bu alanlardan en küçüğü 1 m2'dir.
  • Ayrıt uzunlukları 1 m, 2 m ve 6 m ise yüzey alanları 2 m2, 6 m2 ve 12 m2 olur. Bu alanlardan en küçüğü 2 m2'dir.
  • Ayrıt uzunlukları 1 m, 3 m ve 4 m ise yüzey alanları 3 m2, 4 m2 ve 12 m2 olur. Bu alanlardan en küçüğü 3 m2'dir.
  • Ayrıt uzunlukları 2 m, 2 m ve 3 m ise yüzey alanları 4 m2, 6 m2 ve 6 m2 olur. Bu alanlardan en küçüğü 4 m2'dir.

Buna göre en küçük yüzün alanı en fazla 4 m2 olabilir.

CEVAP: C

SORU 4
Çarpan Nedir- Test-Çubuk Sorusu

Kalınlığı ihmal edilebilecek kadar küçük olan 36 dm uzunluğundaki bir tahta çubuk, uzunlukları desimetre cinsinden tam sayı olan 4 veya daha fazla parçaya bölünecektir. Daha sonra bu parçalardan 4'ü birleştirilerek kare şeklinde bir resim çerçevesi yapılacaktır.

Çarpan Nedir- Test-Çerçeve Sorusu

Bu şekilde yapılabilecek çerçevelerden en büyüğü ile en küçüğünün çevrelediği alanlar arasındaki fark kaç desimetrekaredir?

36'nın çarpanları 1, 2, 3, 4, 6, 9, 12, 18 ve 36'dır. Tahta çubuk 4, 6, 9, 12, 18 veya 36 eşit parçaya bölünecektir. 4 eşit parçaya bölünürse, parçalardan her birinin uzunluğu 9 dm ve bu parçalarla yapılan çerçevenin içinde kalan alan 9 . 9 = 81 dm2 olur. Aynı çubuk 36 eşit parçaya bölünürse, parçalardan her birinin boyu 1 dm ve çerçevenin içinde kalan alan 1 . 1 = 1 dm2 olur. En büyük ve en küçük alanlar arasındaki fark 81 – 1 = 80 dm2'dir.

CEVAP: C

SORU 5
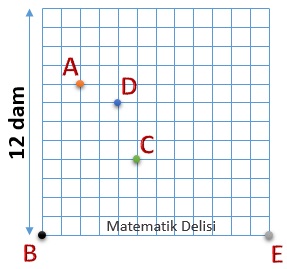
Çarpan Testi-Alan Sorusu

Ali, Ahmet, Ayşe ve Aylin kardeşler, yukarıda gösterilen araziyi ortaklaşa satın almışlardır. Eşit miktarda para verdikleri için kardeşlerin arazideki payları eşittir.Kare şeklindeki bu arazinin bir kenarı 12 dekametre uzunluğundadır.

Kardeşleri Ali'nin payına düşen kısmın boyutlarını ve arazinin hangi bölümünde olacağını seçmesine imkân tanımışlar, yalnız seçeceği kısımla ilgili aşağıdaki maddeleri şart koşmuşlardır.

  • Dikdörtgen şeklinde olacak.
  • Tabanı BE doğru parçasına paralel olacak.
  • Eni ve boyu dam cinsinden tam sayı olacak.

Buna göre, arazi üzerinde gösterilen noktalardan hangisi, Ali'nin seçeceği dikdörtgen şeklindeki arazinin sol alt köşesi olamaz?

Arazinin alanı 12 × 12 = 144 dam2'dir. 144'ün 4'te 1'i 36 dam2'dir.

Sol alt köşesi A, B ve C noktalarına gelen ve alanı 36 dam2 olan araziler aşağıda gösterilmiştir.

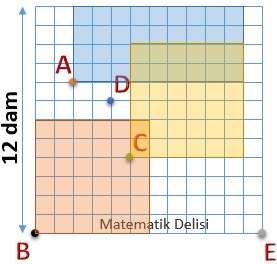
Çarpan Testi-Alan Sorusu-Çözüm

Sol alt köşenin D noktasına geldiğini düşünelim. Kare şeklindeki arazinin üst kenarı ile D noktası arasındaki uzaklık 5 dam'dır. Buna göre Ali'nin seçeceği arazinin kenar uzunluklarından biri en fazla 5 olabilir. 5, 36'nın çarpanı değildir. 36'nın 5'ten küçük en büyük çarpanı 4'tür. Buna göre arazinin diğer kenar uzunluğu en az 9 dam olmalıdır. Yalnız D noktası ile toplam arazinin sağ kenarı arasındaki uzaklık 8 dam olduğu için sol alt köşesi D olan bir arazi seçilemez.

CEVAP: D

SORU 6

Ayrıt uzunlukları a, b ve c olan bir dikdörtgenler prizmasının yüzey alanı 2(ab + bc + ac)'dir.

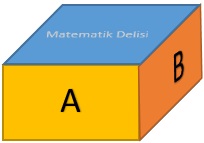
Çarpan Testi-Dikdörtgenler Prizmasının Yüzey Alanı

Ayrıt uzunlukları metre cinsinden tam sayı olan dikdörtgenler prizması şeklindeki yukarıdaki cismin A ve B yüzlerinin alanları, sırasıyla, 24 m2 ve 18 m2'dir.

Buna göre, yukarıda gösterilen dikdörtgenler prizmasının yüzey alanı en az kaç metrekaredir?

Mavi renkle gösterilen yüzün alanına C dersek dikdörtgenler prizmasının toplam yüzey alanı metrekare cinsinden

2(24 + 18 + C) = 84 + 2C

olur.

A ve B yüzlerinin ortak kenarı olan ayrıtın uzunluğu hem 24'ün hem de 18'in çarpanı olmalıdır.

  • 24'ün çarpanları: 1, 2, 3, 4, 6, 8, 12 ve 24
  • 18'in çarpanları: 1, 2, 3, 6, 9 ve 18

Ortak çarpanlar 1, 2, 3 ve 6'dır. Buna göre, ortak ayrıtın uzunluğu 1, 2, 3 veya 6 m'dir.

  • Ortak ayrıt 1 m ise, C'nin kenar uzunlukları 24 ÷ 1 = 24 m ve 18 ÷ 1 = 18 m olur. Alanı ise 24 × 18 = 432 m2 olur.
  • Ortak ayrıt 2 m ise, C'nin kenar uzunlukları 24 ÷ 2 = 12 m ve 18 ÷ 2 = 9 m olur. Alanı ise 12 × 9 = 108 m2 olur.
  • Ortak ayrıt 3 m ise, C'nin kenar uzunlukları 24 ÷ 3 = 8 m ve 18 ÷ 3 = 6 m olur. Alanı ise 8 × 6 = 48 m2 olur.
  • Ortak ayrıt 6 m ise, C'nin kenar uzunlukları 24 ÷ 6 = 4 m ve 18 ÷ 6 = 3 m olur. Alanı ise 4 × 3 = 12 m2 olur.

Yukarıda yaptığımız hesaplamalara göre C'nin alanı en az 12 m2 olabilir. Bu durumda dikdörtgenler prizmasının toplam yüzey alanı

84 + 2 × 12 = 108 m2 olur.

CEVAP: B

SORU 7

Aşağıdakilerden ifadelerden hangisi yanlıştır?

A) 1'den büyük bir tam sayının kendisi ve 1, bu sayının çarpanlarıdır. Bu nedenle, 1'den büyük bir a tam sayısının çarpanları toplamı en az a + 1 olmalıdır. Bu sayı a'dan büyüktür. → DOĞRU

B) Bir asal sayının iki çarpanı vardır: 1 ve kendisi. Bu iki sayıyının çarpımı asal sayının kendisine eşittir. → DOĞRU

C) 2, asal olmayan tek sayıların (Ör. 9, 15, 21,...) çarpanı değildir. → YANLIŞ

D) 1'den büyük bir tam sayının en az iki çarpanı vardır: kendisi ve 1. → DOĞRU

CEVAP: C

SORU 8

Bir sınıftaki öğrenciler 2'şerli, 3'erli ve 4'erli gruplara ayrıldığında geriye hiç öğrenci kalmamaktadır.

Bu sınıf hakkında aşağıdaki bilgilerden hangisi kesinlikle doğrudur?

Bu sınıftaki öğrenci sayısı 2, 3 ve 4'e tam bölünmektedir. Buna göre 2, 3 ve 4 bu sayının çarpanları içindedir.

2 ve 3 bir sayının çarpanları arasındaysa, 6 da bu sayının çarpanı olmalıdır. Diğer seçeneklerde verilen sayılar hakkında kesin yargılara varamayız.

CEVAP: B

SORU 9
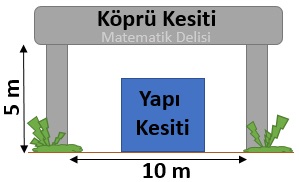
Denklem-Test-Köprü Sorusu

5 m boyundaki sütun bloklar üzerine inşa edilen bir köprünün altına dikey kesiti dikdörtgen olan bir yapı daha inşa edilecektir. Bu dikdörtgenin alanı 36 m2 ve kenar uzunlukları metre cinsinden tam sayı olacaktır. Ayrıca bu yapı, köprü veya sütun bloklarla temas etmeyecektir.

Köprüyü tutan sütun bloklar arasındaki uzaklık 10 m ise, bu yapının dikey kesitinin çevresi kaç metre olabilir?

İlk aşamada, biri 5'ten ve diğeri 10'dan küçük olan ve çarpımları 36'ya eşit olan sayıları bulmamız gerekir.

36'nın 5'ten küçük çarpanları 1, 2, 3 ve 4'tür.

4 dışındaki çarpanlar uzun kenarın 10 m'den büyük olmasına yol açar. Bu nedenle yapının kısa kenarı 4 m olmalıdır. Kısa kenarı 4 m ise uzun kenar 36 ÷ 4 = 9 m'dir. Buna göre yapının çevresi

2(4 + 9) = 2 × 13 = 26 m'dir.

CEVAP: B

SORU 10

İsmail ile Çigdem, bir çift zarla kendi aralarında matematiksel bir oyun oynamaktadırlar. Bu oyunun her bir turunda, sırası gelen kişi iki zar atmakta ve gelen sayıları birbiri ile çarparak, elde edilen sonucun 7'den küçük çarpan sayısını hesaplamaktadır. Hesaplanan çarpan sayısı, zarı atan oyuncunun hanesine puan olarak yazılmaktadır.

İsmail ilk tura 6-3 atarak başlamıştır.

Çiğdem ilk turun sonunda İsmail'i geçtiğine göre aşağıdaki sayı ikililerinden hangisini atmış olabilir?

6 × 3 = 18'dir. 18'in 7'den küçük çarpanları 1, 2, 3 ve 6'dır. Buna göre İsmail'in ilk turda aldığı puan 4'tür.

Şimdi de verilen seçeneklerden elde edilebilecek puanlara bakalım.

A) 5 × 4 = 20

20'nin 7'den küçük çarpanları 1, 2, 4 ve 5'tir. (4 puan)

B) 3 × 3 = 9

9'un 7'den küçük çarpanları 1 ve 3'tür. (2 puan)

C) 4 × 3 = 12

12'nin 7'den küçük çarpanları 1, 2, 3, 4 ve 6'dır. (5 puan)

D) 6 × 1 = 6

6'nın çarpanları 1, 2, 3 ve 6'dır. (4 puan)

Seçenekler içinde 7'den küçük çarpan sayısı 4'ten büyük olan tek sayı ikilisi 4-3'tür.

CEVAP: C

Yeniden Başlat
Yukarı Çık