Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2013-2014 2.DÖNEM SORU VE ÇÖZÜMLERİ
LİSELERE GİRİŞ SINAVI
2013-2014 TEOG 2. DÖNEM - Çıkmış Sorular ve Çözümleri
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
...... ifadesi aşağıdakilerden hangisine eşittir?
Çözüm:
Soruda 7 tane ...'un çarpımının hangi seçeneğe eşit olduğu sorulmuştur. Bu çarpım ...'un 7. kuvvetine veya ...'ye eşittir. Paydadaki üslü sayıyı paya taşırken kuvvetin işaretini değiştiririz.
...
CEVAP: A
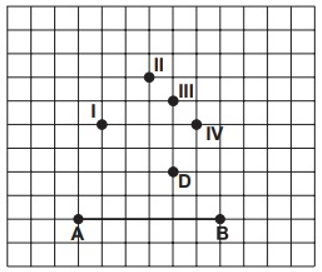
Verilen şekle göre, hangi nokta C köşesi olarak seçilirse ABC üçgeninin AB kenarına ait kenarortayı D noktasından geçer?
Çözüm:
AB kenarına ait kenarortay, bu doğru parçasının orta noktasından geçer. Hem AB'nin orta noktasından hem de D noktasından geçen bir doğru çizdiğimizde, bu doğrunun aynı zamanda IV noktasından da geçtiğini görebiliriz. Bu nedenle C noktası IV olabilir.
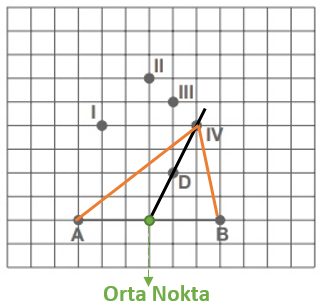
CEVAP: D
7 a 13
Yukarıda verilenler bir aritmetik dizinin ilk üç terimi olduğuna göre, a yerine hangi sayı gelmelidir?
Çözüm:
Art arda gelen terimler arasındaki fark x ise, 7 ile 13 arasındaki fark 2x'tir. 13 – 7 = 6 olduğu için x = 3'tür. Buna göre a = 7 + 3 = 10'dur.
CEVAP: C
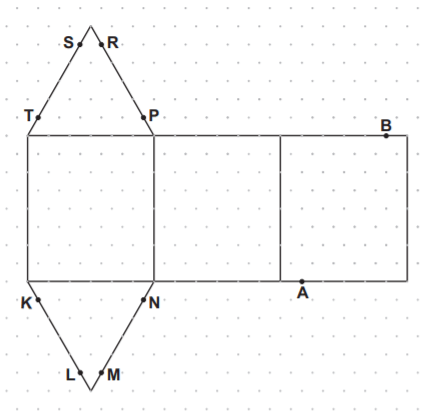
Şekilde izometrik kağıtta verilen açınım üçgen dik prizma oluşturacak şekilde kapatıldığında, A ve B noktaları hangi noktalar ile eşleşir?
Çözüm:
Verilen açınım, üçgen dik prizma oluşturacak şekilde kapatıldığında
- A noktası L ve
- B noktası T ile
üst üste gelir.
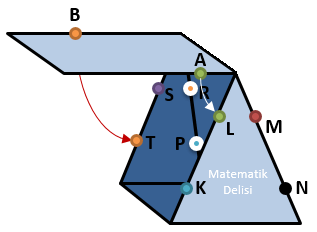
CEVAP: B
Aşağıda verilen geometrik cisimlerden hangisi, bir düzlemle kesildiğinde arakesit bir daire olamaz?
Çözüm:
A, C ve D seçeneklerindeki geometrik cisimler, bir düzlemle kesildiğinde daire şeklinde bir ara kesit elde edilebilir. Dik piramit için böyle bir ara kesit elde edilemez.
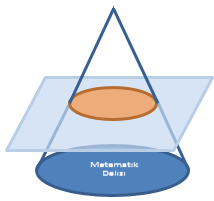
Dik dairesel koni

Dik dairesel silindir

Küre
CEVAP: B
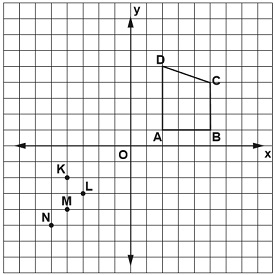
Şekildeki ABCD yamuğu orijin etrafında 180° döndürülerek A'B'C'D' yamuğu elde ediliyor.
Buna göre K, L, M, N noktalarından hangisi A'B'C'D' yamuğunun dış bölgesinde kalır?
Çözüm:
A, B, C ve D noktalarının koordinatları sırasıyla (2, 1), (5, 1), (5, 4) ve (2, 5)'tir.
Koordinatları (m, n) olan bir nokta orijin etrafında 180° döndürüldüğünde (–m, –n) koordinatlarına gelir. Buna göre A', B', C' ve D' noktaları, sırasıyla, (–2, –1), (–5, –1), (–5, –4) ve (–2, –5) koordinatlarındadır. Köşeleri A', B', C' ve D' olan yamuğu çizdiğimizde N noktasının bu yamuğun dış bölgesinde kaldığını görebiliriz.

CEVAP: D

Şekilde [DE] ⫽ [AB] dir. |CD| = 3 cm, |DE| = 4 cm ve |AB| = 12 cm olduğuna göre, |AD| kaç santimetredir?
Çözüm:

CDE ve CAB üçgenlerinin tepe açıları ortak ve taban açıları yöndeştir. Aynı iç açılara sahip olduğu için CAB ve CDE üçgenleri benzerdir.
CAB ~ CDE
Benzer olan bu üçgenlerin kenar uzunlukları arasındaki ilişki aşağıdaki gibidir.
... ...
Yukarıdaki eşitlikte değeri bilinen kenar uzunlukları yerlerine yazıldığında, |CA|'nın 9 cm'ye eşit olduğu görülebilir.
... ...
⇒ |CA| = 9 cm
|AD| uzunluğu ise, |CA| ile |CD|'nin farkına eşittir.
|AD| = |CA| – |CD| = 9 – 3 = 6 cm
CEVAP: A
Efe, bir oyun için 5 arkadaşından 3'ünü kaç farklı biçimde seçebilir?
Çözüm:
5 kişi arasından 3 kişi ... farklı şekilde seçilebilir.
CEVAP: A
Alanı 108 cm2 olan karesel bölgenin çevresinin uzunluğu kaç santimetredir?
Çözüm:
Bu karenin kenar uzunluğunu bulabilmek için alanının karekökünü alırız.
... ...
Bir kenarı ... cm olan bir karenin çevresi ... santimetredir.
CEVAP: C
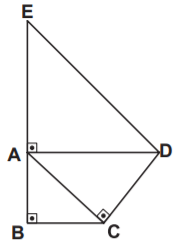
Şekildeki ..., ..., ... ikizkenar dik üçgenlerdir. |AB| = 2 cm olduğuna göre, |DE| kaç santimetredir?
Çözüm:
İkizkenar dik üçgende hipotenüsün uzunluğu, dik kenar uzunluğunun ... katıdır. |AB| = 2 cm olduğuna göre
- ... ... cm,
- ... ... cm ve
- ... ... cm'dir.
CEVAP: B
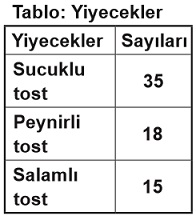
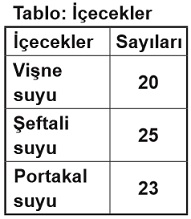
Bir okul gezisinde öğrencilere dağıtılmak üzere bir yiyecek ve bir içecekten oluşan paketler hazırlanacaktır. Tablolarda sayıları verilen yiyecek ve içeceklerden rastgele birer tane alınarak hazırlanan ilk pakette, peynirli tost ve vişne suyu olma olasılığı aşağıdaki işlemlerden hangisi ile hesaplanabilir?
Çözüm:
35 + 18 + 15 = 68 yiyecekten 18'i peynirli tosttur. Buna göre, ilk pakette peynirli tost olma olasılığı ...'dir.
20 + 25 + 23 = 68 içecek içinden 20'si vişne suyudur. İlk pakette vişne suyu olma olasılığı ...'dir.
İlk pakette hem peynirli tost hem de vişne suyu olma olasılığı ...'dir.
CEVAP: A
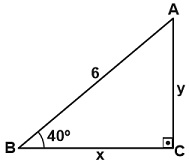
Şekildeki ABC dik üçgeninde, |AB| = 6 cm, |BC| = x cm ve |AC| = y cm olduğuna göre, aşağıda verilen eşitliklerden hangisi doğrudur?
Çözüm:
- ...,
- ...,
- ... ve
- ...'dir.
Tek doğru eşitlik C seçeneğinde verilmiştir.
CEVAP: C
Bir ABC üçgeninde ...'dir. Buna göre, üçgenin kenarları arasında aşağıdaki hangi ilişki olamaz?
Çözüm:
Bir üçgenin iç açılarından biri 100⁰ ise diğer iki açının toplamı 180⁰ – 100⁰ = 80⁰'dir. Dolayısıyla, bu üçgendeki en büyük açı 100⁰'dir.

Bir ABC üçgeninde ... açısının karşısındaki kenar BC'dir. En büyük açının karşısında en uzun kenar olduğundan bu üçgendeki en uzun kenar BC'dir. Buna göre, |BC| uzunluğu diğer kenar uzunluklarına eşit veya bu uzunluklardan küçük olamaz. D seçeneğinde, |BC| uzunluğu farklı bir kenar uzunluğuna eşitlendiğinden doğru cevap bu seçenektir.
CEVAP: D
Kenar uzunlukları santimetre cinsinden birer tam sayı ve çevresinin uzunluğu 9 cm olan kaç farklı üçgen vardır?
Çözüm:
Soruda verilen şartlara uyan kenar uzunlukları santimetre cinsinden
- 4, 4 ve 1;
- 2, 3 ve 4; veya
- 3, 3 ve 3;
olabilir.
CEVAP: A
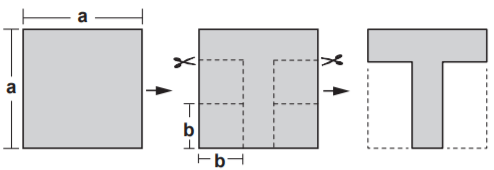
Bir kenarının uzunluğu a birim olan kare şeklindeki bir kağıttan, bir kenarının uzunluğu b birim olan kare şeklinde dört eşit parça yukarıdaki gibi kesilip çıkarılıyor. Kalan kağıdın bir yüzünün alanının kaç birimkare olduğunu gösteren cebirsel ifade aşağıdakilerden hangisi ile özdeştir?
Çözüm:
Karenin alanı bir kenar uzunluğunun karesine eşittir.
Kağıdın kesilmeden önceki alanı a2 ve kesilen her bir parçanın alanı b2'dir. Kağıttan toplam 4 parça kesildiği için kesilen toplam alan 4b2'dir. Buna göre geriye kalan kağıdın alanı a2 – 4b2'dir.
a2 – 4b2 ifadesi (a – 2b)(a + 2b) ile özdeştir.
CEVAP: D
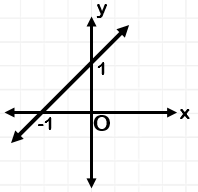
Aşağıda grafikleri verilen doğrulardan hangisinin eğimi 1'dir?



Çözüm:
... ...
Diğer seçeneklerdeki doğruların eğimleri aşağıdaki gibidir.
B) TanımsızC) –1D) 0
CEVAP: A
... cebirsel ifadesi aşağıdakilerden hangisine eşittir?
Çözüm:
3x2 – 11x + 10 ifadesinin çarpanlarına ayrılmış hali (3x – 5)(x – 2)'dir.
Paydadaki 6x – 10 ifadesini 2 parantezine alırsak, 2(3x – 5) haline dönüşür.
Pay ve paydadaki 3x – 5'leri sadeleştirdiğimizde geriye payda x – 2 ve paydada 2 kalır.
CEVAP: B
... ... denklemini sağlayan x değeri kaçtır?
Çözüm:
x'li terimleri sol tarafta ve sabit terimleri sağ tarafta toplayalım.
... ...
Sabit terimler arasındaki işlemin sonucu 3'tür. Sol taraftaki kesirlerin paydalarını eşitleyelim.
...
Kesirler arasındaki çıkarma işlemini yapalım.
...
Paydadan kurtulmak için iki tarafı da 6 ile çarpalım.
...
CEVAP: C

Birbirine özdeş olan peynir paketleri ve birbirine özdeş olan süt paketlerinin 60 cm uzunluğundaki raflara dizilişi şekilde gösterilmiştir. Birinci rafta 15 cm, ikinci rafta 10 cm boşluk kaldığına göre, üçüncü raftaki boşluk kaç santimetredir?
Çözüm:
Süt paketlerinin santimetre cinsinden uzunluğuna x ve peynir paketlerinin santimetre cinsinden uzunluğuna y dersek, birinci raftaki paketlerin toplam uzunluğu 3x + y olur. Bu rafta 15 cm boşluk kaldığına göre, paketlerin toplam uzunluğu 60 – 15 = 45 cm'dir. Buna göre 3x + y = 45'tir. Benzer şekilde, ikinci raftaki paketlerin toplam uzunluğu x + 2y'dir. Rafta bu paketlerin kapladığı bölge 60 – 10 = 50 cm'dir. Buna göre, x + 2y = 50'dir.
Bulduğumuz denklemler aşağıdaki denklem sistemini oluşturur.
3x + y = 45
x + 2y = 50
İkinci denklemi –3 ile çarpıp, ilk denklemle toplarsak, y'nin 21 cm olduğunu görebiliriz.
3x + y – 3x – 6y = 45 – 150
⇒ –5y = –105
⇒ y = 21
Yukarıda bulduğumuz sonuca göre üçüncü raftaki boşluk 60 – 21 = 39 cm'dir.
CEVAP: D
Koordinat sisteminde denklemleri, y = 4 ve y = x olan doğrular ile y ekseninin sınırladığı bölgenin alanı kaç birimkaredir?
Çözüm:
Aşağıdaki şekilde
- y = 4 doğrusu
turuncu ve - y = x doğrusu
yeşil renkte
gösterilmiştir. Bu doğrular ile y-ekseni arasında kalan bölge ise
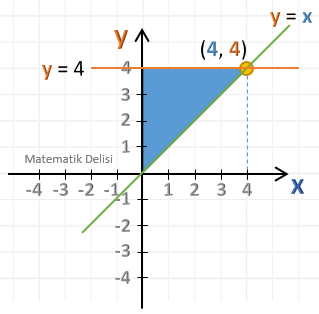
Soruda alanı istenilen bölge dik üçgen şeklindedir. Tabanı ve yüksekliği 4 birim olan bu dik üçgenin alanı, ... birimkaredir.
CEVAP: B
Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2013-2014 2.DÖNEM SORU VE ÇÖZÜMLERİ