Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2014-2015 2.DÖNEM MAZERET-SORU VE ÇÖZÜMLERİ
LİSELERE GİRİŞ SINAVI
2014-2015 TEOG 2. DÖNEM MAZERET SINAVI - Çıkmış Sorular ve Çözümleri
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
75 . 75 işleminin sonucu aşağıdakilerden hangisine eşittir?
Çözüm:
Tabanları aynı olan üslü ifadeleri çarparken kuvvetleri toplarız.
75 . 75 = 75 + 5 = 710
CEVAP: B
Aşağıdaki cisimlerden hangisi tabanına dik bir düzlemle kesildiğinde ara kesit bir üçgen olamaz?


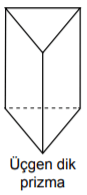

Çözüm:
Dik koni, üçgen dik piramit ve kare dik piramitin tabana dik ara kesitleri üçgen olabilir. Üçgen dik prizma için aynı durum söz konusu değildir.
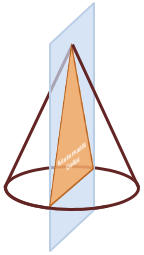
Dik Koni
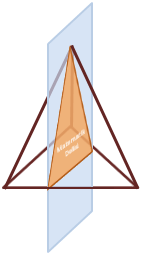
Üçgen Dik Piramit
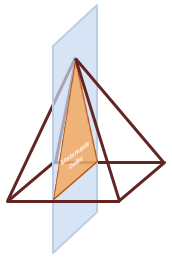
Kare Dik Piramit
CEVAP: C
..., ..., ..., ..., ..., ...
Yukarıdaki geometrik dizide ... kaçtır?
Çözüm:
Bu geometrik dizide 2. terimi 1. terime böldüğümüzde, her bir terimin bir öncekinin ... katı olduğunu görebiliriz.
...
Buna göre
- ... ve
- ...'dir.
Bulduğumuz değerleri kullanarak ... ile ...'nin çarpımının 4 . 8 = 32 olduğunu görebiliriz.
CEVAP: D
Aşağıda verilenlerden hangisi yanlıştır?
Çözüm:

Gerçek sayılar kümesi ile irrasyonel sayılar kümesinin kesişimi irrasyonel sayılar kümesidir. A seçeneğinde verilen bilgi yanlıştır.
CEVAP: A
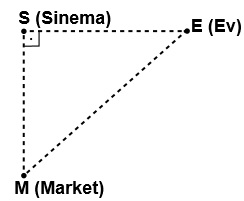
Yukarıdaki modelde ev, sinema ve marketin konumları bir dik üçgenin köşeleri olup E, S ve M harfleri ile gösterilmektedir.
Buna göre, evin sinemaya uzaklığının evin markete uzaklığına oranı, aşağıdakilerden hangisine eşittir?
Çözüm:
Evin sinemaya uzaklığının evin markete uzaklığına oranı ... açısının kosinüsüne eşittir.
CEVAP: D

Şekildeki ... dik üçgeninde ... ve ...'dir. [AD], ...’nın açıortayı olduğuna göre aşağıdaki doğru parçalarından hangisi en uzundur?
Çözüm:
Bu soruyu çözebilmek için önce şekildeki tüm iç açıları bulmamız gerekiyor. Kenar uzunlukları arasındaki sıralamaları bulabilmek için bu iç açıları kullanıyoruz.
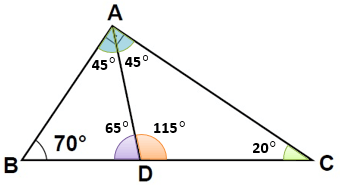
İç Açılar:
... üçgeninin iç açılarından ikisi 70⁰ ve 90⁰'dir. Üçüncü iç açıyı bulabilmek için bu açıların toplamını 180⁰'den çıkarabiliriz.
... ... ...
[AD] açıortay olduğuna göre, hem ... hem de ..., 90⁰'nin yarısına eşittir.
...
... açısının değerini bulabilmek için ... üçgeninde değerini bildiğimiz açıların toplamını 180⁰'den çıkarabiliriz.
... ... ...
... üçgenin iç açılarından ikisinin 45⁰ ve 20⁰ olduğunu gördük. Geriye kalan son kalan açıyı hesaplayabilmek için bu üçgenin iç açıları toplamını 180⁰'ye eşitleyebiliriz.
... ... ...

Şimdi bulduğumuz iç açıları kullanarak, kenar uzunlukları arasındaki büyüklük-küçüklük ilişkilerini elde edelim.
Kenar Uzunlukları:
-
... üçgenindeki en büyük açı ... olduğundan [AB], [BD] ve [AD] doğru parçaları arasındaki en uzun kenar bu açının karşısındaki [AD]’dir.
|AD| > |AB| > |BD|
-
... üçgenindeki en büyük açı ... olduğundan bu üçgendeki en uzun kenar [AC]’dir. Böylece [AD], [DC] ve [AC] doğru parçaları arasından en uzununun [AC] olduğunu görebiliriz. Bu nedenle, cevap B’dir.
|AC| > |DC| > |AD|
CEVAP: B
Bir çeşitkenar üçgenin kenarlarından ikisinin uzunlukları 6 cm ve 7 cm’dir.
Bu üçgenin üçüncü kenarının uzunluğunun santimetre cinsinden alabileceği kaç tam sayı değeri vardır?
Çözüm:
Üçgenin bir kenar uzunluğu, diğer iki kenar uzunluğunun toplamı ile farkı arasındadır. Kenarlardan ikisi 6 cm ve 7 cm uzunluğunda olduğuna göre üçüncü kenarın uzunluğu 6 + 7 = 13 cm'den küçük ve 7 – 6 = 1 cm'den büyüktür. 13'ten küçük ve 1'den büyük tam sayılar
2, 3, 4, 5,
Yalnız, üçgenin çeşitkenar olduğu için bu listeden
CEVAP: C

Şekilde [DE] ⫽ [BC] ve [EC] ⫽ [AB]'dir. |AB| = 12 cm, |AD| = 6 cm ve |EC| = 4 cm olduğuna göre, |DC| kaç santimetredir?
Çözüm:
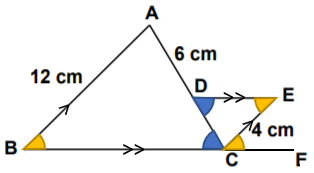
[BC] doğru parçasını sağa doğru uzatalım.
[EC] ⫽ [AB] olduğu için ... ve ... açıları yöndeştir. Ayrıca, [DE] ⫽ [BC] olduğu için ... ile ... iç ters açılardır. Buna göre,
...'dir.
... ve ... açıları iç ters açılardır ve ölçüleri eşittir.
İç açıları aynı olduğu için ABC ve CED üçgenleri benzerdir. CED üçgeninin ABC üçgenine benzerlik oranı
...'tür.
Bu benzerlik oranı, diğer bir eş açının karşısında olan [DC] ve [AC] kenarları arasında da bulunmalıdır. |DC| uzunluğuna x dersek, |AC| uzunluğu 6 + x olur. Bu iki uzunluğu oranlayıp, benzerlik oranına eşitlediğimizde |DC|'nin 3 cm'ye eşit olduğunu görebiliriz.
...
⇒ ...
⇒ ...
⇒ ...
CEVAP: D
Her birinin alanı 18 cm2 olan iki eş dikdörtgenin uzun kenarları çakıştırıldığında bir kare oluşuyor.
Bu karenin bir kenarının uzunluğu kaç santimetredir?
Çözüm:
Her birinin alanı 18 cm2 olan iki dikdörtgenin toplam alanı 18 + 18 = 36 cm2'dir. 36 cm2'lik alana sahip bir karenin kenar uzunluğu ise ... cm'dir.
CEVAP: A
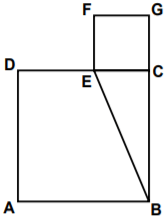
Şekildeki ABCD ve FECG karedir. A(ABCD) = 144 cm2 ve A(FECG) = 25 cm2 olduğuna göre, |EB| kaç santimetredir?
Çözüm:
ECB üçgeninin dik kenar uzunluklarını bulalım.
- A(ABCD) = 144 cm2 olduğundan |BC| = ... cm ve
- A(FECG) = 25 cm2 olduğundan |EC| = ... cm’dir.
EB doğru parçası, ECB üçgeninin hipotenüsüdür. |EB| uzunluğunu uzunluğunu bulabilmek için Pisagor bağıntısını kullanabiliriz.
|EB| = ... ... ... ... cm
CEVAP: B
K, U, V, V, E, T harflerinin tamamı her yüzde bir harf olacak şekilde bir küpün yüzlerine yazılıyor.
Bu küp iki kez atıldığında üst yüzüne sırasıyla E, V harflerinin gelme olasılığı nedir?
Çözüm:
KUVVET sözcüğündeki 6 harften 2'si V ve 1'i E'dir. Buna göre küp atıldığında E harfinin gelme olasılığı ... ve V harfinin gelme olasılığı ...'dır. Bu iki olay birbirinden bağımsız olduğu için istenen olasılık ...'dir.
CEVAP: A

Şekildeki A, B, C noktaları m doğrusu üzerinde ve D, E noktaları n doğrusunun üzerindedir.
Buna göre, köşeleri bu noktalardan herhangi üçü olan kaç farklı üçgen çizilebilir?
Çözüm:
Çizilecek üçgenlerin bir kısmının 2 köşesi m ve diğerlerinin 2 köşesi n üzerinde olmalıdır.
2 köşesi m üzerinde olan üçgenler:
m doğrusu üzerinde 3 noktadan 2'si ... farklı şekilde seçilebilir. n doğrusu üzerindeki 2 noktadan 1'i 2 farklı şekilde seçilebilir. Buna göre, 2 köşesi m üzerinde olan 3. 2 = 6 üçgen çizilebilir.
2 köşesi n üzerinde olan üçgenler:
m doğrusu üzerindeki 3 noktadan 1'i, 3 farklı şekilde seçilebilir. Bu nedenle 2 köşesi n üzerinde olan 3 farklı üçgen çizilebilir.
Toplamda 6 + 3 = 9 üçgen çizilebilir.
CEVAP: B

Şekilde [AE] ve [BD], C noktasında kesişmektedir. ... eşliği bilindiğine göre, aşağıdakilerden hangisi her zaman doğrudur?
Çözüm:
ABC ve EDC üçgenlerinin eş olması, A ve E noktalarındaki açıların eşit olduğu gösterir. Bu açıların eşit olabilmesi için [AB] ve [DE]'nin paralel olması gerekir.
CEVAP: C

Yukarıdaki tablo bir bilgisayar mağazasaının altı günde yaptığı günlük bilgisayar satış sayılarını göstermektedir.
Tablodaki veri grubunun standart sapması kaçtır?
Çözüm:
Bilgisayar satışlarının aritmetik ortalaması 6'dır.
...
Satış rakamları ile aritmetik ortalama arasındaki farkların kareleri toplamı 20'dir.
(6 – 6)2 + (6 – 5)2 + (6 – 3)2 + (6 – 7)2 + (6 – 6)2 + (6 – 9)2 = 20
Buna göre bilgisayar satışlarının standart sapması 2'ye eşittir.
... ...
CEVAP: A
Alanı a2 metrekare olan arsaya alanı b2 metrekare olan bir ev yapılıyor.
a ve b'nin alabileceği her değer için arsanın kalan kısmının alanını gösteren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
Soruda verilenlere göre arsanın alanı a2 ve evin alanı b2'dir.
Arsanın alanından evin alanını çıkarırsak geriye kalan alanı bulabiliriz. İstenilen alan a2 – b2'dir.
a2 – b2 = (a + b)(a – b)
olduğunu için cevap C'dir.
CEVAP: C
... cebirsel ifadesi aşağıdakilerden hangisine eşittir?
Çözüm:
x2 + 5x + 4 yerine (x + 1)(x + 4) yazdığımızda, pay ve paydadaki x + 1'ler sadeleşir ve geriye x + 4 kalır.
CEVAP: D

Verilen koordinat sisteminde A(3, 0) ve B(0, 6) noktalarından geçen d doğrusunun eğimi nedir?
Çözüm:
A ve B noktalarının koordinatlarını fomülde yerine yazdığımızda eğimin
... ...
CEVAP: B
Bir sayının 3 fazlasının yarısı, aynı sayının 2 eksiğinin ...’ine eşittir.
Bu sayının 1 fazlasının yarısı kaçtır?
Çözüm:
Bu sayıya ... dersek, ilk cümledeki ifadeyi matematiksel olarak,
... ...
ile gösterebiliriz.
Soldaki ifadenin paydasını karşı tarafa çarpım olarak geçirelim.
... ...
Benzer şekilde, eşitliğin sağındaki ifadenin paydasını sol tarafa çarpım olarak geçirelim.
... ...
Parantezleri açalım.
... ...
Sağdaki ...'i sol tarafa ve soldaki 9'u sağ tarafa geçirelim.
... ...
Soldaki işlemin sonucu ...'e ve sağdaki işlemin sonucu –13'e eşittir. Bu nedenle aradığımız sayı ...'tür.
–13'ün 1 fazlası –12'ye ve –12 'nin yarısı –6'ya eşittir.
CEVAP: A
Denklemleri x = 2 ve y = –x + 3 olan doğrularla x ve y eksenlerinin sınırladığı yamuğun alanı kaç birimkaredir?
Çözüm:
Bu soruyu çözebilmek için öncelikle koordinat sisteminde x = 2 ve y = –x + 3 denklemlerinin grafiklerini çizmemiz gerekir.
x = 2'nin grafiği (2, 0) noktasından geçen ve x eksenine dik bir doğrudur.
y = –x + 3 denkleminde x yerine 0 koyduğumuzda y = 3 çıkar. Aynı denklemde y yerine 0 koyduğumuzda ise x = 3 çıkar. Buna göre, ikinci denklemin grafiği (0, 3) ve (3, 0) noktalarından geçen bir doğrudur. Bu doğruların ve x ve y eksenleri arasında kalan yamuk aşağıdaki grafikte verilmiştir.

Yamuğun tabanları 1 ve 3, yüksekliği ise 2 birim olduğundan, alanı
... birimkaredir.
CEVAP: B
Aşağıdakilerden hangisi bir kare dik prizmanın açınımı olamaz?
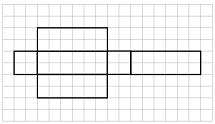

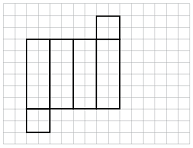

Çözüm:
D seçeneğindeki dikdörtgenleri katladığımızda alt ve üst yüzeyleri oluşturması gereken karelerin üst üste geldiğini görebiliriz. Bu seçenekteki açınım bir kare dik prizma oluşturmaz.
CEVAP: D
Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ TEOG 2014-2015 2.DÖNEM MAZERET-SORU VE ÇÖZÜMLERİ