SÜRE
30:002017-2018 LGS MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2017-2018 LGS
SÜRE
30:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
Kenarlarının uzunlukları 6 cm ve 8 cm olan bir dikdörtgene benzer olacak şekilde, kenar uzunlukları santimetre cinsinden doğal sayı olan bir dikdörtgen çizilecektir.
Çizilecek bu dikdörtgenin alanı 48 santimetreden büyük olacağına göre en az kaç santimetrekaredir?
Benzer dikdörtgenlerde kenar uzunluklarının oranı sabittir. Verilen ölçülere göre bu oran ...'dir. Bu kesrin en sade hali
...'tür.
Çizilecek dikdörtgenin kenar uzunlukları birer doğal sayı olacağına göre, kısa ve uzun kenarlar sırasıyla 3 ve 4'ün tam katı olmalıdır. x bir doğal sayı olmak üzere, kısa kenara 3x ve uzun kenara 4x dersek, bu dikdörtgenin alanı
3x . 4x = 12x2
olur. x yerine yazacağımız farklı doğal sayılar bize farklı alanlar verir. Örneğin, x=1 için alan 12; x = 2 için alan 48; ve x = 3 için alan 108 olur.
48 santimetreden büyük en küçük alan sorulduğuna göre doğru cevap 108'dir.
CEVAP: B

Yukarıdaki sayı doğrusunda 7 ile 10'a karşılık gelen noktaların arası 6 eş parçaya ayrılmıştır.
Buna göre A noktasına karşılık gelen sayı aşağıdakilerden hangisi olabilir?
7 ile 10 arası 6 eşit parçaya ayrılırsa, her bir aralık yarım birime denk gelir. Bu nedenle A noktası 8 ile 8,5 arasındadır. Başka bir ifadeyle 8 ile 9 arasında ve 8'e daha yakındır.
8 ile 9 arasındaki kareköklü bir ifadede, karekök içerisindeki sayı 82 = 64 ile 92 = 81 arasında olması gerekir. Bu şarta sadece C ve D seçeneğinde verilen ifadeler uymaktadır.
Bu sayının 8'e daha yakın olabilmesi için kök içerisindeki sayının 64'e daha yakın olması gerekir. 79 sayısı 81'e ve 68 sayısı 64'e daha yakındır. Bu nedenle cevap D'dir.
CEVAP: D
Ahmet her gün kumbarasından aynı miktarda para alarak harcıyor. Ahmet’in kumbarasındaki para miktarı ve harcadığı toplam para miktarını gösteren doğrusal grafik aşağıda verilmiştir.
Grafik: Kumbarada Bulunan ve Harcanan Toplam Para Miktarı

Grafiğe göre Ahmet’in kumbarasındaki para kaçıncı günde biter?
Ahmet'in harcadığı para ile kumbarasında kalan paraların toplamı sabittir. Bu iki miktar 10. günde eşitlendiğine göre, Ahmet 10 günde kumbaradaki paranın yarısını harcamıştır. Buna göre, parasının tamamını 20 günde harcar.
CEVAP: A
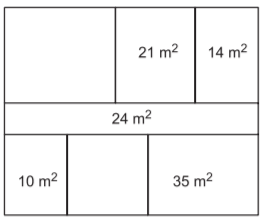
Yukarıdaki her bir bölümü dikdörtgen şeklinde olan dikdörtgen biçimindeki kat planı üzerinde bazı bölümlerin alanları verilmiştir.
Bu dikdörtgenlerin her birinin kenar uzunlukları metre cinsinden birer doğal sayı olduğuna göre alanı verilmeyen bölümlerin alanları toplamı en az kaç metrekaredir?
Toplam alanlarını hesaplayacağımız bölümleri
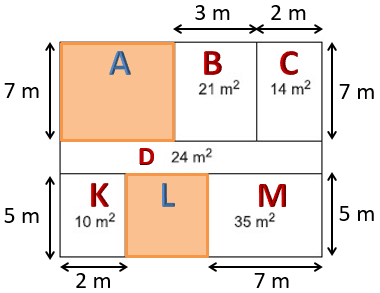
Soruda verilenlere göre, tüm bölgeler dikdörtgen şeklindedir ve kenar uzunlukları doğal sayıdır. Dikdörtgenin alanı kenar uzunluklarının çarpımına eşit olduğu için kat planındaki bir bölümün kenar uzunlukları, alanının çarpanlarıdır.
Kat planının geometrisinden dolayı,
Buna göre
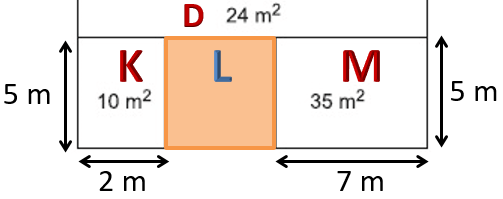
Verilen alanları kullanarak
(Bir sonraki adımda,
A bölümü:
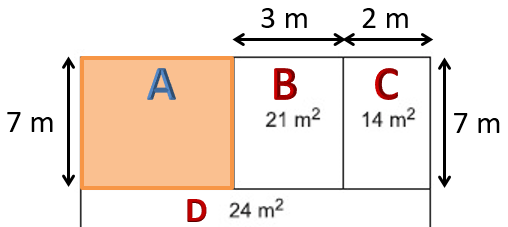
Ortak çarpanlar 1 ve 7'dir.
Verilen alanları ve bulduğumuz yüksekliği kullanarak
Toplam Alan
Yukarıdaki çıkarımlara göre,
CEVAP: C
21 000 m2 lik bir arsa ortaklar arasında paylaştırılacaktır. Paylaşım için arsanın tamamı 250 m2, 500 m2 ve 1000 m2 lik bölümlere ayrılıyor. Toplam bölüm sayısı ortakların sayısına eşittir. Her bir bölüm numaralandırılıyor ve numaralar özdeş kartların üzerine yazılarak boş bir torbaya atılıyor. Arsanın ortakları arasında çekilecek kura ile bu bölümlerin sahipleri belirlenecektir.
Bu kurada torbadan çekilecek ilk kartın üzerinde yazan numaranın; alanı 250 m2, 500 m2 ve 1000 m2 olan bölümlerden birine ait olma olasılıkları eşit olduğuna göre bu arsanın kaç ortağı vardır?
İlk çekilen numaranın, alanı 250 m2, 500 m2 ve 1000 m2 olan bölümlerden birine ait olma olasılıkları eşitse, bu bölümlerin sayıları eşittir. Alanı aynı olan bölümlerin sayısına x dersek
Buna göre, x cinsinden toplam alan 250x + 500x + 1000x = 1750x'tir. Bu sayı 21 000'e eşit olduğuna göre her çeşit karttan 21 000 ÷ 1750 = 12 tane bulunmaktadır. Dolayısıyla toplam kart sayısı 3 × 12 = 36'dır. Ortak sayısı bölüm sayısına eşit olduğuna göre bu arsanın 36 ortağı vardır.
CEVAP: B
Altan ve Can, defterlerine kenar uzunlukları santimetre cinsinden doğal sayı olan birer kare çiziyorlar. Altan'ın çizdiği karenin alanı kenar uzunlukları 7 cm ve 9 cm olan bir dikdörtgenin alanından büyük, Can'ın çizdiği karenin alanı ise bu dikdörtgenin alanından küçüktür.
Buna göre Altan ve Can'ın çizdiği karelerin alanları arasındaki fark en az kaç santimetrekaredir?
Altan ve Can'ın çizdiği karelerin kenar uzunlukları doğal sayı olduğu için alanları tam karedir.
Soruda verilen dikdörtgenin alanı 7 × 9 = 63 cm2'dir. Bu bilgilere göre,
Altan'ın çizdiği karenin alanı en az 64 cm2'dir. Can'ın çizdiği karenin alanı ise en fazla 49 cm2'dir. Buna göre, karelerin alanları arasındaki fark en az 64 – 49 = 15 cm2 olabilir.
CEVAP: B
Etkileşimli çalışmalar oluşturulabilecek bir programlama dilinde istenen hareketler tanımlı blokların uygun şekilde yerleştirilmesiyle elde edilmektedir. Bu programlama dilinde bulunan bazı bloklar ve tanımları aşağıda verilmiştir.

Örnek:



Kareli kağıtta verilen 1. şekildeki (–3, –1) noktasına yukarıdaki bloklarla belirtilen hareketler yukarıdan aşağı doğru uygulandığında 2. şekildeki (2, 5) noktası elde edilmiştir.
Buna göre K(–1, 5) noktasına aşağıdaki hareketlerden hangisi uygulanırsa L(–4, –1) noktası elde edilir?
Soruda anlatılan hareket, öteleme hareketidir. Özetle, (–1, 5) noktasına hangi öteleme hareketleri uygulandığında (–4, –1) noktasına ulaşılacağı sorulmaktadır.
Dolayısıyla, bu soruda hangi seçenekteki hareketlerin 6 birim aşağı ve 3 birim sola ötelemeye karşılık geldiği sorulmaktadır. 180 yönü aşağı tarafı ve –90 yönü sol tarafı göstermektedir. Buna göre istenen hareketleri gerçekleştiren bloklar aşağıdaki gibidir.
Bu hareketler, C seçeneğinde verilmiştir.
CEVAP: C
Bir kenarının uzunluğu 10 m olan kare şeklindeki bir bahçenin sadece köşelerinde birer sulama sistemi vardır. Her bir sulama sistemi, bulunduğu köşeye uzaklığı en fazla 4 m olan kısma kadar sulama yapabilmektedir. Bu bahçenin sulama yapılamayan kısmında tabanı kare şeklindeolan bir çardak bulunmaktadır. Bu çardağın tabanının köşegeni ile bahçenin köşegeni çakışıktır.
Taban köşegeninin uzunluğu metre cinsinden bir doğal sayı olan bu çardağın taban alanı en fazla kaç metrekaredir?

Soruda anlatılan bahçenin üstten görünüşü yukarıda verilmiştir. Bu grafikteki mavi bölgeler sulama yapılabilen alanları göstermektedir.

Çardağın sulama yapılmayan bir alanda olabilmesi için mavi alanlarla kesişmemesi gerekir. Ayrıca, soruda verilenlere göre çardağın köşegeni ile bahçenin köşegeni çakışmaktadır. Bu bilgiler ışığında, çardağın konumunun yukarıdaki mor renkli kareyle gösterildiğini düşünebiliriz.
Kenar uzunluğu 10 m olan bir karenin köşegen uzunluğu ... metredir.Mavi kısımlardan her birinin yarıçapı 4 m olduğu için köşegen üzerindeki 2 × 4 = 8 m'yi sulama alanları kaplamaktadır. Çardağın köşegeni, geriye kalan ... metrelik kısım üzerinde olmalıdır. Çardağın köşegen uzunluğu bir doğal sayı olduğu için bu uzunluk...'den küçük en büyük doğal sayıya eşittir.
200 sayısı 142 = 196 ile 152 = 225 arasındadır. Bu nedenle ... ifadesi 14 ile 15 arasındadır. Buradan ...'in 6 ile 7 arasında olduğunu çıkarabiliriz.
6 ile 7 arasındaki bir sayıdan küçük en büyük doğal sayı 6'dır. Bu nedenle çardağın köşegeni en fazla 6 m olabilir.
Köşegen uzunluğu ... olan bir karenin alanı ...'ye eşit olduğu için bu çardağın alanı en fazla ... m2 olabilir.
CEVAP: A
0,00013 × 10a ifadesinin değeri 1000'den büyüktür.
Buna göre a'nın alabileceği en küçük tam sayı değeri kaçtır?
a'nın değerine göre, çarpma işleminin sonucunda 13, 130, 1300, 13 000 gibi sayılardan biri elde edilir. Bu sayılardan 1000'den büyük olanların en küçüğü 1300'dür. Buna göre, a'nın hangi tam sayı değeri için 0,00013 × 10a'nın 1300'e eşit olduğunu bulmamız gerekir.
1300 sayısı 1300 × 100'a eşittir. Bu gösteriminde katsayının 0,00013 olabilmesi için virgülü 7 basamak sola kaydırmamız gerekir. Virgülü 7 basamak sola kaydırmak 10'un kuvvetini 0'dan 7'ye çıkarır.
0,00013 × 107 = 1300
CEVAP: B
Aşağıdaki tabloda bir lokantada satılan ve her gramında eşit kalori bulunan yemeklerin kütle ve kalorileri verilmiştir.
Tablo: Yemeklerin 100 Gramındaki Kalori Miktarları
| Yemek | Kalori |
| Çorba | 45 |
| Pilav | 72 |
| Nohut | 40 |
Lokantadaki yemekler her bir tabakta 100 gram yemek olacak şekilde satılmaktadır.
Bu lokantadan toplam 538 kalori değerinde 10 tabak yemek sipariş verildiğinde kaç tabak nohut sipariş vermiş olunur?
Toplam kalori değerinin birler basamağında 8 rakamını görüyoruz. Bu rakamı kullanarak kaç tabak pilav sipariş edildiğini bulabiliriz.

Pilavların toplam kalori değerinin birler basamağındaki rakam 8'se, sipariş edilen tabak sayısı ya 4 ya da 9'dur. 9 tabak pilav 9 × 72 = 648 kalori yapar. Bu değer soruda verilen toplam kaloriden fazla olduğu için sipariş edilen pilav sayısı 4'tür. Pilavlardan elde edilen toplam kalori değeri ise 4 × 72 = 288'dir.
Geriye kalan 538 – 288 = 250 kalori, 10 – 4 = 6 tabak çorba ve nohuttan elde edilmiştir. Sipariş edilen nohut x tabaksa, çorba 6 – x tabaktır. Buna göre, nohutlardan elde edilen kalori miktarı 40x ve çorbalardan elde edilen kalori miktarı 45(6 – x)'tir. Bu iki sayının toplamı 250'ye eşittir.
40x + 45(6 – x) = 250
⇒ 40x + 270 – 45x = 250
⇒ 270 – 250 = 45x – 40x
⇒ 20 = 5x
⇒ x = 4
CEVAP: C

Küp şeklindeki kutunun tüm yüzlerine şekildeki gibi eşit büyüklükte şeritler yapıştırılıyor ve şeritler dışında kalan üçgen biçimindeki bölgeler boyanıyor.
Buna göre, boyanan bölgenin alanını birimkare cinsinden gösteren cebirsel ifade aşağıdakilerden hangisidir?
Bir küpün 6 yüzü vardır. Küpün tüm yüzeyindeki boyalı bölgenin alanını hesaplayabilmek için yüzlerden yalnız birindeki boyalı bölgeyi x ve y cinsinden bulup, bulduğumuz ifadeyi 6 ile çarpabiliriz.
Bir yüzdeki boyalı bölge, 2 üçgenden oluşmaktadır. Bu üçgenlerin ikisi de ikizkenar dik üçgendir.

Büyük üçgenin dik kenarları y birim ve küçük üçgenin dik kenarları y – x birimdir.
Büyük üçgenin alanı:
...
Küçük üçgenin alanı:
......
Bu iki alanın toplamı:
......
6 yüzün toplam alanı:
......
CEVAP: A
Kareli kağıtta verilen aşağıdaki dikdörtgenlerden üçü aynı üçgen prizmaya ait yüzlerdir
Buna göre hangisi bu üçgen prizmanın bir yüzü olamaz?
Üçgen prizmanın alt ve üst yüzleri üçgen, yan yüzleri ise dikdörtgen şeklindedir. Seçeneklerdeki dikdörtgenler, üçgen prizmanın yan yüzlerini oluşturacaktır. Bu dikdörtgenlerin kenar uzunlukları,
Seçeneklerdeki dikdörtgenlerden hangi üçü seçilirse seçilsin, 6 birimlik kenar uzunluğu ortaktır. Buna göre, prizmanın yüksekliği 6 birim olmalıdır. Dikdörtgenlerin diğer kenar uzunlukları tabandaki üçgeni oluşturacaktır. Bu kenar uzunlukları sırasıyla, 5, 3, 11 ve 6 birimdir. Yalnız uzun kenarı 11 birim olan dikdörtgen seçildiğinde, geriye kalan uzunlukların ikili toplamları 11'den yüksek olmadığı için tabanda bir üçgen oluşmaz. Bu nedenle, C seçeneğindeki uzun kenarı 11 birim olan dikdörtgen bu prizmanın yan yüzlerinden biri olamaz.
CEVAP: C
Aşağıdakilerden hangisi
3x2 – 6xy + 3y2
cebirsel ifadesinin çarpanlarından biridir?
Katsayıların tümü 3'ün tam katı olduğu için bu ifadeyi 3 parantezine alalım.
3x2 – 6xy + 3y2 = 3(x2 – 2xy + y2)
Parantez içerisindeki ifade (x – y)2'ye eşittir. Aynı zamanda bu ifade (y – x)2'ye de eşittir. Bu nedenle çarpanlarından biri y – x'tir.
CEVAP: B

Beyaz kartondan yapılmış bir kare dik piramidin dış yüzünün bir kısmı griye boyanıyor. Bu kare dik piramidin açınımı yapıldığında dış yüzü yukarıdaki gibi görünüyor.
Buna göre aşağıdakilerden hangisi bu piramidin görünümlerinden biri olamaz?
Piramidi oluşturan üçgen şeklindeki yan yüzlere numaralar verelim.

Piramidi kapattığımızda, taban alta gelecek şekilde, soldan sağa doğru yan yüzleri takip ettiğimizde 1⇒2⇒3⇒4⇒1 sıralamasını görmemiz gerekir.
Verilen seçenekler için soldan sağa doğru yan yüzlerin numaralarını yazalım.
D seçeneğindeki sıralama 1⇒2⇒3⇒4⇒1 dizisine uymamaktadır. Bu seçenekte verilen görünüm, sorudaki piramide ait olamaz.
CEVAP: D
İki farklı yüzme kursuna ait ücretler aşağıdaki tabloda verilmiştir.
Tablo: Kursların Ücretleri
| Kurslar | Kayıt Ücreti (TL) | Aylık Ücret (TL) |
| 1. Kurs | 310 | 40 |
| 2. Kurs | 130 | 55 |
Yüzme kursuna katılan bir kişi bir defalık kayıt ücreti ve devam ettiği her ay için aylık ücret ödemektedir.
Tabloda ücretleri verilen kurslardan birine katılmak isteyen bir kişinin en az kaç ay kursa devam etmesi durumunda 1. kursa katılması daha ekonomik olur?
Bu kişinin kurslardan birine toplam x ay devam ettiğini düşünelim.
1. kursun daha ekonomik olabilmesi için aşağıdaki eşitsizliğin sağlaması gerekir.
310 + 40x < 130 + 55x
Eşitsizliğin Çözümü:
Sabit terimleri solda ve x'li terimleri sağda toplayalım.
310 – 130 < 55x – 40x
Sol ve sağ taraftaki işlemleri yapalım.
180 < 15x
İki tarafı da 15'e bölelim.
12 < x
Buna göre, x'in alabileceği en küçük tam sayı değeri 13'tür.
CEVAP: C
Bir telefon şirketi müşterilerine fatura ödemelerinde iki indirim seçeneği sunmaktadır.
1. seçenek: Fatura tutarında % 10 indirim
2. seçenek: Fatura tutarında 4 lira indirim
1. seçeneği tercih eden bir müşteri 2. seçeneği tercih etmiş olsaydı 3 lira daha fazla ödeme yapacaktı.
Buna göre bu müşterinin fatura tutarı kaç liradır?
Bir fiyatta % 10 indirim yapılması, bu fiyatın % 90'ına düşeceği anlamına gelir. % 90'ın kesirli gösterimi ...'dur.
Fatura tutarına x dersek,
2. seçenek, 1. seçenekten 3 lira fazlaysa, 1. seçeneğe 3 lira eklediğimizde ödemeler eşitlenir. Matematiksel olarak bunu
... ...
şeklinde ifade edebiliriz. Oluşturduğumuz denklemi çözebilmek için x'li terimleri sol tarafta ve sabit terimleri sağ tarafta toplayalım.
...
Sol ve sağ taraftaki terimler arasındaki işlemleri yapalım.
...
İki tarafı da 10'la çarparsak, fatura tutarının 70 lira olduğunu görebiliriz.
CEVAP: D
Alanı 118 m2 olan bir evin dikdörtgen biçimindeki odaları ve salonu dışındaki bölümlerinin toplam alanı 34 m2 dir. Salonun alanı, metrekare cinsinden bir tamkare sayıdır ve odaların alanları toplamından küçüktür.
Bu salonun kısa kenarının uzunluğu ... m olduğuna göre uzun kenarının uzunluğu en fazla kaç metredir?
Odaların ve salonun toplam alanı 118 – 34 = 84 m2'dir.
Salonun alanı, odaların alanından küçük olduğuna göre, toplam alanın yarısından daha küçük olmalıdır.
Salonun alanı < 42 m2
Soruda bu alanın tam kare olduğu da verilmiştir. Buna göre, salonun alanı 42'den küçük bir tam karedir.
Kenar uzunlukluğunun olası en yüksek değerini bulabilmek için alanın en yüksek değerini kullanmamız gerekir. 42'den küçük tam kare sayıların en büyüğü 36'dır. Buna göre soruda istenilen kenar uzunluğu en fazla
......... m
olabilir.
CEVAP: B

ABC üçgeninde ... > ..., |AB| = 8 cm ve |BC| = 10 cm'dir.
Buna göre |AC|'nun santimetre cinsinden alabileceği kaç farklı tam sayı değeri vardır?
Bu üçgende A açısının B açısından büyük olması |AC| uzunluğunun 10 cm'den küçük olduğu anlamına gelir. 10'dan küçük pozitif tam sayılar 1, 2, 3, 4, 5, 6, 7, 8 ve 9'dur.
|BC| ve |AB| arasındaki fark |BC| – |AB| = 2 cm olduğu için |AC| uzunluğu 2 cm'den büyük olmalıdır. Yukarıda bulduğumuz tam sayılardan 2'den büyük olanlar 3, 4, 5, 6, 7, 8 ve 9'dur.
|AC| için toplam 7 tam sayı değeri bulduğumuz için doğru cevap C'dir.
CEVAP: C
Bir kargo şirketi gönderilen kargonun kilogram cinsinden kütlesi ile desimetreküp cinsinden hacmini hesaplıyor ve hangisine göre kargo ücreti fazla ise o ücreti alıyor. Bu kargo şirketine ait ücret tarifesi Tablo 1 ve Tablo 2'de verilmiştir.
Tablo 1: Kütlelerine Göre Kargo Ücreti
| Kütle (x kg) | Ücret (TL) |
| 0 < x ≤ 3 | 5 |
| 3 < x ≤ 6 | 6,50 |
| 6 < x ≤ 10 | 8 |
Tablo 2: Hacimlerine Göre Kargo Ücreti
| Hacim (y dm3) | Ücret (TL) |
| 0 < y ≤ 9 | 5,50 |
| 9 < y ≤ 18 | 7 |
| 18 < x ≤ 30 | 9 |
Buse bu kargo şirketi ile Tablo 3'te yarıçaplarının uzunlukları, yükseklikleri ve kütleleri verilen dik dairesel silindir şeklindeki kargoları yollamıştır.
Tablo 2: Kargolara Ait Bilgiler
| Kargo | Yarıçapının Uzunluğu (cm) | Yüksekliği (cm) | Kütlesi (kg) |
| 1. kargo | 12 | 20 | 4 |
| 2. kargo | 15 | 18 | 6 |
Buna göre Buse bu kargolar için kaç lira ödeme yapmıştır? (π yerine 3 alınız.)
Tablo 2'deki hacimler desimetreküp cinsinden verilmiştir. Desimetreküp cinsinden hacimler elde edebilmek için kargo ölçülerinin dm'ye çevrilmesi gerekir. (Bir uzunluk cm'den dm'ye çevrilirken 10'a bölünür.)
| Kargo | Yarıçapının Uzunluğu (dm) | Yüksekliği (dm) |
| 1. kargo | 1,2 | 2 |
| 2. kargo | 1,5 | 1,8 |
r taban yarıçapı ve h yükseklik olmak üzere, dairesel dik silindirin hacmi V = (πr2h)'dir.
Kütleye ve hacme göre kargo ücretleri aşağıdaki gibidir.
| Kargo | Kütleye göre ücret (TL) | Hacme göre ücret (TL) |
| 1. kargo | 6,5 | 5,5 |
| 2. kargo | 6,5 | 7 |
1. kargoda kütleye göre ve 2. kargoda hacme göre verilen ücret daha yüksektir. Bu ücretlerin toplamı 6,5 + 7 = 13,5 TL'dir.
CEVAP: D
400 metrelik düz bir yarış pistine başlangıç noktasına uzaklıkları metre cinsinden 2'nin pozitif tam sayı kuvvetleri olacak şekilde yerleştirilebilecek en fazla sayıda engel yerleştiriliyor. Bu pistte 8 atletin yarıştığı bir engelli koşusunda yarışmacılardan biri 20. metrede, bir diğeri 50. metrede yarışı bırakıyor.
Diğer yarışmacılar yarışı tamamladığına göre yarış bittiğinde atletlerin her birinin üzerinden atladığı engel sayılarının toplamı kaçtır?
2'nin 400'den küçük pozitif tam sayı kuvvetleri aşağıdaki gibidir.
Engellerin başlangıç noktasına metre cinsinden uzaklıkları:
Yukarıdaki çıkarımlara göre
Yarışmacıların üzerinden atladıkları toplam engel sayısı 4 + 5 + 6 × 8 = 57'dir.
CEVAP: A