SÜRE
40:002019-2020 LGS MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2019-2020 LGS
SÜRE
40:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
..., ... birer doğal sayı olmak üzere
... dir.
Bir bilye atma oyununa ait, kısa kenar uzunluğu 1 m olan dokuz eş dikdörtgensel bölgeden oluşan oyun parkuru aşağıda verilmiştir.
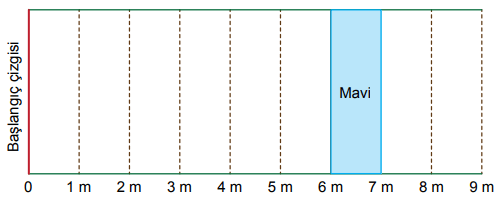
Başlangıç çizgisinden atış yapan bir oyuncunun attığı bilye, parkurda gösterilen mavi bölgede kalmıştır.
Buna göre bu bilyenin başlangıç çizgisine uzaklığı metre cinsinden aşağıdakilerden hangisi olamaz?
Çözüm:
Atılan bilyenin mavi bölgeye düşebilmesi için başlangıç çizgisi ile arasındaki uzaklığın ... metreden düşük ve ... metreden yüksek olmaması gerekir. Seçeneklerdeki uzaklıklar
A) ... ... m,
B) ... ... m,
C) ... ... m ve
D) ... ... m'dir.
... m ile ... m arasında olmayan tek uzaklık ... m'dir.
CEVAP: D
Ayşe’nin bir yılda okuduğu kitapların türlerine göre dağılımı aşağıdaki daire grafiği ile gösterilmiştir.
Grafik: Ayşe’nin Okuduğu Kitapların Türlerinin Dağılımı

Kareli zeminde verilen sütun grafiklerinden hangisi yukarıdaki daire grafiğine uygun oluşturulmuştur?
Daire grafiğinin,
oluşturmaktadır. Kitap türlerinin sayıları, daire grafiğindeki dilimlerin açılarıyla doğru orantılıdır. Her 30⁰'lik kısma 1 birim dediğimizde
olur. Bu sayıları kareli zeminde A seçeneğindeki grafikle gösterebiliriz.
CEVAP: A
Bir ondalık gösterimin, basamak değerleri toplamı şeklinde yazılmasına ondalık gösterimin çözümlenmesi denir.
Bir basketbol takımındaki beş oyuncunun boy uzunluklarının çözümlenmiş şekli aşağıdaki tabloda verilmiştir.
Tablo: Oyuncuların Boylarının Uzunlukları
| İsim | Boy Uzunluğu (cm) |
| Ayça | 2 . 102 + 1 . 100 + 1. 10–1 |
| Beyza | 1 . 102 + 7 . 101 + 5 . 100 + 5 . 10–1 |
| Ceyda | 1 . 102 + 8 . 101 + 4 . 100 |
| Derya | 1 . 102 + 8 . 101 + 7 . 100 + 2 . 10–1 |
| Esra | 1 . 102 + 8 . 101 + 5 . 100 + 6 . 10–1 |
Takımın antrenörü, boyu 185 santimetreden kısa olan oyunculardan birini oyun kurucu olarak oynatacaktır.
Buna göre verilen oyuncular arasında oyun kurucu olarak oynayabilecek kaç oyuncu vardır?
Oyunculardan sadece Beyza ve Ceyda'nın boyu 185 cm'den kısadır. Buna göre, takımda oyun kurucu olarak oynayabilecek 2 oyuncu vardır.
CEVAP: C
..., ..., ... birer doğal sayı olmak üzere
...
... ... dir.
Bir şehrin demir yolu hatları üzerindeki istasyonlar aşağıdaki şekilde noktalar ile gösterilmiştir. Aynı hat üzerinde bulunan ardışık iki istasyon arasındaki mesafeler birbirine eşittir.
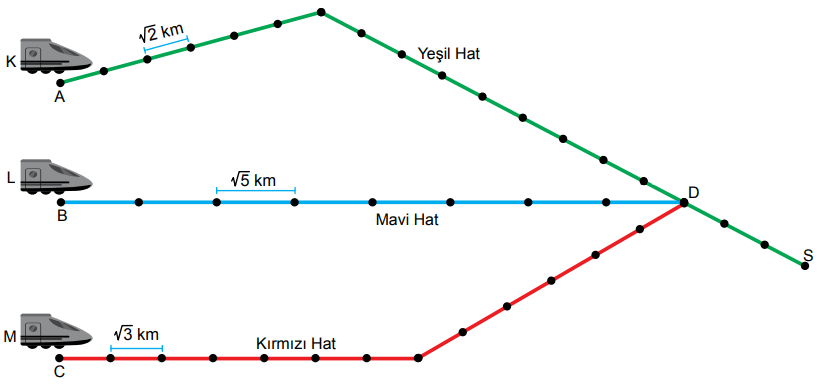
A, B, C istasyonlarından hareket eden K, L ve M trenleri ortak olan D istasyonundan sonra yeşil hattı kullanarak S istasyonuna ulaşıyorlar.
Bu trenlerin gittikleri yolların uzunluğuna göre doğru sıralanışı aşağıdakilerden hangisidir?
D ve S istasyonları arasındaki yol ortak olduğu için trenlerin hareket noktaları ile D istasyonu arasındaki mesafeleri karşılaştırmamız yeterlidir.
A ve D istasyonları arasındaki mesafe (K treni)
... ... km
B ve D istasyonları arasındaki mesafe (L treni)
... ... km
C ve D istasyonları arasındaki mesafe (M treni)
... ... km
... > ... > ... olduğundan doğru cevap M > K > L'dir.
CEVAP: D
Kenarlarının uzunlukları x metre ve 2x metre olan dikdörtgen şeklindeki oyun parkının planı Şekil I’de verilmiştir. Bu oyun parkının kenarları 2’şer metre uzatılarak Şekil II’deki gibi dikdörtgen biçiminde bir oyun parkı planlanmıştır.

Buna göre Şekil II’deki oyun parkının alanının Şekil I’deki oyun parkının alanından kaç metrekare fazla olduğunu veren cebirsel ifade aşağıdakilerden hangisidir?
Şekil II'deki oyun parkının kenar uzunlukları 2x + 2 ve x + 2 m'dir. Alanı ise
(2x + 2)(x + 2) = 2x . x + 2x . 2 + 2 . x + 2 . 2
=2x2 + 6x + 4 m2'dir.
Bu iki alan arasındaki fark
2x2 + 6x + 4 – 2x2 = 6x + 4 m2'dir.
CEVAP: A
Yükseklikleri santimetre cinsinden birer tam sayı olan aşağıdaki dikdörtgenler prizması şeklindeki kutuların her birinden üçer adet vardır.
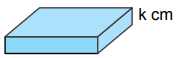
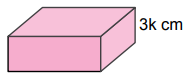
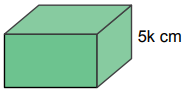

Bu kutular aşağıdaki gibi üst üste dizilerek üç ayrı blok oluşturulmuştur.



Bloklardaki kutuların yerleri değiştirilmeden bu üç blok üst üste konularak bir kule oluşturuluyor. Daha sonra kulenin en üstünde bulunan kutu alınıyor.
Son durumda bu kulenin yüksekliğinin santimetre cinsinden değeri aşağıdakilerden hangisi olamaz?
Kule oluşturulurken 4 çeşit kutunun her birinden 3'er tane kullanılmaktadır. Bu kutuların toplam yüksekliği
3(k + 3k + 5k + 7k) = 3 . 16k = 48k cm'dir.
Sorudaki blokların en üstündeki kutular k, 5k ve 7k yüksekliğindedir. Kule oluşturulurken bloklardan hangisinin en üstte olduğuna bağlı olarak bu kutulardan biri alınmaktadır.
k bir tam sayı olduğuna göre kulenin yüksekliği 47, 43 veya 41'e tam bölünmektedir. 90, bu sayılardan hiçbirine tam bölünmediği için santimetre cinsinden kulenin yüksekliği olamaz.
CEVAP: B

Aşağıdaki tabloda • (nokta) ve – (çizgi) karakterleri kullanılarak tanımlanmış rakamlar verilmiştir.
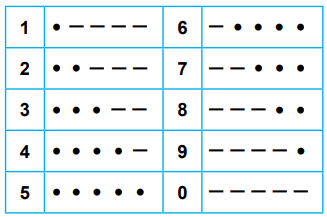
Bu rakamlara karşılık gelen karakterlerle oluşturulan iki basamaklı doğal sayıların tamamı aşağıdaki gibi özdeş kartlara yazılıp boş bir torbaya atılmıştır.
Örneğin,

Bu torbadan rastgele yapılan bir çekilişte üzerindeki • (nokta) sayısı 5 olan kartın çekilme olasılığı kaçtır?
İki basamaklı 90 doğal sayı vardır. Bu doğal sayıların 17'sinde (50, 14, 41, 16, 61, 94, 49, 96, 69, 27, 72, 38, 83, 87, 78, 23, 32) beş nokta bulunmaktadır. Buna göre istenilen olasılık ...'dır.
CEVAP: C
Aşağıda her birinin kütlesi 3 g olan sarı boncuklardan ve her birinin kütlesi 5 g olan mavi boncuklardan yeterli sayıda verilmiştir. Bu boncuklar kullanılarak bir kolye yapılmıştır.

Kolyedeki mavi boncukların toplam kütlesi sarı boncukların toplam kütlesine eşittir.
Kullanılan boncukların toplam kütlesi 230 gramdan az olduğuna göre bu kolyedeki sarı boncukların sayısı ile mavi boncukların sayısı arasındaki fark en fazla kaçtır?
3 gramlık boncukların toplam kütlesi 3'e ve 5 gramlık boncukların toplam kütlesi 5'e kalansız bölünür. Bu kütleler birbirine eşit olduğundan farklı renk boncukların gram cinsinden kütleleri hem 3'e hem de 5'e kalansız bölünür. Hem 3'e hem de 5'e kalansız bölünen sayılar EKOK(3, 5) = 15'in tam katıdır. Buna göre kolyede kullanılan boncukların toplam kütlesi 15 + 15=30'un tam katıdır. 230'dan küçük ve 30'un tam katı olan en büyük doğal sayı 210'dur. Toplam kütle 210 gram olduğunda hem sarı hem de mavi boncukların kütlesi 210 ÷ 2 = 105 gram olur. Bu durumda kullanılan
Boncuk sayıları arasındaki fark 35 – 21 = 14'tür.
CEVAP: A
Aşağıda dört farklı renkteki kartların her birinden üçer adet verilmiştir. Aynı renkteki kartların üzerinde aynı kareköklü ifade yazmaktadır
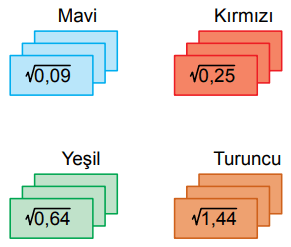
Eymen, bu kartlardan seçerek üstlerinde yazan kareköklü ifadeleri topladığında bir doğal sayı elde etmektedir.
Buna göre Eymen en fazla kaç kart seçmiştir?
Mavi kartlardaki sayı
... ...
Kırmızı kartlardaki sayı
... ...
Yeşil kartlardaki sayı
... ...
Turuncu kartlardaki sayı
... ...
Tüm kartlardaki sayıların toplamı
3(0,3 + 0,5 + 0,8 + 1,2) = 8,4'tür.
8,4'ten kartlardaki sayılardan yalnız biri çıkarılarak bir doğal sayı elde edilemez. İki turuncu kart çıkarıldığında ise toplam sayı 6 olur.
8,4 – 2 × 1,2 = 6
12 karttan 2'si çıkarıldığında geriye 10 kart kalır. Buna göre, Eymen en fazla 10 kart seçmiştir.
CEVAP: C
... ve ..., ... tam sayılar olmak üzere
... ve ... dir.
Bir kenarının uzunluğu 54 cm olan kare şeklindeki kâğıdın bir yüzüne aşağıdaki gibi 12 eş dikdörtgen ve 1 kare çizilmiştir. Bu şekillerden kare ve 2 eş dikdörtgen kırmızıya boyanmıştır

Buna göre kırmızı bölgelerin alanları toplamı kaç santimetrekaredir?
Dikdörtgenin kısa kenar uzunluğuna x dersek
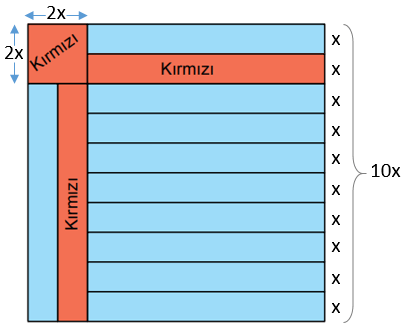
Soruda kare şeklinde olduğu belirtildiği için kâğıdın genişliği de 10x'tir. Buna göre dikdörtgenin uzun kenarı 10x – 2x = 8x'tir.

Santimetrekare cinsinden karenin alanı (2x)2 = 4x2 ve dikdörtgenin alanı x . 8x = 8x2'dir. Dolayısıyla, boyalı bölgelerin toplam alanı santimetrekare cinsinden
4x2 + 2 . 8x2 = 20x2'dir.
10x'i 54'e eşitleyerek x'in değerini bulabiliriz.
10x = 54
⇒ x = ... cm
20x2 ifadesinde x'in değerini yerine yazdığımızda 57 sonucunu elde ederiz.
20x2 = ... = 5 . 56 = 57 cm2
CEVAP: B
Dikdörtgen şeklindeki bir kâğıt, alanları santimetrekare cinsinden 10’dan büyük birer tam kare pozitif tam sayıya eşit olan karesel bölgelere aşağıdaki gibi ayrılmıştır.
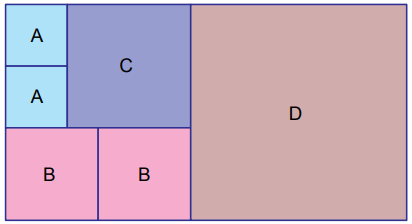
Eşit alanlı bölgeler aynı harf ile gösterildiğine göre dikdörtgen şeklindeki bu kâğıdın bir yüzünün alanı en az kaç santimetrekaredir?

10'dan büyük tam kare sayıların en küçüğü 16 olduğu için en küçük kare olan A'nın alanı en az 16 cm2'dir. Bu durumda, A'nın kenar uzunluğu ... cm ve C'nin kenar uzunluğu 4 + 4 = 8 cm olur.
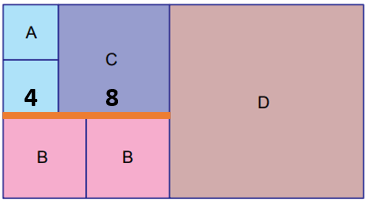
A ve C'nin kenar uzunluklarının toplamı B'nin kenar uzunluğunun 2 katına eşittir. Dolayısıyla, B'nin kenar uzunluğu (4 + 8) ÷ 2 = 6 cm'dir.

D'nin kenar uzunluğu 8 + 6 = 14 cm'dir.
Yukarıda bulduğumuz kenar uzunluklarına göre toplam alan 364 cm2'dir.
42 + 42 + 82 + 62 + 62 + 142 = 364 cm2
CEVAP: C
Alanı 1050 cm2 olan kare şeklindeki bir panoya kenarlarından birinin uzunluğu 5’in tam sayı kuvveti, diğerinin uzunluğu 2’nin tam sayı kuvveti olan dikdörtgen şeklindeki bir afiş, pano yüzeyinden taşmayacak şekilde asılacaktır.
Buna göre afişin bir yüzünün alanı en fazla kaç santimetrekaredir?
a ve b birer tam sayı olmak üzere, afişin kenar uzunlukları santimetre cinsinden 5a ve 2b şeklinde gösterilebilir.
Panonun kenar uzunluğu ... cm'dir. Afişin panodan taşmaması için santimetre cinsinden kenar uzunluklarının ...'den büyük olmaması gerekir.
5a ≤ ...
2b ≤ ...
Yukarıda elde ettiğimiz sonuçlara göre afişin alanı en fazla 52 × 25 = 25 × 32 = 800 cm2 olabilir.
CEVAP: B
Bir lokantada hazırlanan yemek çeşitleri ve porsiyon sayıları sütun grafiği ile bu yemekler için kullanılan toplam 60 g tuzun yemek çeşitlerine göre dağılımı daire grafiği ile aşağıda gösterilmiştir. Bir çeşit yemeğin her porsiyonunda eşit miktarda tuz bulunmaktadır.

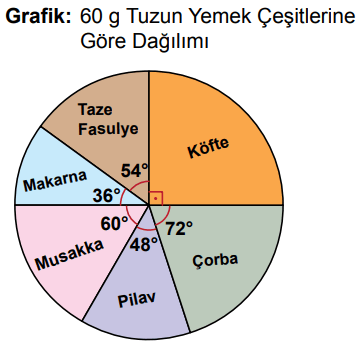
Bu lokantada üç farklı yemekten birer porsiyon yiyen bir müşteri toplam 5 g tuz tüketmiştir
Buna göre bu müşterinin yediği yemekler aşağıdakilerden hangisidir?
Daire grafiğinde 60 gram tuz 360⁰ ile gösterildiği için bu grafikteki her 360⁰ ÷ 60 = 6⁰'lik merkez açı, 1 gram tuza karşılık gelmektedir. Buna göre, bir yemek çeşidindeki toplam tuz miktarı, bu yemeği gösteren merkez açının 6'da 1'i kadardır.
Bir yemek çeşidindeki toplam tuz miktarı porsiyon sayısına bölünerek bu yemek çeşidinin bir porsiyonundaki tuz miktarı bulunabilir.
Toplamları 5 g olan farklı yemekler pilav, taze fasulye ve köftedir.
2 + 1,5 + 1,5 = 5 g
CEVAP: D


Kenarlarının uzunlukları 1 m ve 9 m olan dikdörtgen biçimindeki bir halının ön yüzü, şekildeki gibi farklı renklere boyanmıştır. Bu renklerin her birinin kapladığı karesel bölgenin alanı birbirine eşittir.
Bu halı, parçalarda aynı renk olmayacak şekilde iki parçaya bölünecektir.
Buna göre bu parçalardan birinin boyalı yüzünün alanının, diğerinin boyalı yüzünün alanının 2 katı olması olasılığı kaçtır?
9 renkten oluşan bu halı 8 farklı şekilde bölünebilir. Bu bölünme şekillerinden 2'sinde, parçalardan birinin alanı diğerinin alanının 2 katıdır.
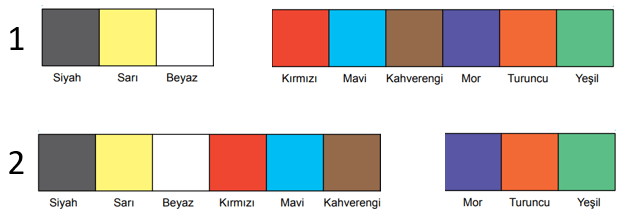
Buna göre istenilen olasılık ...'tür.
CEVAP: B
Aşağıda çevresinin uzunluğu (2x + 2) m olan dikdörtgenlerden yeterli sayıda verilmiştir.

Bu dikdörtgenler [AB] boyunca sırasıyla önce uzun kenarı sonra kısa kenarı üzerine aralarında boşluk kalmayacak şekilde aşağıdaki gibi yerleştirilmiştir. Uzun kenarı üzerine yerleştirilen ilk dikdörtgenin bir köşesi A noktası ile kısa kenarı üzerine yerleştirilen son dikdörtgenin bir köşesi B noktası ile çakışıktır.

Bu dikdörtgenler (x + 1) kez kısa kenarı üzerine yerleştirildiğine göre [AB]’nın uzunluğunu metre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
... kez kısa kenarı üzerine yerleştirilen bu dikdörtgen, ... kez de uzun kenarı üzerine yerleştirilmiştir. Bu nedenle, A ve B noktaları arasındaki mesafe, ... kısa kenarla ... uzun kenarın toplam uzunluğuna eşittir. Bir dikdörtgenin 1 kısa kenarı ile 1 uzun kenarının toplamı, çevresinin yarısıdır. Dolayısıyla, A ile B arasındaki uzaklık ... tane çevreye eşittir.
... ... ... ...
CEVAP: D

Renkleri dışında özdeş olan toplardan 4’ü kırmızı, geri kalanı beyazdır. Bu topların tamamı aşağıdaki boş A, B ve C torbalarına dağıtılıyor.

Bu torbaların her birinden rastgele çekilen bir topun kırmızı olma olasılığı birbirine eşittir.
Buna göre başlangıçtaki beyaz top sayısı aşağıdakilerden hangisi olamaz?
Torbalardan birine hiç kırmızı top atılmamış olsaydı, bu torbadan çekilen topun kırmızı olma olasılığı 0 olurdu. Yalnız bu durumda, torbalardan rasgele çekilen topların kırmızı olma olasılıkları birbirine eşit olamazdı. Bu nedenle her torbaya en az 1 kırmızı top atılmıştır.
4 kırmızı top 3 torbaya her birinde en az 1 kırmızı top olacak şekilde dağıtıldığında, torbalardan ikisine birer tane ve birine iki tane kırmızı top düşer. Kırmızı top çekme olasılıklarınıın eşit olabilmesi için 1 kırmızı top atılan torbalarda eşit sayıda ve 2 kırmızı top atılan torbaya diğerlerinin 2 katı kadar beyaz top eklenmesi gerekir.
İçinde 1 kırmızı top olan torbalardaki beyaz top sayısına x dersek içinde 2 kırmızı top olan torbadaki beyaz top sayısı 2x olur. Buna göre beyaz topların toplam sayısı x + x + 2x = 4x şeklinde ifade edilebilir. x bir doğal sayı olduğundan 4x sayısı 4'e kalansız bölünür. Seçeneklerdeki 82 sayısı 4'e kalansız bölünmediği için beyaz topların toplam sayısı 82 olamaz.
CEVAP: B
Her birinin kütlesi 40 kg’dan az ve birbirine eşit olan buğday çuvalları aşağıdaki gibi bir kantarda tartıldığında çuvalların toplam kütlesi 720 kg gelmektedir.

Kantar üzerindeki çuvalların sayısı, bu çuvallarla eşit kütleye sahip çuvallar konularak arttırıldığında toplam kütle 1344 kg olmaktadır

Buna göre kantar üzerine sonradan konulan çuvalların sayısı en az kaçtır?
Bir çuvalın kilogram cinsinden kütlesi hem 720'nin hem de 1344'ün bölenidir.

EBOB(720, 1344) = 2 . 2 . 2 . 2 . 3 = 48 olduğundan 720 ve 1344 sayılarının ortak bölenleri 48'in bölenlerine eşittir. 40'tan küçük ortak bölenlerin en büyüğü 24 olduğu için çuvalların kütlesi en fazla 24 kg olabilir.
Kantara sonradan eklenen kütle 1344 – 720 = 624 kg'dır. Bu kütle en az 624 ÷ 24 = 26 çuvaldır.
CEVAP: C
... ve ..., ... tam sayılar olmak üzere
... ve ...
...
Bir fabrikada üretilen mavi ve kırmızı renkli otomobiller bir galeriye iki tır ile taşınmaktadır.
Bu otomobillerin birer adedinin kütleleri Tablo 1’de, tırların taşıdığı otomobillerin sayıları Tablo 2’de gösterilmiştir.


A tırı ile taşınan mavi ve kırmızı otomobillerin sayıları birbirine eşittir
İki tırın taşıdığı otomobillerin toplam kütlesi 214 kg olduğuna göre A tırı ile taşınan otomobil sayısı kaçtır?
Mavi otomobilllerin kütlesini 2 tabanında 45=(22)5 = 210 kg şeklinde ifade edebiliriz.
A tırı ile taşınan mavi otomobillerin sayısını n ile gösterdiğimizde bu tırda taşınan toplam kütle
n . 210 + n . 211 = n . 210 + 2n . 210 = 3n . 210 kg
olur. B tırında taşınan toplam kütle ise
4 . 210 + 3 . 211 = 4 . 210 + 6 . 210 = 10 . 210 kg'dır.
A ve B tırlarının taşıdığı toplam kütle
3n . 210 + 10 . 210 = (3n + 10) . 210 kg'dır.
Bu kütleyi 214 kg'a eşitleyerek n sayısını bulabiliriz.
(3n + 10) . 210 = 214
⇒ (3n + 10) . 210 = 24 . 210
⇒ 3n + 10 = 24
⇒ 3n + 10 = 16
⇒ 3n = 6
⇒ n = 2
Buna göre A tırında taşınan otomobil sayısı 2 + 2 = 4'tür.
CEVAP: B
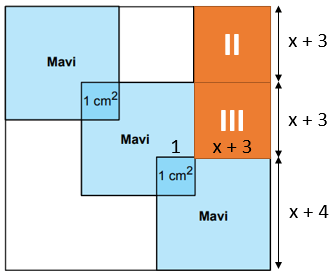
Kare şeklindeki boş bir panoya kare şeklindeki üç eş mavi karton, köşegenleri panonun köşegeni ile çakışacak şekilde aşağıdaki gibi yerleştirilmiştir.

Panoda boş bırakılan bölgelerin alanları toplamı 6x2 + 36x + 54 santimetrekaredir. Kartonların üst üste gelen bölgelerinin her biri, alanları 1 cm2 olan karesel bölgelerdir.
Buna göre panonun çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Panoda boş bırakılan bölgelerin toplam alanı santimetrekare cinsinden
6x2 + 36x + 54 = 6(x2 + 6x + 9) = 6(x + 3)2'dir.

Boş kalan bölgeler yukarıdaki gibi 6 eş kareye ayrılabilir. Bu karelerden her birinin alanı 6(x + 3)2 ÷ 6 = (x + 3)2 cm2 ve kenar uzunluğu x + 3 cm'dir. Mavi karenin kenar uzunluğu, bu uzunluktan 1 cm fazladır. Buna göre panonun kenar uzunluğu x + 3 + x + 3 + x + 4 = 3x + 10 cm'dir.
Panonun çevresi, kenar uzunluğunun 4 katıdır.
4(3x + 10) = 12x + 40 cm
CEVAP: A
Bir okulun Ordu iline düzenleyeceği gezide ziyaret edilecek yerlerle ilgili yapılan anket çalışmasında her bir öğrenci ziyaret edilebilecek yerlerle ilgili yalnız bir tercihte bulunmuştur. Bu anketin sonuçları sütun grafiği ile ankete katılan kız ve erkek öğrencilerin sayılarının dağılımı daire grafiği ile aşağıda gösterilmiştir.


Ankete katılan kız ve erkek öğrencilerin sayılarının ziyaret etmek istedikleri yere göre dağılımları aşağıdaki daire grafiklerinde gösterilmiştir.

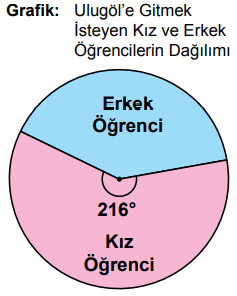

Yukarıda verilenlere göre Boztepe’yi ziyaret etmek isteyen erkek öğrencilerin sayısı kaçtır?
Sütun grafiğinde verilen bilgilere göre ankete katılan öğrenci sayısı 30 + 15 + 10 + 5 = 60'tır.
Daire grafiğindeki dilimlere göre 60 öğrencinin ...'i kızdır. Ayrıca
Buna göre, Boztepe'yi ziyaret etmek isteyen kız öğrenci sayısı 25 – (12 + 9 + 3) = 1'dir. Boztepe'ye toplam 5 öğrenci gitmek istediği için bu öğrencilerden 5 – 1 = 4'ü erkektir.
CEVAP: D