SÜRE
40:002020-2021 LGS MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2020-2021 LGS
SÜRE
40:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
Kare şeklindeki bir arsada kenar uzunluğu x m olan kare şeklinde bir bölge spor sahası, kenar uzunluğu y m olan kare şeklinde bir bölge de çay bahçesi olarak aşağıdaki gibi planlanmıştır. Kalan bölgeler ise çocuk parkı olarak ayrılmıştır.
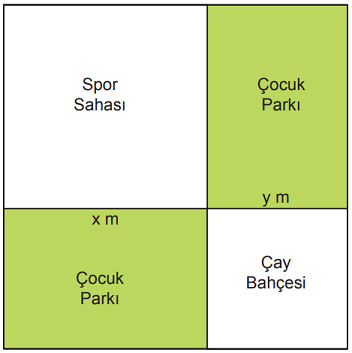
Buna göre çocuk parkı olarak ayrılan bölgelerin alanları toplamını metrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
Spor sahası ve çay bahçesi kare şeklinde olduğu için çocuk parklarının kenar uzunlukları x ve y metredir.
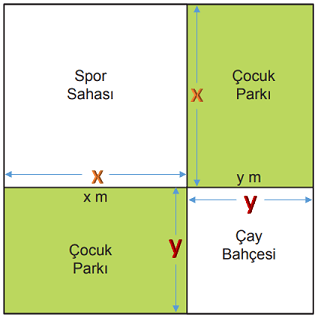
Buna göre, çocuk parklarından her birinin alanı xy m2 ve soruda istenilen toplam alan xy + xy = 2xy m2'dir.
CEVAP: B
..., ... birer doğal sayı olmak üzere
... dir.
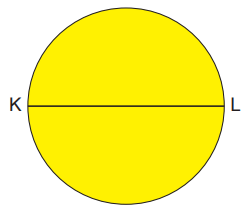

Yukarıda, çapı KL doğru parçası olan daire şeklinde bir karton ve eş bölmelere ayrılmış 10 santimetrelik bir cetvel verilmiştir. KL doğru parçası, K noktası 2'ye karşılık gelecek şekilde cetvelin kenarı ile çakıştırıldığında L noktası 6 ile 7 arasında, 7'ye daha yakın bir noktaya karşılık gelmektedir.
Buna göre KL doğru parçasının uzunluğu, santimetre cinsinden aşağıdakilerden hangisi olabilir?
Cetvel 2 birim sağa kaydırıldığında K noktası 0'a ve L noktası 4 ile 5 arasında 5'e daha yakın bir noktaya karşılık gelir. Bu nokta, KL doğru parçasının santimetre cinsinden uzunluğunu gösterir.
... formundaki bir ifadenin 4 ile 5 arasında ve 5'e daha yakın olabilmesi için ...'nın 42 = 16 ile 52 = 25 arasında ve 25'e daha yakın olması gerekir. Seçeneklerdeki katsayıları karekök içerisine alarak ifadelerden hangisinin bu şartları sağladığını görebiliriz.
A) ... ... → 4 ile 5 arasında ve 4'e daha yakın
B) ... ... → 4 ile 5 arasında ve 5'e daha yakın
C) ... ... → 5 ile 6 arasında ve 5'e daha yakın
D) ... ... → 6 ile 7 arasında ve 7'ye daha yakın
CEVAP: B
Dikdörtgen şeklindeki bir kâğıt aşağıdaki gibi kısa kenarlarına paralel olarak kesildiğinde dikdörtgen şeklinde iki parça elde edilmiştir.

Elde edilen bu parçalar kısa kenarlarına paralel olarak tekrar kesildiğinde aşağıdaki gibi birbirine eş ikişer kare oluşmuştur. Bu karelerden her birinin bir kenar uzunluğu santimetre cinsinden birer doğal sayıdır.
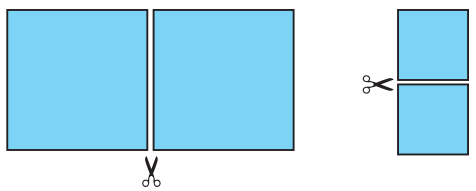
Buna göre başlangıçtaki kâğıdın bir yüzünün alanı santimetrekare cinsinden aşağıdakilerden hangisi olamaz?

Oluşturulan küçük karelerin kenar uzunluklarına x cm dersek , büyük karelerin kenar uzunlukları 2x cm olur. Dolayısıyla, santimetrekare cinsinden
şeklinde ifade edilebilir. Buna göre, başlangıçtaki kâğıdın bir yüzü
x2 + x2 + 4x2 + 4x2 = 10x2 cm2
çıkar. x bir doğal sayı olduğundan x2 bir tam karedir. 10x2 ifadesi ise bir tam karenin 10 katıdır. Bir tam karenin 10 katı olmayan tek seçenek 240'tır. 240 sayısı, santimetrekare cinsinden başlangıçtaki kâğıdın bir yüzünün alanı olamaz.
CEVAP: D
Aşağıdaki tabloda Ordu, Giresun ve Trabzon şehirlerini ziyaret eden turistlerin sayıları verilmiştir.
Tablo: Şehirleri Ziyaret Eden Turistlerin Sayıları
| Şehirler | Turist Sayısı |
| Ordu | 0,125 . 106 |
| Giresun | 9,5 . 104 |
| Trabzon | x . 107 |
Trabzon'u ziyaret eden turistlerin sayısı, Ordu'yu ziyaret eden turistlerin sayısından az ve Giresun'u ziyaret eden turistlerin sayısından fazladır.
Buna göre x'in alabileceği değerlerden biri aşağıdakilerden hangisidir?
Ordu'yu ziyaret eden turist sayısı
0,125 . 106 = 125 000 ve
Giresun'u ziyaret eden turist sayısı
9,5 . 104 = 95 000'dir.
Trabzon'u ziyaret eden turist sayısı ise 95 000 ile 125 000 arasındadır. x sayısı 10–2 değerini aldığında x . 107 ifadesi istenilen aralıkta çıkar.
CEVAP: C
Uzun kenarlarının uzunlukları birbirine eşit, kısa kenarlarının uzunlukları 20 cm ve 8 cm olan dikdörtgen şeklinde iki karton Şekil I'de verilmiştir.
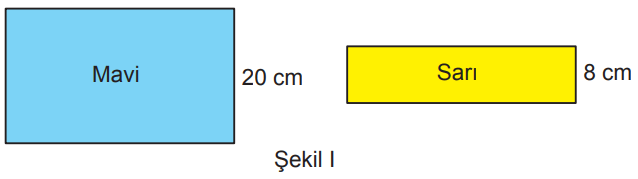
Bu kartonlar Şekil II'deki gibi uzun kenarları paralel olacak ve sarı karton altta kalacak biçimde üst üste yerleştirildiğinde mavi dikdörtgenin uzun kenarı, sarı dikdörtgeni iki eş parçaya ayırmakta ve eş parçalardan biri mavi dikdörtgenin altında kalmaktadır.
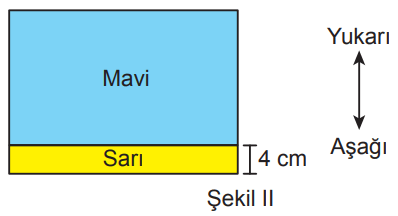
Buna göre x'in alabileceği değerleri santimetre cinsinden gösteren eşitsizlik aşağıdakilerden hangisidir?
x'in alabileceği
karşılaşılır.
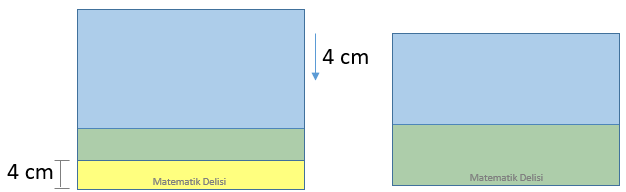
Alt kenarların çakışabilmesi için mavi kartonun 4 cm aşağı kaydırılması gerekir.
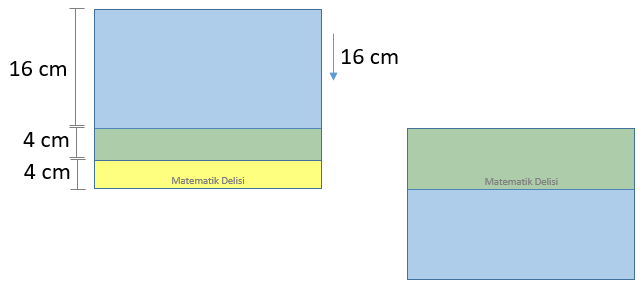
Üst kenarların çakışması için de mavi kartonun 16 cm aşağı kaydırılması gerekir.
Sonuç olarak, x'in alabileceği en düşük ve en yüksek değerler sırasıyla 4 ve 16'dır.
4 ≤ x ≤ 16
CEVAP: A
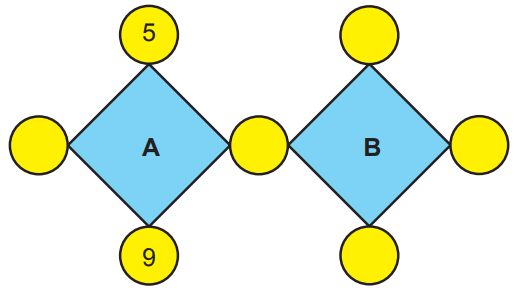
Yukarıdaki şekilde verilen her bir dairenin içine birbirinden farklı birer doğal sayı yazılacaktır. Bu sayılardan ikisi şekilde verilmiştir. Bulundukları dörtgenin köşelerindeki dairelerde yazan dört sayının çarpımına eşit olan A ve B sayıları aralarında asaldır.
Buna göre A + B en az kaçtır?
Çözümü daha iyi takip edebilmek için verilen boşlukları isimlendirelim.
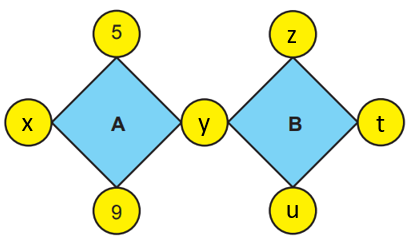
y sayısı hem A hem de B'nin köşesinde olduğundan iki sayının da çarpanıdır. Yalnız, aralarında asal olan A ve B sayılarının tek ortak çarpanı 1'dir. Bu nedenle y = 1 olmalıdır.
A + B'nin en düşük değerini aradığımız için diğer boşluklara da mümkün olduğunca küçük sayılar yazmamız gerekir. 2, 3 ve 4 sayılarını bu boşluklara yerleştirmeye çalışalım.
A'nın alt köşesinde 9 olduğu için bu sayı 9'a ve dolayısıyla 3'e kalansız bölünür. z, t veya u yerine 3 yazmamız, B'yi de 3'e bölünebilir yapar. Bu durumda A ve B aralarında asal olmaz. Dolayısıyla 3'ü yalnızca x yerine yazabiliriz. z ve t'nin bulunduğu dairelere de 2 ve 4 sayılarını yerleştirebiliriz.
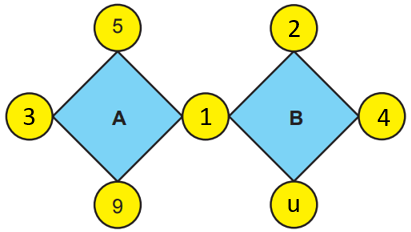
Şimdi de geriye kalan son boşluğa yazabileceğimiz en küçük sayıyı bulalım. Halihazırda A'nın çarpanlarından biri 5 olduğu için bu sayıyı u yerine yazamayız. 6 sayısı ise 3'e kalansız bölünür. Bu nedenle, u yerine 6 yazmamız A ile B'nin aralarında asal olmasını engeller. Yalnız, şekildeki herhangi bir sayı 7'nin tam katı olmadığı için u yerine 7 yazabiliriz.
Yukarıda bulduğumuz sayıları kullandığımızda A'nın 135'e ve B'nin 56'ya eşit olduğunu görebiliriz.
A = 3 . 5 . 1 . 9 = 135
B = 1 . 4 . 7 . 2 = 56
Buna göre A + B toplamı en az 191'dir.
135 + 56 = 191
CEVAP: B
... ve ..., ... tam sayılar olmak üzere
... ve ...
Aşağıda, her bir hücresinde 2'nin birbirinden farklı tam sayı kuvvetlerinin yazılı olduğu iki sütunlu bir tablo verilmiştir. Tabloda bu üslü ifadelerden ikisi E ve F harfleriyle gösterilmiştir.
| I. Sütun | II. Sütun |
| 2–1 | 2–2 |
| E | F |
| 23 | 21 |
I.sütundaki üç üslü ifadenin çarpımı tam kare pozitif bir tam sayıya ve II. sütundaki üç üslü ifadenin çarpımı da tam kare pozitif bir tam sayıya eşittir.
Buna göre E + F en az kaçtır?
Tablodaki E ve F sayılarını sırasıyla 2e ve 2f şeklinde gösterdiğimizde
1. sütundaki sayıların çarpımı
2–1 . 2e . 23 = 2–1 + e + 3 = 2e + 2'ye ve
2. sütundaki sayıların çarpımı
2–2 . 2f . 21 = 2–2 + f + 1 = 2–1 + f'ye eşit çıkar.
Bu ifadelerin tam kare olabilmesi için kuvvetlerinin 0 veya pozitif çift sayı olması gerekir. Buna göre e + 2 ve –1 + f sayıları ya 0 ya da pozitif çift sayıdır. Bu şartı sağlayan
Tablodaki sayıların birbirinden farklı olması gerektiği için e kuvveti –2 değerini ve f kuvveti 1 veya 3 değerini alamaz. Buna göre, e'nin alabileceği en küçük değer 0 ve f'nin alabileceği en küçük değer 5'tir. e = 0 ve f = 5 için E + F toplamı 33'e eşittir.
E + F = 20 + 25 = 1 + 32 = 33
CEVAP: A
Aşağıdaki yakıt göstergelerinde ibrenin ucu 0'ı gösterdiğinde yakıt deposunun tamamının boş olduğu, 1'i gösterdiğinde tamamının dolu olduğu ve 0 ile 1 arasına eşit aralıklarla konulan çizgilerden herhangi birini gösterdiğinde ise kaçta kaçının dolu olduğu anlaşılmaktadır.
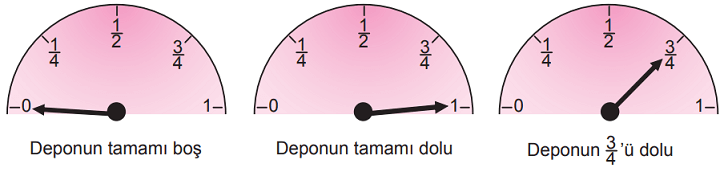
Deposu 48 litre yakıt alabilen bir aracın başlangıçta deposunda 30 litre yakıt bulunmaktadır. Bu araç x litre yakıt tükettikten sonra yakıt göstergesindeki ibrenin ucu ... ile ... arasındaki bir değeri göstermektedir.
Buna göre aracın tükettiği yakıt miktarını litre cinsinden gösteren eşitsizlik aşağıdakilerden hangisidir?
Deposu 48 litre yakıt alan bir araçta ibrenin ucu ... ile ... arasını gösteriyorsa, bu depodaki yakıt miktarı ... L ile ... L arasındadır. Bu miktar 30 – x'e aittir. Çünkü depodaki 30 litre yakıtın x litresi kullanıldığında geriye 30 – x litre yakıt kalır. Dolayısıyla depoda kalan yakıt miktarı aşağıdaki eşitsizlikle gösterilebilir.
12 < 30 – x < 24
Bu eşitsizlikteki tüm taraflardan 30 çıkarıldığında ortada yalnız –x kalır.
12 – 30 < 30 – x – 30 < 24 – 30
⇒ –18 < –x < –6
Tüm taraflar –1 ile çarpıldığında harcanan yakıt miktarını gösteren eşitsizlik elde edilir.
⇒ (–1) . (–18) > (–1) . (–x) > (–1) . (–6)
⇒ 18 > x > 6
⇒ 6 < x < 18
CEVAP: D
Dikdörtgen şeklindeki bir koşu parkuru ve bu parkurun uzun kenarı üzerine yerleştirilmiş dikdörtgen şeklindeki K, L, M ve N tribünleri aşağıda modellenmiştir. Modele göre bitiş çizgisi ile N tribününün kenarlarından biri doğrusaldır. Bu tribünlerin birer kenarlarının ve aralarındaki uzaklıklar aşağıda gösterilmiştir.

Bu parkurun uzun kenarlarına paralel olan sarı çizgi üzerinde bitiş çizgisine doğru koşan iki sporcudan biri K tribünü karşısından geçerken öndeki sporcuyla arasında 46 m mesafe vardır.
Buna göre öndeki sporcunun konumu ile ilgili aşağıdakilerden hangisi kesinlikle yanlıştır?
K ve L tribünlerinin birbirine en uzak noktaları arasında kalan mesafe
25 + 4 + 32 = 32 + 4 + 9 = 45 m'dir.

Buna göre, arkadaki sporcu K tribünün başlangıç noktasında olsa dahi öndeki sporcu L tribününün karşısında olamaz.
CEVAP: D
Bir fırında çavdar ve buğday unları karıştırılarak ekmek yapımında kullanılan bir un elde edilmektedir. Bu undaki çavdar ve buğday unu miktarları arasındaki ilişki aşağıdaki doğrusal grafikte gösterilmiştir.
Grafik: Çavdar ve Buğday Unu Miktarları
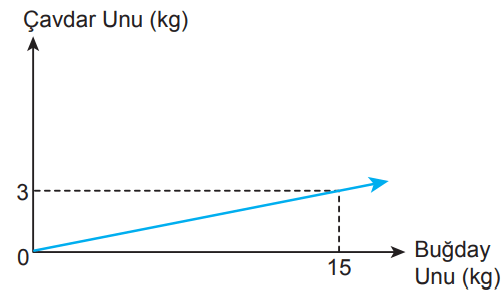
Bir fırında yanlışlıkla çavdar yerine buğday, buğday yerine çavdar unu kullanılarak 120 kg un hazırlanmıştır. Hazırlanan una sadece buğday unu eklenerek çavdar ve buğday unu miktarları arasındaki doğrusal ilişkinin grafiğe uygun hale getirilmesi sağlanacaktır.
Buna göre, hazırlanan una kaç kilogram daha buğday unu eklenmelidir?
Soruda verilen grafiğe göre ekmeklerde kullanılan buğday ununun kütlesi, çavdar ununun kütlesinin 15 ÷ 3 = 5 katıdır. Dolayısıyla, ekmek için hazırlanan her 6 kg unun 1 kg'ı çavdar ve geriye kalan 5 kg'ı buğday unu olmalıdır.
Yanlış hazırlanan unda 120 ÷ 6 = 20 kg çavdar ve 120 – 20 = 100 kg buğday unu kullanılması gerekirken, 100 kg çavdar ve 20 kg buğday unu kullanılmıştır. Doğru karışımda 100 kg çavdara karşılık 100 × 5 = 500 kg buğday unu kullanılması gerekir. Halihazırda 20 kg unu olduğu için eklenmesi gereken miktar 500 – 20 = 480 kg'dır.
CEVAP: C
Dikdörtgen şeklindeki bir kâğıt aşağıdaki gibi altı dikdörtgensel bölgeye ayrılmış ve bu bölgelerden bazılarının alanları şekil üzerinde gösterilmiştir.

Elde edilen bu dikdörtgensel bölgelerden her birinin kenarlarının uzunlukları santimetre cinsinden 1'den büyük birer doğal sayıdır.
Buna göre bu kâğıdın bir yüzünün alanı, santimetrekare cinsinden aşağıdakilerden hangisi olabilir?
Soruda verilen birimler temel alındığında dikdörtgensel bölgelerin kenar uzunlukları, alanlarının 1'den büyük çarpanları olur.
35 ve 21 sayılarının 1'den büyük tek ortak çarpanı 7'dir. Buna göre, alanı 35 cm2 ve 21 cm2 olan bölgelerin ortak kenar uzunluğu 7 cm'dir. Bu bölgelere ait diğer kenar uzunlukları ise 35 ÷ 7 = 5 cm ve 21 ÷ 7 = 3 cm'dir.
Benzer şekilde, 44 ve 33'ün 1'den büyük tek ortak çarpanı 11'dir. Dolayısıyla, alanı 44 cm2 ve 33 cm2 olan bölgelerin ortak kenar uzunluğu 11 cm'dir.
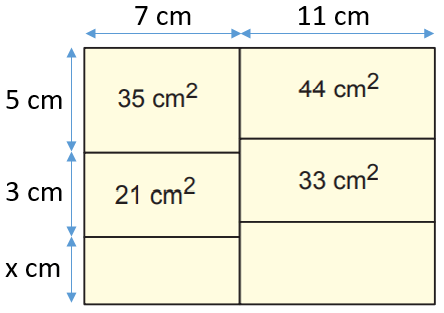
Bulduğumuz kenar uzunluklarını yerlerine yazdığımızda kâğıdın genişliğinin 7 + 11 = 18 cm olduğunu görebiliriz. Ayrıca, sol alttaki bölgenin yüksekliğine x dersek, kâğıdın yüksekliği toplam 8 + x çıkar. x, 1'den büyük bir tam sayı olduğu içi kâğıdın yüksekliği en az 8 + 2 = 10 cm'dir. Buna göre, bir yüzün alanı en az 18 . 10 = 180 cm2'dir.
CEVAP: C
Dik üçgenlerde, 90⁰ lik açının karşısındaki kenara hipotenüs denir. Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

Kenarlarının uzunlukları x cm ve 3x cm olan dikdörtgen şeklindeki karton ile bir yüzünün alanı 80 cm2 olan kare şeklindeki kâğıt aşağıda verilmiştir.
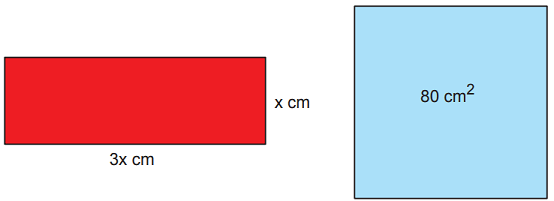
Bu karton ve kâğıt üst üste yerleştirildiğinde ikişer köşeleri aşağıdaki gibi çakışmaktadır.
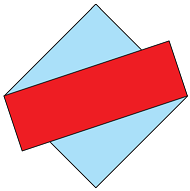
Buna göre dikdörtgen şeklindeki kartonun çevresinin uzunluğu kaç santimetredir?
Alanı 80 cm2 olan karenin kenar uzunluğu ... cm'dir. Bu karenin köşegen uzunluğunu bulabilmek için Pisagor bağıntısını kullanabiliriz.
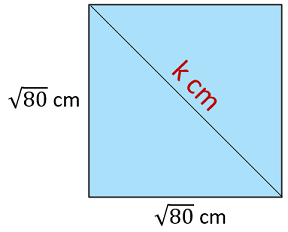
... ... ... cm2
⇒ ... cm
Bu uzunluk aynı zamanda kırmızı dikdörtgene ait köşegenin de uzunluğudur. Bu bilgiyi ve Pisagor bağıntısını kullanarak x'in değerini elde edebiliriz.
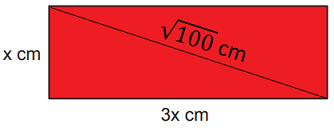
...
⇒ ...
⇒ ...
⇒ ...
⇒ ...
Buna göre, kırmızı dikdörtgenin çevre uzunluğu
... ... ... ... cm'dir.
CEVAP: A
Kare şeklindeki bir kâğıdın bir yüzü aşağıdaki gibi sekiz eş beyaz bölgeye ve dört eş mavi bölgeye ayrılmıştır.

Beyaz bölgelerden her biri, alanı (4x2 + 8x + 4) cm2 olan karesel bölgelerdir.
Buna göre mavi bölgelerden birinin alanını santimetrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
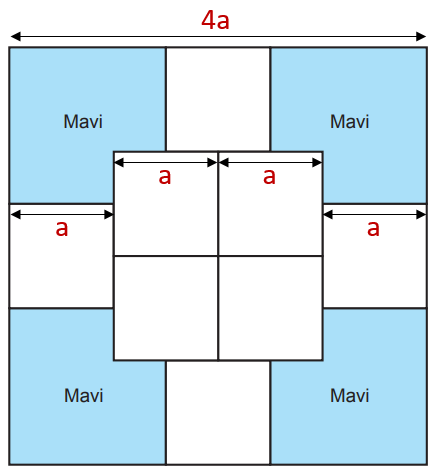
Santimetre cinsinden beyaz kenar uzunluğuna a dersek kare şeklindeki kâğıdın kenar uzunluğu 4a cm ve alanı (4a)2 = 16a2 cm2 olur. Kâğıttaki beyaz karelerden her birinin alanı a2 cm2'ye eşit olduğundan bu karelerin kapladığı toplam alan 8a2 cm2'dir. Geriye kalan 16a2 – 8a2 = 8a2 cm2'lik kısım ise mavi bölgeye aittir.
Kâğıtta toplam 4 eş mavi bölge olduğundan bu bölgelerden her birinin alanı 8a2 ÷ 4 = 2a2 cm2'dir.Kısacası, bir mavi bölgenin alanı, beyaz karenin alanının 2 katıdır. Beyaz bölgelerden birinin alanı
a2 = 4x2 + 8x + 4 = 4(x2 + 2x + 1) = 4(x + 1)2
şeklinde ifade edilebildiği için mavi bölgelerden birinin alanını veren cebirsel ifade
2 . 4(x + 1)2 = 8(x + 1)2'dir.
CEVAP: B
... ve ..., ... tam sayılar olmak üzere
... ve ... dir.

Aşağıda kenarlarının uzunlukları 25 mm ve 84 mm olan dikdörtgen şeklinde bir karton verilmiştir.

Bu karton, kenarlarının uzunluğu 25 mm olan kare şeklindeki eş parçalara aşağıdaki gibi ayrılarak sırasıyla sarı, kırmızı, mavi, yeşil ve turuncu renklere boyanıyor. Her bir kare şekildeki gibi kesilerek boş bir torbaya atılıyor.

Bu torbadan rasgele çekilen bir karenin kırmızı kare olma olasılığı kaçtır?
Kare şeklindeki parçalardan her birinin genişliği 25 mm'dir. Kesilen parça sayısını bulabilmek için kartonun genişliğini parçalardan birinin genişliğine bölebiliriz.
... ... ... ...
Bu parçalar, beşerli gruplar halinde soruda belirtilen renklere boyanmıştır. İlk 125 parçada her renkten 125 ÷ 5 = 25 kare vardır. Son 3 parçadan ilki sarı, ikincisi kırmızı ve üçüncüsü mavidir. Buna göre, toplam 26 sarı, 26 kırmızı, 26 mavi, 25 yeşil ve 25 turuncu parça vardır. Rasgele seçilen bir parçanın kırmızı olma olasılığı, kırmızı parça sayısının tüm parçaların sayısına oranlanmasıyla bulunabilir.
...
CEVAP: C
Dik üçgenlerde, 90⁰ lik açının karşısındaki kenara hipotenüs denir. Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.


Eşkenar üçgen şeklindeki beş karton, dikdörtgen şeklindeki panonun ön yüzüne, birer kenarları ve birer köşeleri çakıştırılarak panonun yüzünden taşmayacak biçimde yukarıdaki gibi yerleştirilmiştir. Birer kenarları aynı doğru parçası üzerinde ve birer köşeleri ortak olan eşkenar üçgenlerin benzerlik oranı ... dir.
Bu üçgenlerden birinin çevresinin uzunluğu 96 cm olduğuna göre panonun ön yüzünün alanı en az kaç santimetrekaredir?
Çözümü daha iyi takip edebilmek için eşkenar üçgenleri isimlendirelim.

Panonun
eşittir. Alanın en küçük değerini bulabilmek için çevresi 96 cm olan üçgenin A üçgeni olduğunu varsaymamız gerekir. Bu durumda A üçgeninin kenar uzunluğu 96 ÷ 3 = 32 cm'ye ve yüksekliği ... cm'ye eşit olur.
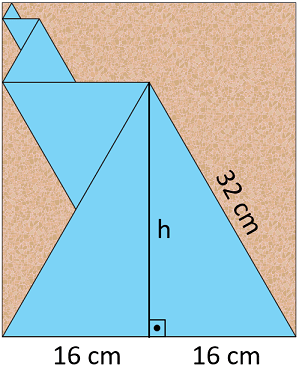
Üçgenler arasındaki benzerlik oranı ... olduğundan
Panonun yüksekliği A, C ve E üçgenlerine ait yüksekliklerin toplamına eşittir.
... ... cm
Genişliği ... cm ve yüksekliği ... cm olan dikdörtgen şeklindeki panonun alanı ... cm2'dir.
...
CEVAP: A
Efe aşağıda verilen ABC üçgeninin açılarının ölçülerini esnemeyen bir ip yardımıyla sıralayacaktır.
Efe bu ipin bir ucunu;
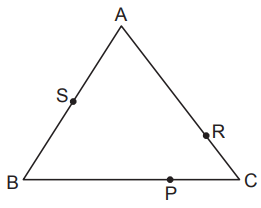
|BP| > |AS| > |CR| olduğuna göre ABC üçgeninin iç açılarının ölçülerinin doğru sıralanışı aşağıdakilerden hangisidir?
Efe'nin kullandığı ip
üzerini kaplamaktadır. İpin uzunluğu her bir durumda kapladığı doğru parçalarının uzunlukları toplamına eşittir. Bu uzunluğa x dersek,
Buna göre, üçgenin kenar uzunlukları x cinsinden aşağıdaki gibi yazılabilir.
x'ten ne kadar büyük bir sayı çıkarırsak, sonuç o kadar küçük olur. Dolayısıyla, |BP| > |AS| > |CR| eşitsizliğini kullanarak |AB| < |CA| < |BC| sonucunu çıkarabiliriz. Bir üçgende büyük açı büyük kenarın karşısında olduğundan ... > ... > ...'dir.
CEVAP: D
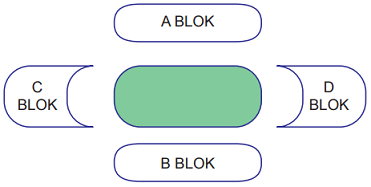
Yukarıda oturma planı verilen stadyumda oynanacak bir maç için satışa çıkarılan biletlerin %80'i satılmıştır. Biletlerin bloklara göre ücretlerini gösteren tablo ve satılmayan biletlerin sayısının bloklara göre dağılımını gösteren daire grafiği aşağıda verilmiştir.
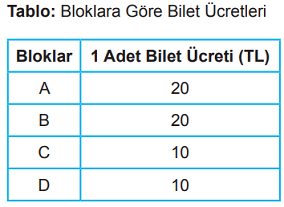

Satılmayan biletlerin toplam ücreti 15 000 TL olduğuna göre bu maç için satışa çıkarılan bilet sayısı kaçtır?
Satılmayan tüm biletlerin sayısına x dersek, daire grafiğini kullanarak farklı bloklardaki satılmayan bilet sayılarını x cinsinden aşağıdaki gibi bulabiliriz.
Bir bloktaki satılmayan biletlerin toplam ücretini bulabilmek için satılmayan bilet sayısı ile bir biletin ücretini çarparız.
Buna göre ... cinsinden satılmayan biletlerin toplam ücreti
... ... ...'dir.
Bu sayıyı 15 000'e eşitleyerek satılmayan bilet sayısını bulabiliriz.
...
⇒ ...
Tüm biletlerin %80'i satıldığına göre %20'si veya ...'i satılmamıştır. ...'i 1200 olan sayı 1200 . 5 = 6000'dir.
CEVAP: B
..., ..., ... birer doğal sayı olmak üzere
...
... ... dir.
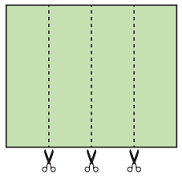
Dikdörtgen şeklindeki bir kâğıt, yukarıdaki gibi kesilerek dikdörtgen şeklinde dört eş parça elde edilmiştir. Bu parçaların kısa kenarları ile uzun kenarları çakıştırılarak aşağıdaki gibi iki farklı şekil oluşturulmuştur.
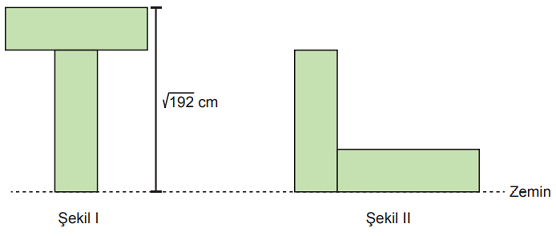
Şekil I'in yüksekliği ... cm ve Şekil II'nin çevresinin uzunluğu ... cm'dir.
Buna göre başlangıçta verilen dikdörtgen şeklindeki kâğıdın bir yüzünün alanı kaç santimetrekaredir?
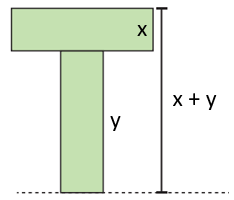
Parçaların kısa kenarına x ve uzun kenarına y dersek Şekil I'in yüksekliğini x + y şeklinde ifade edebiliriz. Bu uzunluk ... ... cm'ye eşittir.
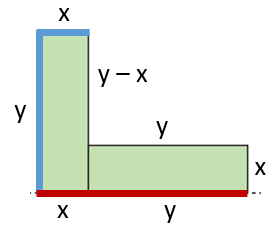
Şekil II üzerinde hem mavi hem de kırmızı ile işaretlediğimiz hatlardan her birinin uzunluğu x + y'ye ve dolayısıyla ... cm'ye eşittir.
Şekil II'nin çevre uzunluğundan bu iki hattın uzunluklarını çıkardığımızda geriye ... cm kalır.
... ...
Bu uzunluk y – x + y + x = 2y'ye eşittir. Buna göre ... cm ve ... ... cm'dir.
Dikdörtgen şeklindeki parçalardan birinin alanı kenar uzunluklarının çarpımına eşittir.
... ... cm2
Dolayısıyla, başlangıçtaki kağıdın bir yüzünün alanı 4 . 36 = 144 cm2'dir.
CEVAP: B
Eğim, dikey uzunluğun yatay uzunluğa oranıdır.
Dik üçgenlerde, 90⁰ lik açının karşısındaki kenara hipotenüs denir. Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

Bir parkın girişi için yapılacak kapı aşağıda modellenmiştir.

Kapının yapımı için her birinin uzunluğu 100 cm olan altı adet demir çubuk modeldeki gibi uç uca eklenecektir. Modelde verilen dikey doğru, genişliği 352 cm olan bu kapıyı iki eş parçaya bölmektedir. Modele göre 1. cubuk yere dik konumdadır ve 2. çubuğun eğimi %75'tir.
Buna göre 3. çubuğun eğimi kaçtır?
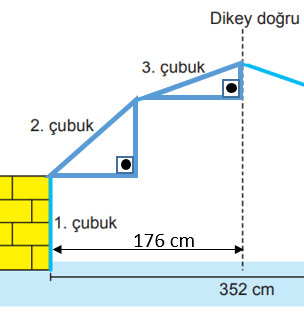
Hipotenüslerinde 2. ve 3. çubuklar olan tabanı yere paralel iki dik üçgen vardır. Bu üçgenlerin taban uzunluklarının toplamı kapının genişliğinin yarısına eşittir.
352 ÷ 2 = 176 cm
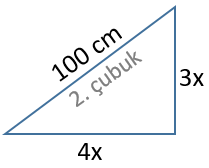
İkinci çubuğun eğimi %75 = ... olduğundan bu çubukla oluşturulan üçgenin yüksekliğini 3x ve taban uzunluğunu 4x ile gösterebiliriz. Bu durumda hipotenüsün uzunluğu 5x olur.
(3x)2 + (4x)2 = (5x)2
Hipotenüsün boyu 100 cm olduğu için x = 100 ÷ 5 = 20 cm'dir. Buna göre taban uzunluğu 4x = 80 cm'dir.
2. ve 3. çubukların oluşturduğu üçgenlere ait tabanların toplam uzunluğu 176 cm olduğundan 3. çubuğa ait üçgenin tabanı 176 – 80 = 96 cm uzunluğundadır.

Tabanı 96 cm ve hipotenüsü 100 cm olan dik üçgenin yüksekliği 28 cm'dir.
y2 + (96)2 = (100)2
⇒ y2 = 784
⇒ y = 28 cm
Buna göre, 3. çubuğun eğimi ...'e eşittir.
CEVAP: A
Bir elektronik eşya mağazasında 2019 ve 2020 yıllarında satılan K, L ve M marka televizyon sayılarının dağılımı, aşağıdaki daire grafiklerinde gösterilmiştir.

Bu mağazada 2020 yılında satılan L marka televizyon sayısı 2019 yılına göre 25 azalırken M marka televizyon sayısı 40 artmıştır.
Buna göre 2019 yılında satılan K marka televizyon sayısı kaçtır?
Daire grafiğinde 120⁰ ile gösterilen parça, bütünün ...'üne eşittir. Dolayısıyla, 2019 yılında satılan M marka televizyon sayısına x dersek, aynı yıl sayılan tüm televizyonların sayısı 3x olur. Yine 2019 yılında 90⁰ ile gösterilen L marka televizyonların sayısı, aynı yıl satılan tüm televizyonların sayısının ...'üne eşittir. Bu sayıyı ... şeklinde ifade edebiliriz.
Satılan M marka televizyonların sayısı 2020 yılında 25 azaldığına göre ikinci yıl için bu sayıyı ... şeklinde gösterebiliriz. Bu ifade sağdaki grafikte 90⁰ ile gösterildiği halde satılan M marka televizyonlar aynı grafikte 180⁰ ile gösterilmiştir. Buna göre, 2020 yılında satılan M marka televizyon sayısı ...'in 2 katıdır.
... ... (1)
Soruda verilenlere göre, 2020 yılında satılan M marka televizyon sayısı x'ten 40 fazladır. Dolayısıyla, (1)'deki ifadeyi x + 40'a eşitleyerek x'in değerini bulabiliriz.
... ...
⇒ ... ...
⇒ ...
⇒ ...
2019 yılında satılan M marka televizyon sayısı 180 ise, aynı yıl satılan televizyon sayısı 180 . 3 = 540'tır. Soldaki grafikte K marka televizyonlar 360⁰ – (120⁰ + 90⁰) = 150⁰ ile gösterilmiştir. Buna göre 2019 yılında satılan K marka televizyon sayısı
...'tir.
CEVAP: C