SÜRE
40:002022-2023 LGS MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8➤DENEME OLARAK ÇÖZ➤ 2022-2023 LGS
SÜRE
40:00
Aşağıdaki sorularMilli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.

1–5, (–3)2, 2–3, –32üslü ifadeleri yukarıdaki sayı doğrusunda, değerlerine karşılık gelen noktalara yerleştirilecektir.
Buna göre, hangi renkteki doğru parçası üzerineen fazlasayıda üslü ifade yerleştirilir?
Çözüm:
Verilen üslü ifadelerin değerlerini ve hangi alanlara yerleştirileceklerini bulalım.
Noktalardan ikisi
CEVAP: C
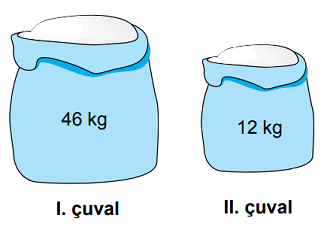
Yukarıda iki adet un çuvalı ve bu çuvallarda bulunan un miktarları verilmiştir. Bu çuvallara belli miktarlarda un eklendiğinde çuvallardaki un miktarlarının kilogram cinsinden değerleri, aralarında asal olmaktadır.
Buna göre, çuvallara eklenen un miktarlarının kilogram cinsinden değerleri aşağıdakilerden hangisi olabilir?
Seçeneklerde verilen miktarları çuvallara eklediğimizde, kilogram cinsinden yeni miktarlar aşağıdaki gibi olur.
| I. çuval | II. çuval | |
|---|---|---|
| 46 + 5 = 51 | 12 + 4 = 16 | |
| 46 + 8 = 54 | 12 + 6 = 18 | |
| 46 + 3 = 49 | 12 + 2 = 14 | |
| 46 + 9 = 55 | 12 + 3 = 15 |
kalansız bölünür.
A seçeneğindeki sayıların ortak çarpanı yoktur.51ile16sayıları aralarında asaldır.
CEVAP: A
...,...birer doğal sayı olmak üzere
...dir.
Yükseklikleri 5 m ve 6 m olan A ve B direkleri arasına, boyu 2 m olan bir fidan dikilmiştir.
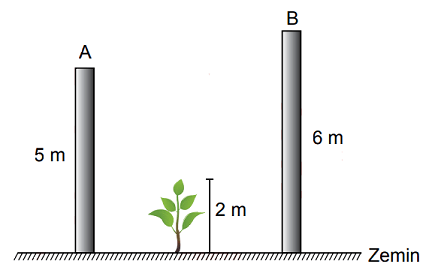
Bir süre sonra bu fidanın boyu A direğinin yüksekliğinden fazla, B direğinin yüksekliğinden az olmuştur.
Buna göre bu fidan, dikildikten sonra kaç metre uzamış olabilir?
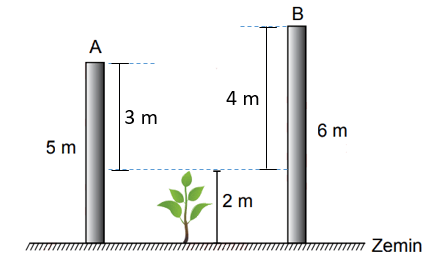
Bu fidanın boyu 3 m ile 4 m arasında uzamıştır.Seçeneklerde verilen kareköklü ifadelerin hangi tam sayılar arasında olduklarını bulalım.
8'e en yakın tam kare sayılar 22 = 4 ve 32 = 9'dur. Buna göre,...sayısı
12'ye en yakın tam kare sayılar 32 = 9 ve 42 = 16'dır. Dolayısıyla,...ifadesinin değeri
18'e en yakın tam kare sayılar 42 = 16 ve 52 = 25'tir. Bu nedenle,...ifadesi
24'e en yakın tam kare sayılar 42 = 16 ve 52 = 25'tir. Bu ifade de
CEVAP: B
...,...,...,...birer doğal sayı olmak üzere
...
...dir.
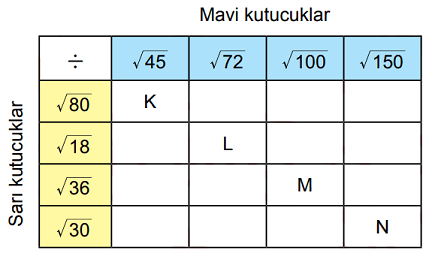
Yukarıdaki bölme işlemi tablosunda K, L, M ve N harflerine karşılık gelen sayılar, bu harflerle aynı sütunda bulunan mavi kutucuktaki kareköklü ifadenin bu harflerle aynı satırda bulunan sarı kutucuktaki kareköklü ifadeye bölünmesiyle elde edilmiştir.
Buna göre, bu harflerden hangisi bir irrasyonel sayı belirtmektedir?
Tüm sadeleştirmelere rağmen karekök içerisinde tam kare olmayan bir sayı elde ediyorsak, bölme işleminin sonucu irrasyoneldir.
CEVAP: D
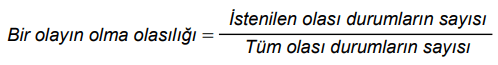
Aşağıda verilen abaküste üç basamaklı 423 sayısı modellenmiştir.
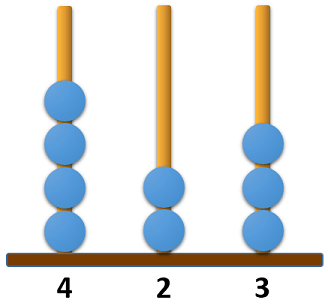
Bu abaküsteki boncuklardan bir tanesi, bulunduğu çubuktan çıkarılarak diğer çubuklardan birine takılıyor.
Buna göre, abaküste modellenen yeni sayının 500'den büyük olma olasılığı kaçtır?
6 farklı durumla karşılaşabiliriz.
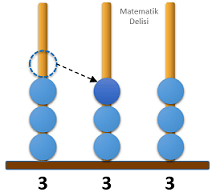
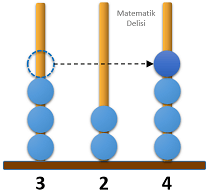
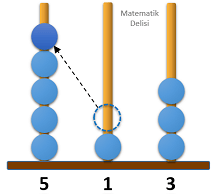
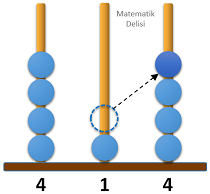
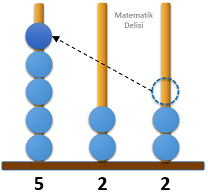
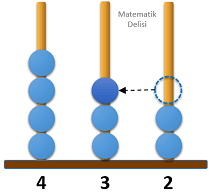
6 durumun 2'sinde 500'den büyük bir sayı elde ettiğimiz için yeni sayının 500'den büyük olma olasılığı...'tür.
CEVAP: B
...,...birer doğal sayı olmak üzere
...dir.
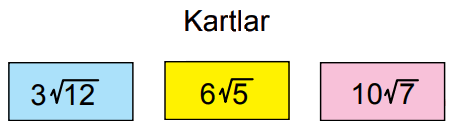
Yukarıdaki kartların ön yüzlerinde birer kareköklü ifade verilmiştir. Her bir kartın arka yüzünde ise ön yüzünde yazan kareköklü ifadenin...biçimindeki farklı bir gösterimi yazmaktadır.
Buna göre, aşağıdakilerden hangisi bu kartlardan herhangi birinin arka yüzünde yazılıolamaz?
Kartların ön yüzündeki ve seçeneklerdeki sayıları karekök içerisine alıp, karşımıza çıkan sayıları karşılaştırabiliriz.
Kartlardaki sayılar:
Seçeneklerdeki sayılar:
Buna göre,
C seçeneğindeki sayı bu kartlardan herhangi birinin arka yüzünde yazılı olamaz.
CEVAP: C
Efe ve Kuzey'in her ikisinin de bilye sayıları 50'den fazla ve birbirine eşittir. Efe, bilyelerinin tamamını her birinde eşit sayıda bilye olacak şekilde 3 torbaya; Kuzey ise bilyelerinin tamamını her birinde eşit sayıda bilye olacak şekilde 4 torbaya aşağıdaki gibi yerleştirmiştir.

Efe ve Kuzey, birer torba bilyelerini değiştiklerinde Kuzey'in toplam bilye sayısıen azkaç olur?
Efe'nin bilye sayısına x dersek, Kuzey'in bilye sayısı da x olur. x tane bilye hem 3 hem de 4 torbaya eşit olarak paylaştırılabildiğine göre, bu sayı hem 3 hem de 4'ün tam katıdır. 3 ve 4 sayılarının en küçük ortak katı (EKOK'u) 12'dir.
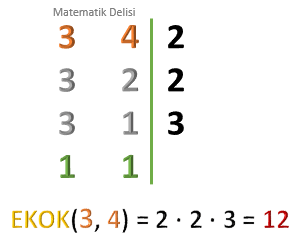
Bu sayıların diğer ortak katları, EKOK'un tam katlarıdır: 24, 36, 48, 60, 72...
50'den büyük olan ortak katlardan en küçüğü 60'tır.
60 bilye 3 torbaya eşit olarak paylaştırıldığında her torbada 60÷3 = 20 ve 4 torbaya eşit olarak paylaştırıldığında her torbada 60÷4 = 15 bilye olur. Buna göre, Efe'nin torbalarında 20'şer ve Kuzey'in torbalarında 15'er bilye vardır. Kuzey, 15 bilye verip karşılığında 20 bilye alırsa, başlangıçta 60 olan bilye sayısı 5 artar ve 60 + 5 = 65olur.
CEVAP: B
Dikdörtgen şeklindeki bir tarlanın kenarlarının uzunlukları Şekil I'de verilmiştir. Bu tarlanın iç bölgesine, üç kenarı boyunca kenarlara paralel olacak biçimde Şekil II'de gösterildiği gibi bir yol yapılacaktır.
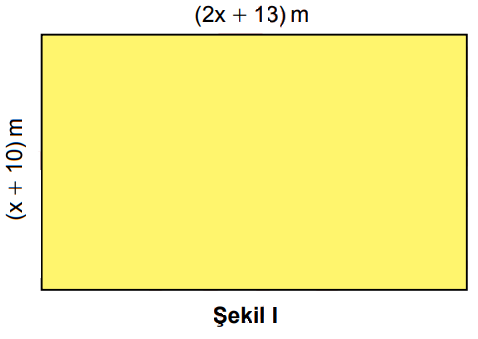
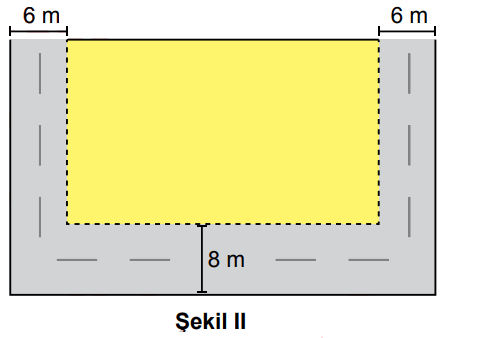
Buna göre, yol için ayrılan bölgenin alanını metrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
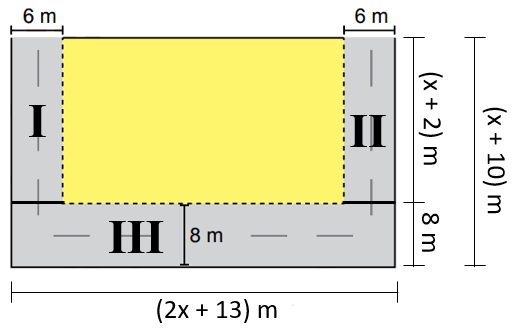
Yolu üç bölgeye ayırdığımızda
elde ederiz.
Bu alanların toplamı
(6x + 12) + (6x + 12) + (16x + 104) = 28x + 128 = 4(7x + 32) m'dir.
CEVAP: A
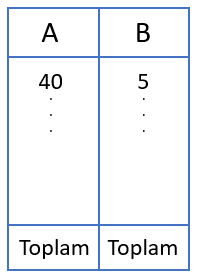
40 sayısının pozitif tam sayı çarpanlarının tamamı yukarıdaki gibi iki gruba ayrıldığında A grubundaki sayıların toplamı, B grubundaki sayıların toplamına eşit olmaktadır.
A grubundaki sayılardan biri 40 ve B grubundaki sayılardan biri 5 olduğuna göre, B grubundakien küçüksayı kaçtır?
40'ın pozitif tam sayı çarpanları 1, 2, 4, 5, 8, 10, 20 ve 40'tır. Bu çarpanların toplamı
1 + 2 + 4 + 5 + 8 + 10 + 20 + 40 = 90'dır.
A ve B grubundaki sayıların toplamları eşitse, bu toplamlardan her biri 90÷2 = 45'tir. Buna göre, A grubunda 40'ın dışında kalan sayıların toplamı 45 – 40 = 5 olmalıdır. Yalnız 5 sayısı B grubunda olduğundan, bu toplamı ancak 1 ve 4 sayılarıyla sağlayabiliriz. Dolayısıyla, 1, 4 ve 40 sayıları A grubunda, geriye kalan çarpanlar (2, 5, 8, 10 ve 20) ise B grubundadır.
Sonuç olarak, B grubundaki en küçük sayı2'dir.
CEVAP: B
Dört farklı markaya ait televizyonun TL cinsinden fiyatlarının asal çarpanlarının çarpımı şeklinde yazılışı aşağıda gösterilmiştir. Bu asal çarpanlardan küçük olanı a'dır.
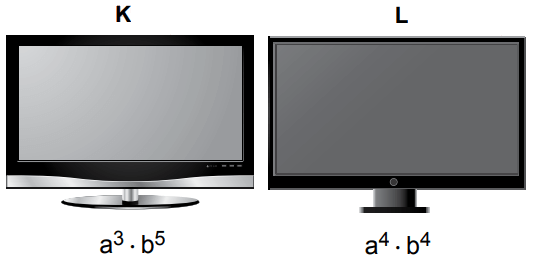
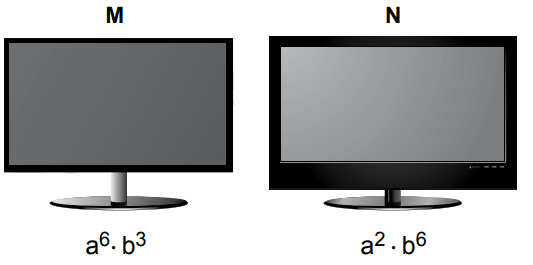
Bu televizyonlardan birinin fiyatı 10 000 TL olduğuna göre, televizyonlarınen ucuzuaşağıdakilerden hangisidir?
10 000 sayısının asal çarpanların çarpımı şeklinde yazılışı 24· 54'tür.
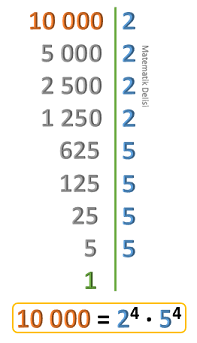
Görseldeki televizyonların altında yazan ifadelerin kuvvetlerine bakarak fiyatı 10 000 TL olan televizyonun L olduğunu görebiliriz.
24· 54 = a4· b4ve küçük asal çarpan a ise, a = 2 ve b = 5'tir. Bu sayıları kullanarak diğer televizyonların fiyatını bulalım.
Yukarıdaki sayıları karşılaştırdığımızda en ucuz televizyonunMolduğunu görebiliriz.
CEVAP: C
...,...,...birer doğal sayı olmak üzere
...
......
......dir.
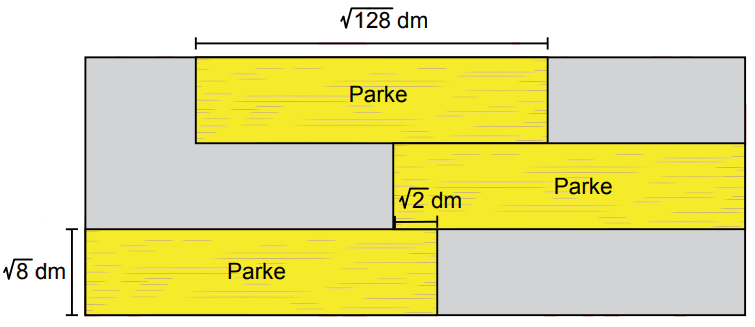
Yukarıda verilen dikdörtgen şeklindeki bir zemine parke döşenmektedir. Zeminde döşeli dikdörtgen biçiminde üç özdeş parke ile ilgili bazı ölçüler şekilde verilmiştir.
Buna göre, parkedöşenmemişbölgelerin alanları toplamı kaç desimetrekaredir?
Görseldeki parkenin taban ve yüksekliğini aşağıdaki gibi yazabiliriz.
Taban:......dm
Yükseklik:......dm
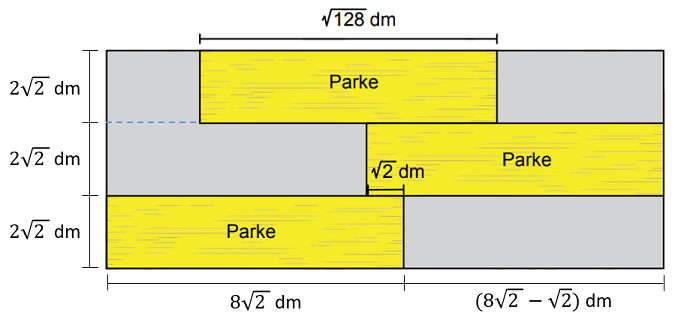
Zemini ifade eden dikdörtgenin yüksekliği 3 parkenin yüksekliklerinin toplamına eşittir.
......dm
Tabanı ise iki parkenin taban uzunlukları toplamından...dm azdır.
......dm
Buna göre zeminin toplam alanı
.........dm2'dir.
Her bir parkenin alanı
.........dm2
olduğundan 3 parkenin toplam alanı 3 × 32 = 96 dm2'dir. Dolayısıyla, zeminde parke döşenmemiş alanların toplamı
180 – 96 = 84 dm2'dir.
CEVAP: B
Bir müşterinin alışveriş yaptığı A ve B mağazalarında TL cinsinden ödeyeceği toplam tutarın dağılımı, daire grafiğinde; A mağazasında ödeyeceği toplam tutarın taksitleri, birim kareli zeminde verilen sütun grafiğinde gösterilmiştir.


Bu müşteri, B mağazasına 1800 TL ödemiştir.
Buna göre, bu müşterinin A mağazasına ödeyeceği 1. taksit kaç liradır?
Müşterinin B mağazasına ödediği 1800 TL, daire grafiğinde 120°'lik bir dilimle gösterilmiştir. Geriye kalan dilimin merkez açısı 360° – 120° = 240°'dir. 240°'lik açı 120°'nin 2 katı olduğu için müşterinin A mağazasına ödediği miktar 1800 × 2 = 3600 TL'dir.
Sütun grafiğinde, 1. taksit 3 birim, 2. taksit 4 birim ve 3. taksit 5 birim uzunluğunda sütunlarla gösterilmiştir. Buna göre ödenecek 3600 TL, toplam 3 + 4 + 5 = 12 birimle ifade edilmiştir. 1 birime karşılık 3600÷12 = 300 TL denk geldiği için 1. taksit 3 × 300 = 900 TL'dir.
CEVAP: D
Alanı (36x2) cm2olan kare, alanları birbirine eşit olan mavi, sarı ve beyaz renkli üç dikdörtgensel bölgeye aşağıdaki gibi ayrılmıştır.
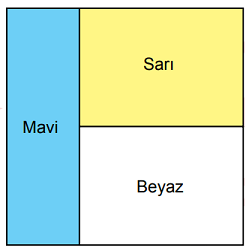
Buna göre, sarı dikdörtgensel bölgenin çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
36x2 = 6x · 6x olduğundan, karenin kenar uzunluğu 6x cm'dir. Mavi, sarı ve beyaz dikdörtgenlerin alanları eşit ve bu alanların toplamı (36x2) cm2'dir. Buna göre dikdörtgenlerden her birinin alanı (36x2)÷3 = (12x2) cm2'dir.
Verilen şekle göre, sarı ve beyaz dikdörtgenlerin genişlikleri eşittir. Alanları da eşit olan bu dikdörtgenlerin yükseklikleri de eşit olmalıdır. Bu yükseklik, karenin kenar uzunluğunun yarısıdır.
(6x)÷2 = (3x) cm
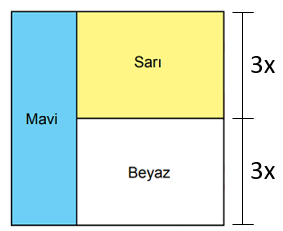
Alanı (12x2) cm2ve yüksekliği (3x) cm olan sarı dikdörtgenin genişliği (12x2)÷(3x) = (4x) cm'dir.
Genişliği (4x) cm ve yüksekliği (3x) cm olduğu için sarı dikdörtgenin çevresi 2(4x + 3x) = 14x cm'dir.
CEVAP: C
a ≠ 0, b ≠ 0 ve m, n tam sayılar olmak üzere
(an)m = an · mve an· am = an + mdir.
Bir buğday ekme makinesinin toprağa tohum bırakan 16 adet bölümü vardır.Her bir bölümdenher 15 saniyede 45adet buğday tanesi toprağa ekilmektedir. Bir buğday tanesinin kütlesi 2–5gramdır.
Buna göre, bu makine 60 dakikada kaç gram buğday ekmiştir?
Her bölümden her 15 saniyede bir 45 = (22)5 = 22 · 5 = 210buğday ekilmektedir. 1 dakika, 15 saniyenin 4 = 22katıdır. Buna göre, makinenin her bölümünden 1 dakikada 22· 210 = 22 + 10 = 212buğday tanesi ekilmektedir. 16 = 24bölümden ise toplam 24· 212 = 24 + 12 = 216buğday ekilmektedir.
60 dakikada ekilen buğday sayısı 60 · 216 = (15 · 4) · 216 = 15 · 22· 216 = 15 · 22 + 16 = 15 · 218'dir.
Ekilen buğday tanelerinin toplam kütlesi ise 15 · 218· 2–5 = 15 · 218 – 5 = 15 · 213gramdır.
CEVAP: A
...,...,...,...birer doğal sayı olmak üzere
......
......
......dir.
Her birinin çevresinin uzunluğu...cm olan eşkenar üçgen şeklindeki 6 adet sarı bayrak, köşeleri birbiriyle, kenarları ise iple çakışacak biçimde Şekil I'deki gibi bir ipe dizildiğinde ipin iki ucunda da boşluk kalmamıştır.
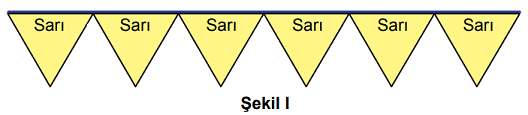
Aynı ipe, Şekil I'de verilen bayraklardan 4 tanesi ve eşkenar üçgen biçimindeki özdeş 3 mavi bayrak, köşeleri birbiriyle, kenarları ise iple çakışacak biçimde Şekil II'deki gibi dizildiğinde ipin her iki ucunda da boşluk kalmamıştır.
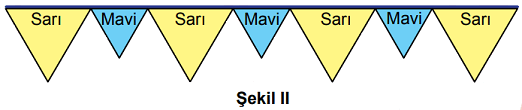
Buna göre, mavi bayraklardan birinin bir kenar uzunluğu kaç santimetredir?
Çevresi...cm olan sarı bayrağın kenar uzunluğu...cm'dir.
Üzerine 6 sarı üçgen sığan ipin uzunluğu ise...cm'dir.
İkinci şekilde, ipe 4 tane sarı üçgen asılmıştır. Sarı üçgenlerin ip üzerinde işgal ettiği kısmın toplam uzunluğu...cm'dir. Geriye kalan
......cm'lik
kısma 3 mavi üçgen asılmıştır. Buna göre, mavi üçgenlerin kenar uzunluğu...cm'dir.
CEVAP: D
Dikdörtgen biçimindeki bir kâğıt, Şekil I'deki gibi kesiliyor. Daha sonra elde edilen parçaların kenarları Şekil II'deki gibi çakıştırılarak bir yüzünün alanı (16x2) cm2olan, kare şeklinde bir kağıt elde ediliyor.

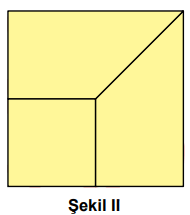
Buna göre, başlangıçta verilen dikdörtgen şeklindeki kâğıdın çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
16x2 = 4x · 4x olduğundan Şekil II'deki karenin kenar uzunluğu 4x cm'dir.

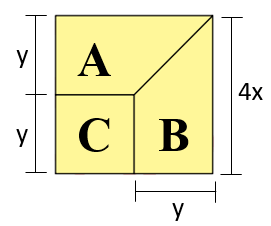
Şekil I'deki dikdörtgenin yüksekliğini y ile ifade edip, bu yüksekliği şekil II'de ilgili yerlere yazarsak C'nin bir kare olduğunu görebiliriz.
2y = 4x olduğundan y = 2x'tir. Buna göre, C karesinin kenar uzunluğu (2x) cm; A ve B yamuklarının kısa tabanları (2x) cm, uzun tabanları (4x) cm ve yükseklikleri (2x) cm uzunluğundadır.


Bulduğumuz uzunlukları yerlerine yazarak şekil I'deki dikdörtgenin çevresinin(20x) cmolduğunu görebiliriz.
4x + 2x + 2x + 2x + 2x + 4x + 2x + 2x = 20x cm
CEVAP: B
Dokuz eş kareden oluşan kare, Şekil I'de; dört eş dikdörtgenden oluşan dikdörtgen, Şekil II'de verilmiştir. Bu şekillerin yükseklikleri birbirine eşittir.
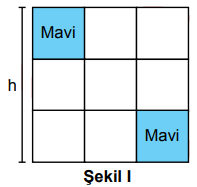
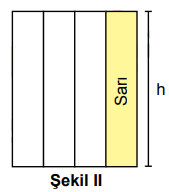
Şekil I'de verilen mavi bölgelerin alanları toplamı, Şekil II'de verilen sarı bölgenin alanına eşittir.
Şekil I'in çevresinin uzunluğu (36x + 36) cm olduğuna göre, Şekil II'nin çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Mavi karenin kenar uzunluğu, h yüksekliğinin 3'te 1'idir.
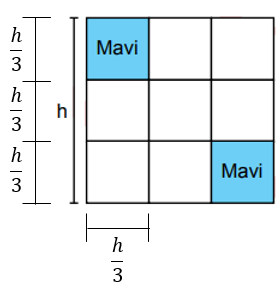
Alanı ise, bu uzunluğun karesidir.
Mavi karenin alanı = ...
İki mavi karenin toplam alanını bulabilmek için yukarıdaki ifadeyi 2'yle çarparız.
Mavi karelerin toplam alanı = ...
Sarı bölgenin tabanına y dersek, alanı y · h olur. Bu değer, mavi karelerin toplam alanına eşittir.
...
⇒...
Buna göre, sarı bölgenin tabanı...'dur.
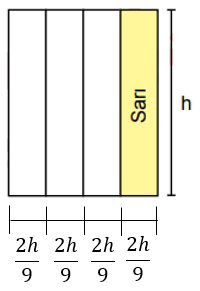
II. şeklin taban uzunluğu
...'dur.
Çevre uzunluğunu h cinsinden aşağıdaki gibi hesaplayabiliriz.
Çevre = ...
h uzunluğu, ilk şeklin çevresinin 4'te 1'idir.
......
Çevre için bulduğumuz...ifadesinde...yerine...yazarak sonuca ulaşabiliriz.
Çevre = ......
CEVAP: A
Bir markette başlangıçtaeşit kütlelerdekekik, nane, kimyon ve karabiber vardır. Bu ürünlerin belli miktarları satıldıktan sonra kalan kütlelerini gösteren tablo aşağıda verilmiştir.
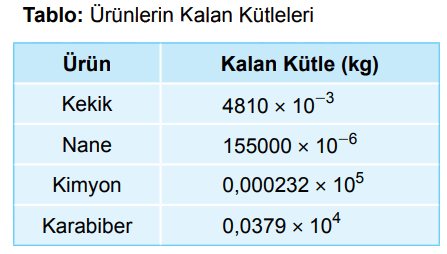
Buna göre, başlangıçta bu ürünlerden birinin kilogram cinsinden kütlesi aşağıdakilerden hangisi olabilir?
a bir tam sayı olmak üzere, bir sayıyı 10aile çarpmak,
anlamına gelir.
Verilen ürünlerden kalan kütlelerin kilogram cinsinden değerlerini bulalım.
Yukarıdaki sayılar satıştan geriye kalanları gösterdiği için bu ürünlerden her birinin başlangıçtaki kütlesi yukarıdaki sayılardan yüksek olmalıdır. Seçeneklerde verilen kütlelerin değerlerini bulup, 379'dan yüksek olanı işaretleyebiliriz.
D seçeneğindeki sayı 379'dan büyüktür.
CEVAP: D
Elektrikli otomobil üreten bir firma, bu otomobilllerin tercih edilme nedenlerini araştıran bir anket uygulanmıştır. Ankete katılan müşterilerin cinsiyetlerine ve verdikleri cevaplara göre dağılımları aşağıdaki daire grafiklerinde gösterilmiştir.


Anket sonuçlarına göre,
Ankete katılan her bir müşteri, grafikte gösterilen tercih edilme nedenlerinden yalnızca birini seçebildiğine göre, bu ankete katılanların toplam sayısı kaçtır?
Her müşteri yalnız bir nedeni seçebildiğine göre soldaki daire grafiğinin gösterdiği kişi sayısı, sağdaki daire grafiğinin gösterdiği cevap sayısına eşittir. Buna göre, aynı merkez açıya sahip olan dilimler iki grafikte de aynı sayıda kişiyi ifade etmektedir. Sol grafiktedki kadınlar 160° ile gösterildiğinden sağ taraftaki kadınların verdiği cevaplar da toplam 160° ile gösterilmelidir.
Şimdi soruda verilen anket sonuçlarına göre çıkarımlar yapalım.
"Ekonomikliği tercih eden erkeklerin sayısı, ekonomikliği tercih eden kadınların sayısının 3 katıdır."
Dolayısıyla, sağdaki grafikte 160° ile gösterilen dilimi seçen kadınlar 1 birim ise, aynı dilimi seçen erkekler 3 birimdir. Toplam 1 + 3 = 4 birim ile gösterilen 160°'lik merkez açıya sahip olan sarı dilimin 4'te 1'i (160°÷4 = 40°'si) kadınlardır.
"Sağlamlığı tercih eden erkeklerin sayısı, sağlamlığı tercih eden kadınların sayısına eşittir."
Sağlamlık kısmını gösteren dilimin merkez açısı
360° – (160° + 80°) = 120°'dir.
Bu dilimin yarısı erkek, yarısı kadın olduğundan kadınları temsil eden kısmın açısı 120°÷2 = 60°'dir.
"Konforu tercih eden kadınların sayısı 60'tır."
Soldaki grafiğin 160°'lik kısmını kadınlar oluşturmaktadır. Sağdaki grafikte ise sarı dilimin 40°'si, yeşil dilimin 60°'si ve mavi dilimin bir kısmı kadındır. İki grafikte de toplam açıların eşit olması gerektiğinden, kadınlar mavi dilimin
160° – (40° + 60°) = 60°'lik
kısmı ile ifade edilmelidir. 60°'lik kısım 60 kişiye karşılık geliyorsa tüm katılımcıları gösteren 360°'lik kısım360 kişiyekarşılık gelir.
CEVAP: C
Renkleri dışında özdeş olan yeterli sayıda top vardır. Bu toplar, her bir kutuda eşit sayıda top olacak şekilde başlangıçta boş olan I, II, III ve IV numaralı kutulara yerleştiriliyor.
Kutulardaki toplar, boş olan A, B, C torbalarında tablodaki gibi birleştirilirse bu torbalardan rasgele çekilen birer topun mavi olma olasılıkları tablodaki gibi olmaktadır.

Buna göre, başlangıçtaki bu dört kutuda bulunan mavi top sayısı aşağıdakilerden hangisi olabilir.
I. ve II. kutular birleştirildiğinde rasgele çekilen bir topun mavi çıkma olasılığı %100 ise hem I. hem de II. kutudaki topların tümü mavidir.
Verilen tabloya göre, I ve III. kutuların birleşiminden çekilen rasgele bir topun mavi olma olasılığı ise %75'tir. Olasılığın %75 = ...olması, bu iki kutunun birleşiminde her 4 toptan 3'ünün mavi olduğunu gösterir. Bu topların yarısı I. ve diğer yarısı III. kutudadır. Her 4 toptan 2'si I. kutudan gelen mavi toplar olduğundan, geriye kalan 2 toptan yalnız 1'i mavidir. Bu toplar III. kutudan geldiğine göre, bu kutudaki her 2 toptan 1'i mavidir.
I. ve IV. kutuların birleşiminden çekilen rasgele bir topun mavi olma olasılığı %50'dir. Olasılığın %50 olması bu birleşimdeki topların yarısının mavi olduğunu gösterir. Bu topların yarısının I. kutudan geldiği ve I. kutudaki tüm topların mavi olduğu göz önünde bulundurulduğunda IV. kutuda hiç mavi top olmadığı sonucu çıkarılabilir.
Özetle,
III. kutudaki mavi top sayısına 1 birim dersek, I. ve II. kutularda 2'şer birim mavi top vardır. Buna göre, kutulardaki toplam mavi top sayısı 2 + 2 + 1 = 5 birimdir. Mavi top sayısının 5 birim olması, bu sayının5'in tam katlarından biriolduğu anlamına gelir. Sadece A seçeneğindeki15sayısı, 5'in tam katıdır.
CEVAP: A