SÜRE
15:00DENKLEMLER
ÇÖZÜMLÜ KONU TESTİ

SÜRE
15:00
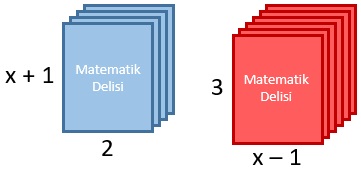
Esin, bir kırtasiyeden kenar uzunlukları 2 ve x + 1 birim olan mavi el işi kâğıtlarından 4 tane ve kenar uzunlukları 3 ve x – 1 birim olan kırmızı el işi kâğıtlarından 6 tane satın almıştır. Kartondan yaptığı küp şeklindeki bir cismin 4 yüzünü kırmızı ve 2 yüzünü mavi el işi kâğıtlarıyla kaplamıştır.
Bu işlem sonucunda hiç el işi kâğıdı artmadığına ve küpün yüzeyi tek kat el işi kâğıdıyla tamamen kaplandığına göre, x aşağıdakilerden hangisine eşittir?
Küp üzerinde, kırmızı kâğıtların kapladığı alan, mavi kâğıtların kapladığı alanın 2 katıdır.
2(8x + 8) = 18x – 18
⇒ 16x + 16 = 18x – 18
⇒ 16x + 16 + 18 = 18x
⇒ 16x + 34 = 18x
⇒ 34 = 18x – 16x
⇒ 34 = 2x
⇒ x = 17
CEVAP: C
Bir alışveriş merkezi, yan tarafındaki boş araziyi otopark yapmak için kiralamıştır.
Bu araziye, arabaların park etmesi için eşit boyutlarda dikdörtgenler çizilecektir. Araziye 10 dikdörtgen çizildiğinde geriye 80 metrekare, 15 dikdörtgen çizildiğinde 20 metrekare boş alan kalmaktadır.
Buna göre, alışveriş merkezinin kiraladığı arazi kaç metrekaredir?
Çizilen dikdörtgenlerden her birinin alanı x olsun.
Soruda verilenlere göre, kiralanan arazinin alanı hem 10x + 80'e hem de 15x + 20'ye eşittir. Bu iki ifadeyi birbirine eşitleyerek dikdörtgenin alanını bulabiliriz.
10x + 80 = 15x + 20
⇒ 80 = 15x + 20 – 10x
⇒ 80 = 5x + 20
⇒ 80 – 20 = 5x
⇒ 60 = 5x
⇒ x = 12
x = 12 ise kiralanan arazinin alanı 10x + 80 = 10 . 12 + 80 = 200 metrekaredir.
CEVAP: D


ABC bir üçgen ve KLMN bir dikdörtgendir. |BD| = x, |DC| = 1, |AD| = 3, |KN| = 2 ve |NM| = x – 1 birimdir.
ABC üçgeni ile KLMN dikdörtgeninin alanları eşitse, ADB üçgeninin alanı kaç birimkaredir?
Bu iki şeklin alanı için bulduğumuz ifadeleri eşitleyerek ... 'in değerini bulabiliriz.
... ...
⇒ ... ...
⇒ ... ...
⇒ ... ...
⇒ ... ...
⇒ ... ...
⇒ ...
... ifadesinde ... yerine ... koyarak ADB üçgeninin alanını bulabiliriz.
...
CEVAP: D

Yukarıda bir dikdörtgenler prizmasının ayrıt uzunlukları metre cinsinden verilmiştir.
Bu dikdörtgenler prizmasının metrekare cinsinden yüzey alanı, metreküp cinsinden hacmine eşitse, en büyük yüzünün alanı kaç metrekaredir?
Bu iki ifadeyi eşitleyerek x'in değerini bulabiliriz.
20x + 20 = 18x + 58
⇒ 20x = 18x + 58 – 20
⇒ 20x = 18x + 38
⇒ 20x – 18x = 38
⇒ 2x = 38
⇒ x = 19
Buna göre dikdörtgenler prizmasının yüzlerinin alanları
En büyük yüzün alanı 100 metrekaredir.
CEVAP: D

Bir kenarı x + 1 ve diğer kenarı 2x + 1 birim olan 6 dikdörtgen yukarıdaki gibi birleştirildiğinde bir kare oluşturuyorsa, bu dikdörtgenin alanı kaç birimkaredir?
Bir karenin kenar uzunlukları eşittir. Soruda verilen karenin yüksekliği 3(x + 1) = 3x + 3 ve tabanı 2(2x + 1) = 4x + 2 birimdir. Bulduğumuz yükseklik ve taban uzunluğunu birbirine eşitleyerek x'in değerini bulabiliriz.
3x + 3 = 4x + 2
⇒ 3x + 3 – 2 = 4x
⇒ 3x + 1 = 4x
⇒ 1 = 4x – 3x
⇒ x = 1
Buna göre dikdörtgenin kenar uzunlukları x + 1 = 1 + 1 = 2 ve 2x + 1 = 2 . 1 + 1 = 3 birim ve alanı 2 . 3 = 6 birimkaredir.
CEVAP: B

ax – a = 4 denklemindeki a'nın değeri, içerisinde 0'dan büyük tek basamaklı sayılar olan bir torbadan rasgele çekilen bir sayıya eşittir.
Buna göre ax – a = 4 denkleminin çözümünün tam sayı olma olasılığı aşağıdakilerden hangisine eşittir?
a'nın diğer değerleri için x tam sayı olmaz. x, 9 sayıdan 3'ü için tam sayı olduğuna göre, aradığımız olasılık ... 'tür.
CEVAP: B
Kısa kenarı 5 birim olan 4 eş dikdörtgenin toplam alanı A birimkareye ve kenar uzunluğu 4 birim olan 5 eş karenin toplam alanı B birimkareye eşittir.
A + B = 280 birimkare olduğuna göre, dikdörtgenlerin uzun kenarı kaç birim uzunluğundadır?
Dikdörtgenin uzun kenarına x dersek, alanı 5x olur. Bu dikdörtgenlerden 4 tanesinin alanı 20x'tir.
Karelerden birinin alanı 16'dır. Bu karelerden 5'inin alanı ise 80'dir.
Toplam alan 20x + 80'dir. Alanı 280'e eşitleyerek x'in değerini bulabiliriz.
20x + 80 = 280
⇒ 20x = 280 – 80
⇒ 20x = 200
⇒ x = 10
CEVAP: B
Damla ile Sude'nin başlangıçta 100'er ₺ paraları vardır.
Aynı kalemlerden Damla 4 ve Sude 12 tane aldığında, Sude'nin geriye kalan parası, Damla'nın geriye kalan parasının yarısına eşit oluyorsa, kalemlerin tanesi kaç ₺'dir?
Kalemlerin tanesi x ₺ olsun.
Damla'nın kalan parası (100 – 4x) ₺ ve Sude'nin kalan parası (100 – 12x) ₺'dir. Damla'nın kalan parasının yarısını Sude'nin kalan parasına eşitleyerek x'in değerini bulabiliriz.
... ...
⇒ ... ...
⇒ ... ...
⇒ ... ...
⇒ ... ...
⇒ ... ...
⇒ ...
⇒ ...
CEVAP: C

Erdem, yukarıdaki 4 ifadeyi kâğıtlara yazıp bir torbanın içerisine atmıştır. Daha sonra torbadan rasgele çektiği iki ifadeyi birbirine eşitleyip, bir denklem oluşturmuştur.
Erdem'in elde ettiği denklemin çözümü en fazla kaç olabilir?
Bu çözümlerden en büyüğü 1'dir.
CEVAP: B
Teoman'ın sadece 5 ₺'lik ve Murat'ın sadece 10 ₺'lik kâğıt paraları vardır. Teoman'la Murat'ın paralarının sayıları eşittir.
Murat tanesi 2 ₺ olan kalemlerden 2 tane ve Teoman aynı kalemlerden 4 tane almıştır. Murat'ın kalan parası, Teoman'ın kalan parasının 3 katıdır.
Murat tüm parasıyla kalem almak isteseydi, kaç kalem alabilirdi?
Teoman'ın parası x ise, Murat'ın parası 2x'tir. Kalemleri aldıktan sonra Murat'ın kalan parası 2x – 4 ve Teoman'ın kalan parası x – 8'dir. Soruda verilenlere göre 2x – 4 ifadesi, x – 8'in 3 katıdır.
2x – 4 = 3(x – 8)
⇒ 2x – 4 = 3x – 24
⇒ 2x – 4 + 24 = 3x
⇒ 2x + 20 = 3x
⇒ 20 = 3x – 2x
⇒ x = 20
Buna göre Teoman'ın 20 ₺ ve Murat'ın 40 ₺ parası vardır. Murat, bu parayla 2 ₺'lik kalemlerden 20 tane alabilirdi.
CEVAP: C