SÜRE
15:00CEBİRSEL İFADELERLE İŞLEMLER
ÇÖZÜMLÜ KONU TESTİ

SÜRE
15:00
Yarıçapı a olan bir dairenin alanı πa2'ye eşittir.

Yukarıdaki şekilde O1 merkezli dairenin yarıçapı R ve O2 merkezli dairenin yarıçapı r birimdir.
Buna göre, taralı alan aşağıdaki ifadelerden hangisine eşittir?
O1 merkezli dairenin alanı πR2'ye ve O2 merkezli dairenin alanı πr2'ye eşittir.
Taralı alan, bu iki dairenin alanları arasındaki farka eşittir.
Alan = πR2 – πr2 = π(R2 – r2)
Seçeneklerden hangisinde verilen ifadenin bu alana eşit olduğunu bulmamız gerekiyor.
C seçeneğindeki çarpma işlemini yaptığımızda sonucun alana eşit olduğunu görebiliriz.
π(R – r)(R + r)=π(R2 + Rr – rR – r2)
= π(R2 – r2)
CEVAP: C
Ayrıt uzunluğu a olan bir küpün hacmi a3'e eşittir.
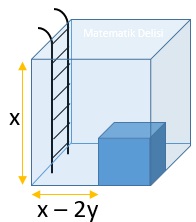
Ayrıt uzunluğu x birim olan küp şeklindeki bir havuzun tabanına havuz suyunun aktarılması ve arıtılması için kullanılan motorun ve filtrelerin yerleştirileceği, dış çeperi su geçirmeyen küp şeklinde bir odacık inşa edilmiştir.
Bu havuzun su kapasitesi aşağıdaki ifadelerden hangisine eşittir?
Odacık inşa edilmeden önce, havuzun hacmi x3 birimküptür.
İnşa edilen odacığın bir ayrıtı x – (x – 2y) = 2y birim ve hacmi (2y)3 = 8y3 birimküptür.
Buna göre, havuzun odacık inşa edildikten sonraki hacmi x3 – 8y3'tür.
Seçeneklerdeki işlemleri gerçekleştirerek, hangisinin x3 – 8y3'e eşit olduğunu bulabiliriz.
A) (x – 2y)(x2 + 2xy) + 4xy2 – 8y3
= x . x2 + x . 2xy – 2y . x2 – 2y . 2xy + 4xy2 – 8y3
= x3 + 2x2y – 2yx2 – 4xy2 + 4xy2 – 8y3
= x3 – 8y3
A seçeneğindeki işlem, aradığımız sonucu verdiği için diğer seçenekleri denememiz gerekmiyor.
CEVAP: A

ABCD bir dikdörtgen ve EBFD bir paralelkenardır.
|BC| = |CF|, |BF| = y... ve |AB| = x olduğuna göre EBFD paralelkenarının alanı hangisi ile ifade edilebilir?
Soruda verilenlere göre BCF ikizkenar dik üçgendir. Bu üçgenin hipotenüsü y... 'ye eşit olduğuna göre dik kenar uzunlukları y'ye eşittir.
Paralel kenarın tabanı x – y ve yüksekliği y olduğu için alanı y(x – y) = yx – y2 = – y2 + xy'dir.
CEVAP: C

Yukarıdaki tabloda 6 cebirsel ifade verilmiştir. Bu ifadelerden rasgele ikisi seçilerek çarpılacaktır.
Çarpım sonucu aşağıdakilerden hangisine eşit olamaz?
A) Turuncu ve yeşil dikdörtgenlerdeki ifadelerin çarpımı xy'dir.
B) Siyah ve sarı dikdörtgenlerdeki ifadelerin çarpımı (x – 1)(y – x) = xy – y – x2 + x'dir.
C) Kırmızı ve mavi dikdörtgenlerdeki ifadelerin çarpımı xy(x – y) = –xy2 + x2y'dir.
D) Tablodaki ifadelerden herhangi ikisini çarparak D seçeneğindeki ifadeyi elde edemeyiz.
CEVAP: D

x'in değeri tek basamaklı pozitif tam sayılar arasından rasgele seçilecektir.
Buna göre (x – 8)(x2 – 16) çarpımının pozitif olma olasılığı hangisine eşittir?
9 durumdan 4'ünde sonuç pozitif olduğu için aradığımız olasılık ... 'dur.
CEVAP: B

|AB| = x2 + 2x – 3xy, |BC| = 2x2 + 3x + xy ve |AC| = 2xy – 5x + x2 olduğuna göre ABC üçgeninin çevresi hangisine eşittir?
Üçgenin çevresini bulabilmek için verilen uzunlukları toplarız.
Çevre = |AB| + |BC| + |AC|
= x2 + 2x – 3xy + 2x2 + 3x + xy + 2xy – 5x + x2
= 4x2
CEVAP: C
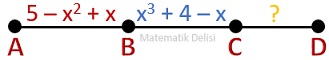
A, B, C ve D noktaları aynı doğru üzerindedir.
|AB| = 5 – x2 + x birim ve |BC| = x3 + 4 – x birimdir.
x'in değeri kaç olursa olsun A ve D noktaları arasındaki uzaklık 9 birime eşit çıkıyorsa, |CD| uzunluğu kaç birimdir?
x'in değerinden bağımsız olarak, |AB| + |BC| + |CD| toplamı 9'a eşittir.
|AB| + |BC| = 5 – x2 + x + x3 + 4 – x
= 9 – x2 + x3
Bu ifadeyle |CD|'nin toplamının 9'a eşit olabilmesi için |CD|'nin x2 – x3'e eşit olması gerekir.
CEVAP: B
Çap uzunluğu a olan bir dairenin çevresi πa'dır.
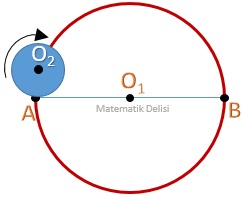
Yukarıdaki şekilde AB doğru parçası O1 merkezli dairenin merkezinden geçmektedir. O2 merkezli dairenin çapı (r2 + r) birimdir. Bu daire A noktasından başlayarak, AB doğru parçası üzerinde saat yönünde (r2 – 2r) tam tur attığında B noktasına ulaşmaktadır.
Buna göre, O1 merkezli dairenin çevresi kaç birimdir?
O2 merkezli dairenin çevresi π(r2 + r) birimdir. Bu daire (r2 – 2r) tur atarsa, toplam π(r2 + r)(r2 – 2r) birim yol alır. Bu işlemdeki parantezli ifadelerin çarpımı
(r2 + r)(r2 – 2r) = r2 . r2 + r2 . (–2r) + r . r2 + r . (–2r)
= r4 – r3 – 2r2'dir.
Buna göre, O1 merkezli dairenin çapı π(r4 – r3 – 2r2) ve çevresi
Çevre = π . π(r4 – r3 – 2r2)
= π2(r4 – r3 – 2r2)'dir.
CEVAP: A

Kenar uzunluklarından biri x birim olan dikdörtgen şeklindeki bir arazinin çevresi tamamen çitle kapatılacaktır.
Bu iş için gereken çitin uzunluğu 2y birimse, arazinin alanı kaç birimkaredir?
|AB| = |CD| uzunluğuna x diyelim. Bu dikdörtgenin çevresi 2y birimse, |BC| ve |DA| uzunlukları y – x birim olur. Buna göre, dikdörtgenin alanı
Alan = |AB| . |BC|
= x . (y – x)
= xy – x2
= –x2 + xy'dir.
CEVAP: C
Ayrıt uzunlukları a, b ve c olan bir dikdörtgenler prizmasının yüzey alanı 2ab + 2ac + 2bc'dir.

Dikdörtgenler prizması şeklindeki bir tuğlanın ayrıtları (x > y için) x, y ve x – y birimdir.
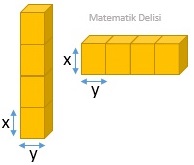
Bu tuğlaların yukarıda gösterildiği gibi üst üste ve yan yana konulmasıyla elde edilen dikdörtgenler prizmalarının yüzey alanları arasındaki fark aşağıdakilerden hangisi ile ifade edilebilir?
Birinci prizma:
Tuğlaların üst üste konulmasıyla elde edilen dikdörtgenler prizmasının ayrıtları 4x, y ve x – y birimdir. Buna göre yüzey alanı
Yüzey Alanı = 2. 4x . y + 2 . 4x . (x – y) + 2 . y . (x – y)
= 8xy + 8x(x – y) + 2y(x – y)
= 8xy + 8x2 – 8xy + 2yx – 2y2
= 8x2 + 2yx – 2y2'dir.
İkinci prizma:
Tuğlaların yan yana konulmasıyla elde edilen dikdörtgenler prizmasının ayrıtları x, 4y ve x – y birimdir. Buna göre yüzey alanı
Yüzey Alanı = 2 . x . 4y + 2 . x . (x – y) + 2 . 4y . (x – y)
= 8xy + 2x(x – y) + 8y(x – y)
= 8xy + 2x2 – 2xy + 8yx – 8y2
= 2x2 + 14yx – 8y2'dir.
Yüzey alanlar arasındaki fark:
Yüzey alanları arasındaki fark,
Fark = 8x2 + 2yx – 2y2 – (2x2 + 14yx – 8y2)
= 6x2 – 12xy + 6y2'dir.
A seçeneğinde verilen çarpma işleminin sonucu yüzeyler arasındaki farka eşittir.
6(x – y)2 = 6(x – y)(x – y)
= 6(x2 – 2xy + y2)
= 6x2 – 12xy + 6y2
CEVAP: A