SÜRE
15:00ÖZDEŞLİKLER
ÇÖZÜMLÜ KONU TESTİ

SÜRE
15:00
x – y, hangi seçenekteki taralı alanın çarpanlarından biri değildir?
A) Seçenekteki dikdörtgenin alanı (x + y)(x – y)'dir. x – y, bu ifadenin çarpanlarından biridir.
B) Taralı bölgenin alanı x2 – y2 = (x + y)(x – y)'dir. x – y, çarpanlardan biridir.
C) Taralı bölgenin alanı ... ... 'dir. x – y, bu ifadenin çarpanlarından biridir.
D) Seçenekteki üçgenin alanı ... 'dir. x – y, bu ifadenin çarpanlarından biri DEĞİLDİR.
CEVAP: D

Yukarıdaki şeklin alanı, aşağıdaki dik üçgenlerden hangisinin alanına eşittir?
Şekildeki üçgenin alanı ... ... 'dir.
Şimdi sırayla seçeneklerdeki üçgenlerin alanlarını bulalım.
A) Alan = ... ...
B) Alan = ...
C)Alan = ... ...
D) Alan = ... ...
A seçeneğindeki üçgenin alanı soruda verilen alanla aynıdır.
CEVAP: A
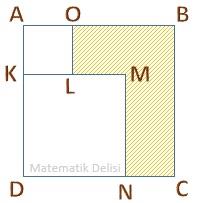
ABCD, AOLK ve KMND birer karedir.
|AO| = b ve |MN| = a ise taralı bölgenin alanı aşağıdakilerden hangisine eşittir?
AOLK karesinin alanı b2'dir.
KMND karesinin alanı a2'dir.
ABCD karesinin kenar uzunluğu
|AD| = |AK| + |KD| = |AO| + |MN| = b + a
ve alanı (a + b)2'dir.
Taralı bölgenin alanını bulabilmek için ABCD karesinin alanından AOLK ve KMND karelerinin alanlarını çıkarmamız gerekir.
Taralı Alan = (a + b)2 – a2 – b2
= a2 + 2ab + b2 – a2 – b2
= 2ab
CEVAP: A
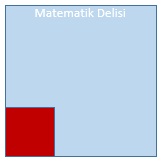
Yukarıda, kare şeklinde bir banyonun tabanı gösterilmiştir. Bu banyonun kırmızı ile gösterilen kısmına kare şeklinde bir duşakabin yerleştirilecektir. Tabanın geri kalan kısmına, kısa kenarı 1 dm ve uzun kenarı b – a dm olan fayanslardan döşenecektir. Banyo tabanının kenar uzunluğu b dm ve duşakabin için ayrılan bölümün kenar uzunluğu a dm'dir.
a ve b birer tam sayı ise taban döşemesi için en az kaç fayans gereklidir?
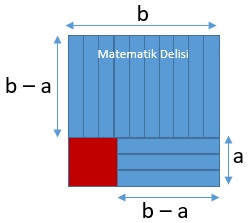
Banyonun taban alanı b . b = b2 dm2 ve duşakabin için ayrılan alan a . a = a2 dm2'dir. Buna göre, fayans döşenecek alan b2 – a2 = (b – a)(b + a) dm2'dir. Bu alanı bir fayansın alanına bölerek kaç fayans gerektiğini bulabiliriz. Bir fayansın alanı 1 . (b – a) = b – a dm2 olduğundan doğru cevap a + b'dir.
CEVAP: B
a, 1'den büyük pozitif bir tam sayı ise aşağıdakilerden hangisi a'nın 4. kuvvetinin 1 eksiğini kesinlikle kalansız böler?
a'nın 4. kuvvetinin 1 eksiği a4 – 1'dir. a4 = (a2)2 olduğu için
a4 – 1 = (a2 + 1)(a2 – 1)'dir.
Aynı özdeşliği ikinci çarpan için kullanırsak,
a4 – 1 = (a2 + 1)(a + 1)(a – 1)
eşitliğini elde ederiz. Buna göre a + 1 (a'nın 1 fazlası) soruda verilen ifadeyi kalansız böler.
CEVAP: A
Kareleri toplamı 125 ve çarpımları 50 olan iki pozitif sayının toplamı, bu sayıların farkından ne kadar fazladır?
Sayıların Toplamı:
Bu sayılar a ve b olsun.
(a + b)2 = a2 + b2 + 2ab
özdeşliğini kullanarak
(a + b)2 = 125 + 2 . 50 = 225
sonucunu elde edebiliriz. Buna göre sayıların toplamı ... = 15'tir.
Sayıların Farkı:
(a – b)2 = a2 + b2 – 2ab
özdeşliğini kullanarak
(a – b)2 = 125 – 2 . 50 = 25
sonucuna ulaşırız. Buna göre sayılar arasındaki fark ... = 5'e eşittir.
Sonuç:
Sayıların toplamı, farkından 15 – 5 = 10 fazladır.
CEVAP: A
a ve b pozitif tam sayılar olmak üzere, aşağıdaki ifadelerden en büyüğü hangisidir?
A, B ve C seçeneklerinin karşılaştırılması:
(a + b)2 = a2 + b2 + 2ab
a ve b pozitif tam sayılar olduğuna göre hem a2 + b2 hem de 2ab pozitiftir. İki pozitif sayının toplamı bu sayıların ikisinden de büyüktür. Buna göre (a + b)2, hem a2 + b2'den hem de 2ab'den büyük olmalıdır. (a + b)2, 2ab'den büyükse aynı zamanda ab'den de büyüktür. Kısacası, A seçeneğindeki ifade, B ve C seçeneklerindeki ifadelerden büyüktür.
A ve D seçeneklerinin karşılaştırılması:
Soruda b'nin pozitif tam sayı (1, 2, 3, ....) olduğu ifade edilmektedir. b = 1 için ab = a ve b > 1 için ab > a'dır. b'nin alabileceği hiçbir değer için a sayısı ab'den büyük olmadığı için 2ab'den küçüktür. Dolayısıyla, (a + b)2'den de küçüktür.
Yukarıdaki çıkarımlara göre, seçeneklerdeki en büyük ifade (a + b)2'dir.
CEVAP: A
Ceyda'nın dikdörtgen ve Uğur'un kare şeklinde bir arazisi vardır. Ceyda ve Uğur, bu arazilerin etrafını tamamen kapatmak için her biri n metre uzunluğundaki hazır çitlerden 4'er tane almışlardır. Bu çitler Uğur'un arazisine tam olarak uyduğu halde, Ceyda'nın arazisinin uzun kenarından 1 m kısa ve kısa kenarından 1 m uzundur.
Uğur'un arazisi x metrekare ise Ceyda'nın arazisi kaç metrekaredir?
Uğur'un arazisi n2 = x metrekare ise, Ceyda'nın arazisi n2 – 1 = x – 1 metrekaredir.
CEVAP: B
| CEBİRSEL İFADELER | ||
|---|---|---|
| x(x2y – y3) | ||
| xy(x – y)(x + y) | ||
| y(x3 – xy2) | ||
| x(x2 – xy)(x + y) | ||
Yukarıdaki tabloda verilen cebirsel ifadelerden rasgele biri seçilerek aşağıdaki eşitliğin sağ tarafına yazılacaktır.
x3y – xy3 = .....
Tablodaki ifadelerin seçilme olasılıkları eşitse oluşturulan eşitliğin bir özdeşlik olma olasılığı yüzde kaçtır?
Verilen 4 ifadeden 3'ü eşitliğin özdeşlik olmasını sağladığı için istenilen olasılık ... = %75'tir.
CEVAP: C

Bir zeytinyağı fabrikası, stoğundaki zeytinyağının tamamını n tenekeye eşit hacimlerle paylaştırıp, her birini n ₺'ye satmayı planlamıştır. Yalnız daha sonra, fabrika yöneticisi tenekelerdeki yağ miktarının az olduğunu düşünerek, 5 tenekedeki zeytinyağını geri kalanlara eşit şekilde paylaştırıp, satış fiyatına 5 ₺ zam yapmıştır. Boşalan 5 tenekeyi de hurdacıya satmayı planlamaktadır.
Önceki satış planı ile karşılaştırıldığında maddi zarara uğramaması için bu fabrikanın boşalan tenekelerin tanesini en az kaç ₺'ye satması gerekir?
1. Strateji:
n teneke zeytinyağının her biri n ₺'ye satılırsa, bu satıştan n . n = n2 ₺ elde edilir.
2. Strateji:
n – 5 teneke zeytinyağının her biri n + 5 ₺'ye satılırsa, bu satıştan (n – 5)(n + 5) = n2 – 25 ₺ elde edilir.
İki strateji arasındaki fark n2 – (n2 – 25) = 25 ₺'dir. Buna göre boş tenekelerden her birini en az ... = 5 ₺'ye satması gerekir.
CEVAP: B