SÜRE
15:00POZİTİF TAM SAYILARIN KUVVETLERİ
ÇÖZÜMLÜ KONU TESTİ

SÜRE
15:00
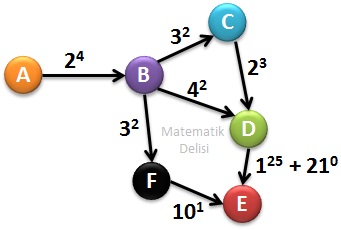
Yukarıdaki haritada A, B, C, D, E ve F şehirleri arasındaki yollar ve bu yolların kilometre cinsinden uzunlukları verilmiştir.
A şehrinden E şehrine yolculuk yapan biri en az kaç kilometre yol gitmelidir?
Önce üslü olarak verilen uzaklıkların değerlerini bulalım.
Yukarıdaki değerleri kullanarak, en kısa rotanın A → B → D → E olduğunu görebiliriz. Bu rotanın uzunluğu 16 + 16 + 2 = 34 km'dir.
Diğer alternatif rotaların uzunlukları aşağıdaki gibidir.
CEVAP: B
Aşağıdaki sayılardan basamak sayısı en fazla olan hangisidir?
A) 1125 = 1, tek basamaklıdır.
B) 10121 sayısında 1'in ardından 121 tane 0 gelir. Bu sayı 121 + 1 = 122 basamaklıdır.
C) 10060 sayısında 1'in ardından 2 × 60 = 120 tane 0 gelir. Bu sayı 120 + 1 = 121 basamaklıdır.
D) 100041 sayısında 1'in ardından 3 × 41 = 123 tane 0 gelir. Bu sayı 123 + 1 = 124 basamaklıdır.
CEVAP: D
21 – 75120 + 75131 + 07514 işleminin sonucu aşağıdakilerden hangisidir?
Öncelikle işlemde verilen üslü sayıların değerlerini bulalım.
Bu değerleri işlemde yerlerine yazdığımızda, sonucun 7514'e eşit olduğunu görebiliriz.
2 – 1 + 7513 + 0 = 7514
CEVAP: D
23 ile 24 arasında iki basamaklı kaç tek sayı vardır?
23 = 8 ve 24 = 16'dır. 8 ile 16 arasındaki iki basamaklı tek sayılar 11, 13 ve 15'tir.
CEVAP: A
2a = 64 ve 3b = 81 ise a + b aşağıdakilerden hangisine eşittir?
64'ü asal çarpanlarına ayırdığımızda
64 = 2 . 2 . 2 . 2 . 2 . 2 = 26
ve 81'i asal çarpanlarına ayırdığımızda
81 = 3 . 3 . 3 . 3 = 34
gösterimini elde ederiz. Buna göre a = 6 ve b = 4'tür. Soruda istenen toplam a + b = 6 + 4 = 10'dur.
CEVAP: C
75 + 75a = 76 ise a aşağıdakilerden hangisine eşittir?
75 + 75a = 76 ise 75a = 1 yapar. Bu üslü sayının 1'e eşit olabilmesi için a = 0 olmalıdır.
CEVAP: A
25 . a = 128 ise, a aşağıdakilerden hangisine eşittir?
25 = 2 . 2 . 2 . 2 . 2 = 32'dir. Eşitlikte 25 yerine 32 yazarsak,
32 . a = 128
⇒ a = 4
sonucunu elde ederiz.
CEVAP: C
a ve b doğal sayılar olmak üzere, 2a . b = 32 ise a + b’nin alabileceği en büyük değer aşağıdakilerden hangisidir?
32'yi
şeklinde gösterebiliriz.
a + b'nin alabileceği en büyük değer a'nın 0'a ve b'nin 32'ye eşit olduğu durumda elde edilir.
a = 0 ve b = 32 ise a + b = 32 olur.
CEVAP: C

Yukarıdaki harita, bir şehri kare şeklinde 1'er kilometrekarelik alanlara bölmektedir. Yapılan fiyat araştırmasına göre bu şehirde arazi fiyatlarını etkileyen tek faktör, içinde bulunduğu karenin konumudur. Kuzeye doğru 1 kare ilerledikçe, arazinin metrekare fiyatı 2 katına çıkmakta, doğu-batı doğrultusunda ise fiyat değişmemektedir.
A karesindeki arazilerin metrekare fiyatı 2 ₺ ise, B karesinden 120 metrekare arazi almak isteyen birinin kaç ₺ ödeme yapması gerekir?
A karesinden, B karesine ulaşmak için 4 birim kuzeye ilerlemek gerekir. Buna göre, B karesindeki arazilerin metrekare fiyatı 2 ₺ ile dört tane 2'nin çarpımıdır.
2 ₺ × 2 × 2 × 2 × 2 = 32 ₺
Metrekare fiyatı 32 ₺ olan 120 metrekare arazinin fiyatı 32 × 120 = 3840 ₺'dir.
CEVAP: C
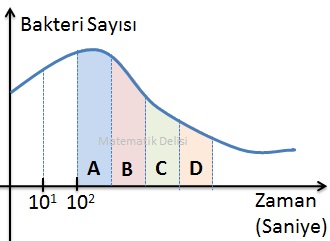
Yukarıdaki grafik, bir bakteri kolonisindeki bakteri sayısının zaman içerisindeki değişimini göstermektedir. Zaman ekseni logaritmik ölçekte çizildiği için bu eksendeki her nokta 1 birim solundaki noktanın 10 katı değere sahiptir.
102'nin sağında kalan ve zaman ekseninde birer birime karşılık gelen bölgeler, sırasıyla, A, B, C ve D harfleriyle gösterilmiştir.
Buna göre 9000. saniyedeki bakteri sayısını merak eden birinin bu grafikteki hangi bölgeyi incelemesi gerekir?
9000 sayısı 1000 ile 10 000 arasındadır. 1000 = 103 ve 10 000 = 104'tür. A ile B bölgelerinin sınır noktası 103'e; B ile C bölgelerini ayıran sınır noktası ise 104'e eşittir. Buna göre 9000. saniye, grafiğin B bölgesinde bulunmalıdır.
CEVAP: B