NEDEN?

3’e kalansız bölünebilme kuralını gösterirken, n basamaklı a_{n – 1}a_{n – 2}...a₁a₀ sayısının çözümlemesini yaptıktan sonra aşağıdaki eşitliği elde etmiştik.

a_{n – 1}a_{n – 2}...a₁a₀ = a_{n – 1}10^{n – 1} + a_{n – 2}10^{n – 2} + ... + a₁10¹ + a₀10⁰

= a_{n – 1}(10^{n – 1} – 1) + a_{n – 2}(10^{n – 2} – 1) + ... + a₁(10¹ – 1) + a_{n – 1} + a_{n – 2} + ... + a₁ + a₀

Ayrıca, bu eşitliğin sağındaki parantezli sayıların 3’e kalansız bölünebildiğini göstermiştik. Parantezli ifadelerin toplamına A ve parantezsiz ifadelerin toplamına B diyelim.

A = a_{n – 1}(10^{n – 1} – 1) + a_{n – 2}(10^{n – 2} – 1) + ... + a₁(10¹ – 1)

B = a_{n – 1} + a_{n – 2} + ... + a₁ + a₀

a_{n – 1}a_{n – 2}...a₁a₀ = A + B

A’nın çarpanlarından biri 3 olduğu için, p bir tam sayı olmak üzere, A sayısı 3p şeklinde yazılabilir. B’nin 3’e bölümünden kalan b ise, r bir tam sayı olmak üzere, B sayısı 3r + b şeklinde gösterilebilir. Buna göre A + B toplamı 3p + 3r + b’ye eşit olur. Bu toplamın 3’e bölümünden kalan b’dir.

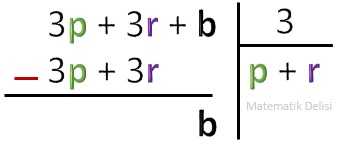
Özetle, a_{n – 1}a_{n – 2}...a₁a₀ sayısının 3’e bölümünden kalan, bu sayının basamakları toplamının 3’e bölümünden kalana eşittir.