BÖLÜM 2: SADELEŞTİRME

..., 1'den büyük bir doğal sayı olmak üzere, bir kesrin hem payının hem de paydasının ...'ya kalansız bölünebildiğini düşünelim. Bu kesrin payının ve paydasının ...’ya bölünmesine, ... ile sadeleştirme ismi verilir.
... kesrini 2 ile sadeleştirelim.

... kesrinin hem payı hem de paydası 2’ye kalansız bölünür. Bu kesri 2 ile sadeleştirebiliriz.
Payı 2’ye bölersek
... kesrini 5 ile sadeleştirelim.

Payı 5’e bölersek
Aşağıdaki boşlukları doldurun.
a) ... kesri, 2 ile sadeleştirildiğinde ...... olur.
b) ... kesri, 3 ile sadeleştirildiğinde ...... olur.
c) ... kesri, 4 ile sadeleştirildiğinde ...... olur.
ç) ... kesri, 7 ile sadeleştirildiğinde ...... olur.
d) ... kesri, 5 ile sadeleştirildiğinde ...... olur.
e) ... kesri, 11 ile sadeleştirildiğinde ...... olur.
SADELEŞTİRME VE DENK KESİRLER
![]() Bir kesir sadeleştirilmiş haline
denktir.
Bir kesir sadeleştirilmiş haline
denktir.
... kesrini sadeleştirerek, bu kesre denk bir kesir bulalım.
Hem pay hem de payda 3’e kalansız bölündüğünden, bu kesri 3 ile sadeleştirebiliriz. Payı 3’e böldüğümüzde 3 ÷ 3 = 1 sayısını ve paydayı 3’e böldüğümüzde 21 ÷ 3 = 7 sayısını elde ederiz. Buna göre, ... kesrini 3 ile sadeleştirdiğimizde, ... kesrine ulaşırız. Bu kesirler denk olduğu için aşağıdaki eşitliği yazabiliriz.
...
Sadeleştirme yaparak aşağıdaki kesirlere denk kesirler bulun.
a) ..., b) ..., c) ..., ç) ..., d) ...
NEDEN?

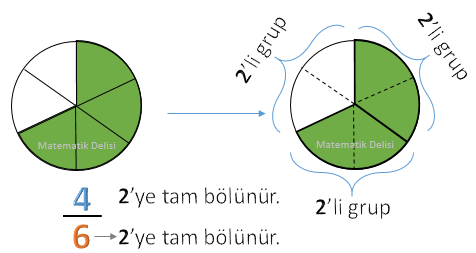
Eğer

Bu gruplardan her birini büyük parça olarak isimlendirdiğimizde, bütünü
SADELEŞTİRMENİN GÖSTERİMİ
![]() Sadeleştirme yaparken, genellikle, böldüğümüz sayının üzerini çizip sağ üstüne bölme işleminin sonucunu yazarız.
Sadeleştirme yaparken, genellikle, böldüğümüz sayının üzerini çizip sağ üstüne bölme işleminin sonucunu yazarız.
... kesrini sadeleştirelim.
| ... | Payı 2’ye bölersek 3 sonucunu elde ederiz. 6’nın üzerini çizip sağ üstüne 3 yazalım. |
| ... | Paydayı 2’ye bölersek 2 sonucunu elde ederiz. 4’ün üzerini çizip sağ üstüne 2 yazalım. |
| ... | Bulduğumuz sayılarla kesri tekrar yazalım. |
Yukarıda öğrendiğimiz gösterimi kullanarak, aşağıdaki kesirleri sadeleştirin.
a) ..., b) ..., c) ..., ç) ..., d) ..., e) ..., f) ..., g) ..., ğ) ..., h) ...
ART ARDA SADELEŞTİRMELER
![]() Bazı kesirlerde art arda birkaç sadeleştirme yapabiliriz.
Bazı kesirlerde art arda birkaç sadeleştirme yapabiliriz.
... kesrini önce 2 ve daha sonra 3 ile sadeleştirelim.
| ... | Pay: 6 ÷ 2 = 3 Payda: 12 ÷ 2 = 6 |
| ... | Pay: 3 ÷ 3 = 1 Payda: 6 ÷ 3 = 2 |
| ... | Sadeleştirme sonucunda kesrin payında 1 ve paydasında 2 kaldığını görüyoruz. |
...
... kesrini üç defa 2 ile sadeleştirelim.
| ... | Pay: 8 ÷ 2 = 4 Payda: 24 ÷ 2 = 12 |
| ... | Pay: 4 ÷ 2 = 2 Payda: 12 ÷ 2 = 6 |
| ... | Pay: 2 ÷ 2 = 1 Payda: 6 ÷ 2 = 3 |
| ... | Sonuç olarak, payında 1 ve paydasında 3 olan bir kesir elde ediyoruz. |
...
Aşağıdaki hesaplama aracını kullanarak yazdığınız kesirleri sadeleştirebilir ve tüm sadeleştirme basamaklarını inceleyebilirsiniz.
a) ... kesrini önce 2 ve daha sonra 5 ile sadeleştirin.
b) ... kesrini önce 2 ve daha sonra 3 ile sadeleştirin.
c) ... kesrini sırasıyla 2, 3 ve 2 ile sadeleştirin.
ç) ... kesrini üç defa 3 ile sadeleştirin.
d) ... kesrini önce 3 ve daha sonra 5 ile sadeleştirin.
SADELEŞTİRME SIRASI
![]() Sadeleştirme sırasını değiştirdiğimizde sonuç değişmez.
Sadeleştirme sırasını değiştirdiğimizde sonuç değişmez.
...’yi önce 2 ve daha sonra 3 ile sadeleştirdiğimizde ... denk kesrini elde etmiştik.
Şimdi aynı kesri önce 3 ve sonra 2 ile sadeleştirelim.
| ... | Pay: 6 ÷ 3 = 2 Payda: 12 ÷ 3 = 4 |
| ... | Pay: 2 ÷ 2 = 1 Payda: 4 ÷ 2 = 2 |
| ... | Sıralamayı değiştirdiğimiz halde, aynı sonucu elde ediyoruz. |
![]() Bir kesri art arda birkaç sayıyla sadeleştirmek yerine, tek seferde bu sayıların çarpımı ile de sadeleştirebiliriz.
Bir kesri art arda birkaç sayıyla sadeleştirmek yerine, tek seferde bu sayıların çarpımı ile de sadeleştirebiliriz.
... kesrini 2 ve 3 ile sadeleştirdiğimizde ... elde etmiştik.
Bunun yerine, bir defada 2 × 3 = 6 ile de sadeleştirme yapabiliriz.
| ... | Pay: 6 ÷ 6 = 1 Payda: 12 ÷ 6 = 2 |
| ... | Sonuçta yine aynı kesri elde ediyoruz. |
... kesrini üç defa 2 ile sadeleştirerek ... kesrini elde etmiştik.
Bunun yerine, direkt olarak 2 × 2 × 2 = 8 ile de sadeleştirme yapabiliriz.
| ... | Pay: 8 ÷ 8 = 1 Payda: 24 ÷ 8 = 3 |
| ... | Sonuçta yine ... kesrini elde ediyoruz. |
TAM SAYILI KESİRLERDE SADELEŞTİRME
![]() Tam sayılı bir kesir için, kesirli kısmı sadeleştirip, tam kısmında bir değişiklik yapmadan da denk bir kesir elde edebiliriz.
Tam sayılı bir kesir için, kesirli kısmı sadeleştirip, tam kısmında bir değişiklik yapmadan da denk bir kesir elde edebiliriz.
... kesrini 3 ile sadeleştirelim.
| ... | Pay: 6 ÷ 3 = 2 Payda: 15 ÷ 3 = 5 |
| ... | Tam kısmında bir değişiklik yapmıyoruz. |
...
ALIŞTIRMALARIN CEVAPLARI
a) ..., b) ..., c) ..., ç) ..., d) ..., e) ...
a) ..., b) ..., c) ..., ç) ..., d) ...
a) ..., b) ..., c) ..., ç) ..., d) ..., e) ..., f) ..., g) ..., ğ) ..., h) ...
a) ..., b) ..., c) ..., ç) ..., d) ...