BÖLÜM 1: İKİ BASAMAKLI SAYIYI TEK BASAMAKLI SAYIYA BÖLME

Bu konuda doğal sayıları nasıl bölebileceğimizi öğreniyoruz.

BÖLMENİN ÖĞELERİ

BÖLÜNEN: Böleceğimiz sayıya BÖLÜNEN ismini veririz. Bölüneni dikey çizginin sol üst tarafına yazarız.
BÖLEN: Bölüneni böldüğümüz sayıya BÖLEN deriz. Böleni yatay çizginin hemen üzerine yazarız.
BÖLÜM: Bölmeyi yaptıktan sonra bulduğumuz sonuca ise, BÖLÜM ismini veririz. İşlemi bitirdiğimizde, bölümü yatay çizginin hemen altında bulabiliriz.
KALAN: Bölme işlemi sonucunda artan doğal sayıya da KALAN adını veririz. Kalanı dikey çizginin solunda, en altta bulabiliriz. Bir bölme işleminde, bölünen, bölenin tam katı ise, kalan 0’a eşit olur. Tam katı olmadığı durumdaysa, kalan 0’dan büyük ve bölenden küçük bir doğal sayıdır.

BÖLME HESAPLAMA ARACI
👉🏻Aracı kullanmak için tıklayın👈🏻

İKİ BASAMAKLI SAYIYI TEK BASAMAKLI SAYIYA BÖLME

İlk olarak, kalanı sıfır olan bir bölme işlemini inceleyelim.

ÖRNEK:

38’i 2’ye bölelim.

	Bu işlemde bölünen 38 ve bölen 2'dir.
	Bölünenin en yüksek basamağı olan 3 ile başlayalım. Bu rakamı kullandığımızı unutmamak için üzerine kısa dik bir çizgi çekelim. Bölüme bir sayı yazabilmek için 3’ün içinde kaç tane 2 olduğunu bulalım. “3’ün içinde kaç tane 2 var?” ile “2’yi en fazla kaç ile çarparsak 3 veya 3’ten küçük olur?” sorularının yanıtları aynıdır. 2’yi en fazla 1 ile çarparsak, 3’ten küçük bir sayı elde edeceğimiz için işlemin bölüm kısmına 1 yazalım.
	Bölüme yazdığımız 1'i bölenle çarpıp, sonucu 3’ün altına yazalım. 1 × 2 = 2
	3’ten çarpma sonucunda bulduğumuz sayıyı çıkarıp, sonucu çizginin altına yazalım. 3 – 2 = 1
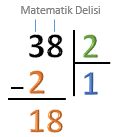
	Bölünenin bir sonraki basamağına geçelim. Bir sonraki rakam olan 8'in üzerine kısa bir çizgi çekip, çıkarma işleminde bulduğumuz 1'in yanına yazalım. Çıkarma çizgisinin altına yan yana yazdığımız 1 ve 8 sayılarını "18" olarak düşünelim.
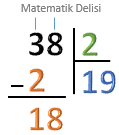
	İşleme devam edebilmek için “2’yi en fazla kaç ile çarptığımızda 18 veya 18’den küçük bir sayı elde ederiz?” sorusunun yanıtını bulmamız gerekir. 9 × 2 = 18 olduğu için aradığımız sayı 9’dur. Bölümde 1’in sağına 9 yazalım.
	9’u 2 ile çarpıp, sonucu 18’in altına yazalım. 9 × 2 = 18
	Çıkarma işlemi sonucunu alta yazalım. 18 – 18 = 0

Bölünende kullanacağımız rakam kalmadığı için bölme işlemini sonlandıralım.

Bu işlemde kalan 0 ve bölüm 19'dur.

2 BASAMAKLI SAYILARIN 1 BASAMAKLI SAYILARA BÖLÜMÜYLE İLGİLİ FAZLADAN 30 ÖRNEK İÇİN TIKLAYIN!

Şimdi de, kalanı sıfır olmayan bir bölme işlemi görelim.

ÖRNEK:

83’ü 3’e bölelim.

	Bu işlemde bölünen 83 ve bölen 3'tür.
	Bölünenin en yüksek basamağıyla başlayalım. 3’ü en fazla 2 ile çarparsak 8’den küçük bir sayı elde edeceğimiz için bölüme 2 yazalım.
	2 ile 3'ü çarpıp, sonucu 8'in altına yazalım. 2 × 3 = 6
	8’den 6’yı çıkaralım. 8 – 6 = 2
	Bölünenin bir sonraki rakamı 3'tür. Bu rakamı 2'nin sağına yazalım. 2 ile 3 yan yana geldiği için bu sayıyı 23 olarak düşünelim.
	3’ü en fazla 7 ile çarptığımızda 23’ten küçük bir sayı elde edeceğimiz için bölümdeki 2’nin yanına 7 yazalım.
	7 × 3 = 21 olduğu için 23’ün altına 21 yazıp, çıkarma işlemini yapalım.
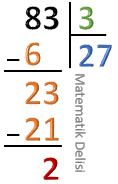
	23’ten 21’i çıkarınca 2 sayısını elde ederiz. 23 – 21 = 2

Bölünenin başka rakamı kalmadığı için bölme işlemini sonlandırabiliriz. Bu işlemde bölüm 27 ve kalan 2’dir.

2 BASAMAKLI SAYILARIN 1 BASAMAKLI SAYILARA BÖLÜMÜYLE İLGİLİ FAZLADAN 30 ÖRNEK İÇİN TIKLAYIN!

Bölünenin ilk rakamı bölenden küçük de olabilir. Bu durumda, bölenden daha büyük bir sayı elde edene kadar ilk rakamın yanına sırasıyla diğerlerini de ekler, böleceğimiz ilk sayının basamak sayısını artırırız.

ÖRNEK:

19’u 5’e bölelim.

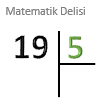
	Bu işlemde bölünen 19 ve bölen 5'tir.
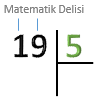
	Bölünenin en büyük basamağıdaki rakam olan 1’den başlayalım. 1, 5'ten küçük olduğu için bölünenin sonraki rakamını da kullanalım. 1’in yanına 9’u da ekleyelim.
	5’i en fazla 3 ile çarparsak 19 veya 19’dan küçük bir sayı elde ederiz.
	5 ile 3'ü çarpıp, sonucu 19'un altına yazalım. 5 × 3 = 15
	Çıkarma işlemini gerçekleştirelim. 19 – 15 = 4

Bölünende başka rakam kalmadığı için bölme işlemini sonlandıralım. Bu işlemde bölüm 3 ve kalan 4'tür.

2 BASAMAKLI SAYILARIN 1 BASAMAKLI SAYILARA BÖLÜMÜYLE İLGİLİ FAZLADAN 30 ÖRNEK İÇİN TIKLAYIN!

Çıkarma işleminin sonucunda elde ettiğimiz sayının yanına bölünenin yeni bir basamağını indirdiğimiz halde, hala bölenden küçük kalıyorsa, bölümün sağına bir tane 0 ekleriz.

ÖRNEK:

61’i 3’e bölelim.

	Bu işlemin bölüneni 61 ve böleni 3’tür.
	Bölünenin en büyük basamağındaki rakam olan 6 ile başlayalım. 3’ü en fazla 2 ile çarptığımızda 6 veya 6’dan küçük bir sayı elde edeceğimiz için bölüme 2 yazalım.
	2 × 3 = 6 olduğundan, bölünendeki 6’nın altına 6 yazalım.
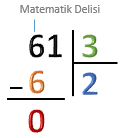
	Çıkarma işlemini yapalım. 6 – 6 = 0
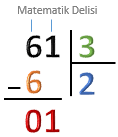
	Bölünenin birler basamağındaki 1’i çıkarma sonucunda elde ettiğimiz 0'ın sağına yazalım. Baştaki 0’ın bir önemi olmadığı için 01'i 1 olarak düşünelim.
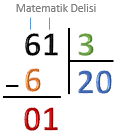
	1, 3’ten küçük olduğu için bölümdeki sayının sağına bir tane 0 ekleyelim.