BÖLÜM 1: DİKDÖRTGENİN ALANI
Bir kenarı 1 birim olan bir karenin alanı
1 birim2 (“bir birimkare”) olarak tanımlanır.
Alanın birimi, kenar uzunluklarının birimine göre değişir.
- Bir kenarı 1 cm olan bir karenin alanı 1 cm2 (“bir santimetrekare”) ve
- Bir kenarı 1 m olan bir karenin alanı 1 m2 (“bir metrekare”)’dir.
Alan, genellikle, A harfi ile gösterilir.
DİKDÖRTGENİN ALANI
Dikdörtgenin alanını aşağıdaki gibi farklı şekillerde ifade edebiliriz.
- Dikdörtgenin alanı, genişliği ile yüksekliğinin çarpımına eşittir.
- Dikdörtgenin alanı, komşu iki kenar uzunluğunun çarpımına eşittir.
- Dikdörtgenin alanı, uzun ve kısa kenar uzunluklarının çarpımına eşittir.
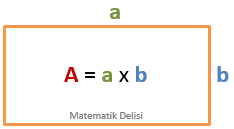
Bir dikdörtgenin genişliği “a” ve
yüksekliği “b” ise, alanını hesaplamak için aşağıdaki formülü kullanabiliriz.
A = a × b
Yukarıdaki dikdörtgenin alanını,
A = |KL| × |LM|
şeklinde de ifade edebiliriz.
Bir dikdörtgende karşılıklı kenar uzunlukları eşit olduğundan, aynı alanı
- |KL| × |KN|,
- |NM| × |LM| veya
- |NM| × |KN|
çarpımlarıyla da elde edebiliriz.
Genişliği 5 cm ve yüksekliği 3 cm olan bir dikdörtgenin alanını hesaplayalım.
a = 5 cm ve b = 3 cm değerlerini formülde yerlerine yazdığımızda, alanın 15 cm2'ye eşit olduğunu görebiliriz.
A = 5 cm × 3 cm = 15 cm2
Kenar uzunlukları cm cinsinden olduğu için alanın birimi cm2'dir.
Yukarıda gösterilen dikdörtgen şeklindeki arazinin alanını hesaplayalım.
A = |KL| × |LM| = 10 m × 5 m = 50 m2
Arazinin kenar uzunlukları metre cinsinden verildiği için sonuç m2 cinsinden çıkar.
Kenar uzunlukları farklı birimler cinsinden verildiğinde, çarpma yapmadan önce
bu birimlerden birini diğerine dönüştürürüz.
Uzunluk birimlerini birbirine nasıl dönüştürüldüğünü hatırlamak için bu bağlantıya
tıklayabilirsiniz.
Bir kenarı 20 cm ve diğer kenarı 0,3 m olan bir kartonun alanını bulalım.
Kenar uzunluklarından biri santimetre, diğeri ise metre cinsinden verilmiştir. Kenar uzunluklarını çarpmadan önce
- ya 20 cm’yi metreye
- ya da 0,3 m’yi santimetreye
dönüştürmemiz gerekir.
Ondalık gösterimlerde çarpma yapmayı henüz öğrenmediğimiz için 0,3 metreyi santimetreye dönüştürelim.
0,3 m = 30 cm
Aynı birime sahip uzunlukları formülde yerlerine koyup, alanı hesaplayalım.
A = 20 cm × 30 cm = 600 cm2
Aşağıdaki dikdörtgenlerin alanlarını bulun.
A = a × b formülü nereden geliyor?
Kenar uzunluğu 1 birim olan bir karenin alanının 1 birim2 olduğunu öğrenmiştik. Bu kareye, birim kare ismi verilir.
Şimdi, a ve b’nin birer doğal sayı olduğunu kabul edip, kenar uzunlukları a ve b birim olan bir dikdörtgeni, birim karelere bölelim.
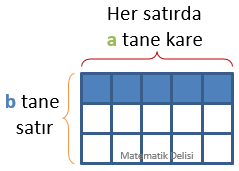
a doğal sayısı, a tane 1’in toplamına eşit olduğu için birim karelere bölünmüş dikdörtgenin bir satırında a tane kare olmalıdır. b doğal sayısı ise, b tane 1’in toplamıdır. Bu nedenle, karelere bölünmüş dikdörtgende b tane satır olmalıdır.
Dikdörtgende b tane satır ve her satırda a tane kare olduğundan, bu dikdörtgenin içerisinde toplam
a × b
tane birim kare vardır.
Bir birim karenin alanı 1 birim2 olduğu için dikdörtgenin alanı,
1 birim2 × a × b = a × b birim2'dir.
Kısa kenarı 3 m ve uzun kenarı 4 m olan bir dikdörtgeni, kenar uzunluğu 1 m olan karelere bölelim.
Karelere bölünen dikdörtgende 3 satır ve her satırda 4 kare bulunur. Buna göre, dikdörtgen toplam 4 × 3 = 12 kareden oluşur.
Bir karenin alanı 1 m2 olduğundan, toplam alan 12 m2'dir.
