BÖLÜM 2: DOĞRULARIN BİRBİRLERİNE GÖRE KONUMLARI
İki doğrunun birbirine göre konumunu belirlerken, üzerlerindeki noktalardan ne kadarının ortak olduğuna bakarız. Ortak veya kesişen nokta sayısına göre, bu konumu üç farklı şekilde tanımlayabiliriz.
A) ÇAKIŞAN DOĞRULAR
Tüm noktaları kesişen doğrular çakışan doğrulardır. İki doğrunun
çakışıp çakışmadığına bakarken bu doğruların her iki yönde sonsuza kadar uzandığını aklımızdan çıkarmamamız gerekir.
d ve e doğruları çakışmaktadır.
Yukarıdaki doğrular çakışmıyor gibi görünse de, bu doğruları her iki yönde de uzattığımızda tüm noktaların kesiştiğini, başka bir deyişle bu doğruların çakıştığını görebiliriz.
B) KESİŞEN DOĞRULAR
İki doğru yalnız bir noktada kesişiyorsa (yalnız bir noktaları ortaksa), bu doğrulara
kesişen doğrular ismini veririz.
Yukarıdaki AB ve CD doğruları yalnız bir noktada kesiştiği için bu doğrular kesişen doğrulardır.
İki doğrunun kesişip kesişmediğini anlayabilmek için bu doğruların her iki yönde sonsuza kadar
uzandığını aklımızda tutmamız gerekir.
Soldaki şekle göre doğrular kesişmiyor gibi görünse de, bu doğruların uzantılarını çizdiğimizde kesiştiklerini görebiliriz.
İki doğrunun kesişip kesişmediğini anlayabilmek için bu doğruların arasına birkaç tane dik
veya yatay çizgi çekebiliriz.
- Bu çizgilerin doğruların arasında kalan kısımları aynı uzunlukta değilse, doğrular bir yöne doğru birbirlerine yaklaşır ve yeterince uzatıldığında da kesişirler.
- Doğrular arasında kalan kısımlar aynı uzunluktaysa, bu doğruları ne kadar uzatırsak uzatalım kesişmezler.
Sol tarafa doğru gittikçe, yukarıdaki doğruların birbirine yaklaştığını görüyoruz. Aynı yönde yeterince uzatırsak bu doğrular kesişir. Bu nedenle, AB ve CD kesişen doğrulardır.
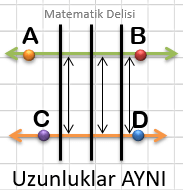
Yukarıdaki doğruların arasında kalan çizgilerin uzunluğu aynı. Hangi doğrultuda gidersek gidelim AB ve CD doğruları kesişmez.
Aşağıdaki doğrulardan hangilerinin kesiştiğini bulun.
Kesişen doğrular:
..AB ve CD.. ................... ................... ................... ...................
................... ................... ................... ................... ...................
C) PARALEL DOĞRULAR
Hiçbir noktada kesişmeyen doğrulara paralel doğrular denir.
AB ve CD doğruları birbirine paraleldir. Aynı zamanda EF ve GH doğruları da birbirine paraleldir.
AB doğrusu EF’ye veya GH’ye paralel değildir. Benzer şekilde, CD doğrusu da EF veya GH’ye paralel değildir.
İki doğru birbirine paralelse, bu doğruların isimlerinin arasına // sembolü koyarak paralel olduklarını gösterebiliriz.
Örneğin, önceki örnekte AB ve CD doğrularının paralel olduklarını, AB // CD ile gösterebiliriz.
Kesişen doğrularda yaptığımız gibi, verilen iki doğru arasına birkaç yatay veya dikey
çizgi çekerek bu doğruların paralel olup olmadığını anlayabiliriz. Eğer doğruların arasında kalan çizgilerin uzunlukları aynıysa, bu doğrular birbirine paraleldir.
AB ve CD doğruları arasında kalan çizgilerin uzunlukları aynı olduğu için bu doğrular paraleldir.
Hangi doğruların paralel olduğunu bulun.
Paralel doğrular:
...AB // CD... ................... ................... ................... ...................
