BÖLÜM 2: BASİT VE BİLEŞİK KESİRLERİ KARŞILAŞTIRMA
Basit ve bileşik kesirleri karşılaştırma yöntemlerini bu bölümde, tam sayılı kesirleri nasıl karşılaştıracağımızı ise bir sonraki bölümde görüyoruz.
A) PAYDA EŞİTLEME
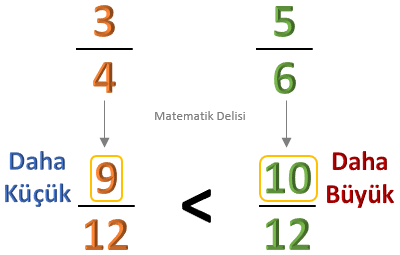
Basit ve bileşik kesirlerin karşılaştırılabilmesi için paydaları eşitlenebilir. Paydalar eşitlendiğinde,
büyük kesrin payı daha büyük çıkar.
... ile ... kesirlerini karşılaştıralım.
...’ü 2 ile genişleterek verilen kesirlerin paydalarını eşitleyebiliriz.
... ...
Paydaları eşit olan ... ve ... kesirlerinden payı daha büyük olan ...’dir. Bu nedenle ... kesri ...’den (ve dolayısıyla, ...’ten) büyüktür.
... > ...
... ile ... kesirlerini karşılaştıralım.
15 ile 18’in ortak katlarından en küçüğü 90’dır. Paydaları 90’da eşitleyebilmek için ilk kesri 90 ÷ 15 = 6 ve ikinci kesri 90 ÷ 18 = 5 ile genişletebiliriz. Genişletme işlemi sonrasında bu kesirler sırasıyla ... ve ... olur.
- ... ...
- ... ...
Paydalar eşitlendiğinde, değeri daha büyük olan kesrin payı daha büyük çıkar. Bu nedenle ... kesri ...’den büyüktür.
... > ...
Aşağıdaki kesirlerin aralarına “>” ve “<” işaretlerinden uygun olanı koyun.
a) ... ... ... b) ... ... ... c) ... ... ... d) ... ... ... e) ... ... ... f) ... ... ...
B) PAY-PAYDA ÇARPIMI
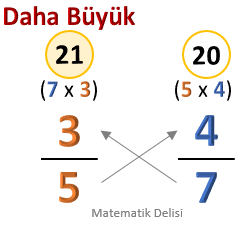
İki basit veya bileşik kesir karşılaştırılırken aşağıdaki adımlar izlenebilir.
- İlk kesrin üzerine, ikinci kesrin paydasıyla ilk kesrin payının çarpımı yazılır.
- İkinci kesrin üzerine, ilk kesrin paydasıyla ikinci kesrin payının çarpımı yazılır.
- Üzerinde büyük sayı yazan kesir daha büyüktür.
... ile ... kesirlerini karşılaştıralım.
Her bir kesrin payını diğer kesrin paydası ile çarpıp üzerine yazarsak, ilk kesrin üzerinde 65 ve ikinci kesrin üzerinde 72 sayısını elde ederiz.
72 daha büyük olduğundan ... kesri ...’den büyüktür.
... < ...
Bu yöntem aslında payda eşitleme yönteminin özel bir halidir. İki kesirden her biri, diğerinin paydası ile
genişletildiğinde, bu kesirlerin payları yukarıdaki yöntemde kesirlerin üzerine yazılan sayılara eşit olur.
Aşağıdaki kesirleri pay-payda çarpımı yöntemiyle karşılaştırıp aralarına “>” ve “<” işaretlerinden uygun olanı koyun.
a) ... ... ... b) ... ... ... c) ... ... ... d) ... ... ... e) ... ... ... f) ... ... ...
C) PAYI EŞİT OLAN KESİRLER
Payı eşit olan kesirlerden paydası büyük olanın değeri daha küçüktür.
... ile ... kesirlerini karşılaştıralım.
İlk kesrin paydası daha büyük olduğundan değeri daha küçüktür.
... < ...
..., ... ve ... kesirlerini karşılaştıralım.
Bu kesirlerin tümünün payı aynıdır. Bu nedenle paydası en küçük olan kesrin değeri en büyük ve paydası en büyük olan kesrin değeri en küçüktür. Buna göre doğru sıralama,
... > ... > ...
olmalıdır.
Aşağıdaki kesirleri karşılaştırın.
a) ... ... ... b) ... ... ... c) ... ... ... d) ... ... ... e) ... ... ...
D) BÜTÜNLER ÜZERİNDE GÖSTERME
Biraz uzun süren bir yöntem olsa da, verilen kesirleri modelleyen bütünler ve parçalar çizilerek bu kesirler
karşılaştırılabilir.
... ile ... kesirlerini karşılaştıralım.
... kesri 3 parçaya ayrılmış bir bütünün 2 parçasını; ... kesri ise, 4 parçaya ayrılmış bir bütünün 3 parçasını ifade eder.
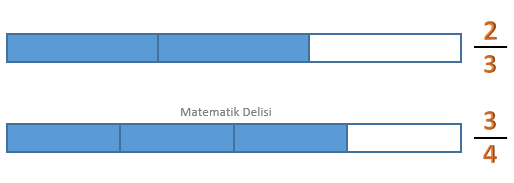
Görüldüğü gibi ... kesri 1’e daha yakın olduğu için daha büyüktür.
... > ...
... ile ... sayılarını karşılaştıralım.
3 sayısı, 3 tane bütünü ve ... kesri 7 tane yarımı ifade eder. Bu nicelikleri karşılaştırdığımızda, ...’nin daha büyük olduğunu görebiliriz.
... > ...
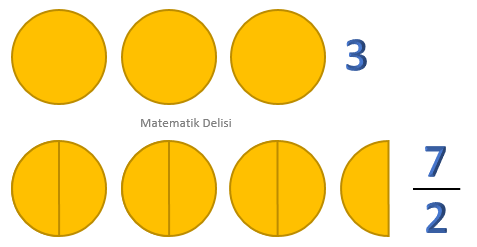
Aşağıdaki sayıları bütünler üzerinde göstererek karşılaştırın.
a) ... ... ... b) ... ... ... c) ... ... ... d) ... ... ... e) ... ... ... f) ... ... ...
E) ...’Yİ REFERANS ALMA
Bir kesrin ...’den büyük olup olmadığını
kolaylıkla anlayabiliriz.
- Payın 2 katı paydadan büyükse, kesir ...’den büyüktür.
- Payın 2 katı paydadan küçükse, kesir ...’den küçüktür.
Örneğin, ... kesrinde payın 2 katı 8 yapar. 8 sayısı paydadaki 7’den büyük olduğu için ... kesri ...’den büyüktür. ... kesrinde ise payın 2 katı paydadan küçük olduğu için ... kesri ...’den küçüktür.
Verilen iki kesirden biri
...’den büyük ve diğeri
...’den küçük çıkıyorsa,
...'den büyük olan kesir diğerinden de büyüktür.
... ile ... kesirlerini karşılaştıralım.
...’in payının 2 katı 6’dır. 6 sayısı paydadan küçük olduğundan, ... kesri ...'den küçüktür.
...’in payının 2 katı 26’dır. 26 sayısı paydadan büyük olduğundan, ... kesri de ...’den büyüktür.
Buna göre, ... kesri ...’den büyüktür.
... > ...
Aşağıdaki kesirleri karşılaştırın.
a) ... ... ... b) ... ... ... c) ... ... ... d) ... ... ... e) ... ... ... f) ... ... ...
ALIŞTIRMALARIN CEVAPLARI
a) ... > ..., b) ... > ..., c) ... > ..., d) ... < ..., e) ... < ..., f) ... > ...
a) ... > ..., b) ... > ..., c) ... < ..., d) ... > ..., e) ... > ..., f) ... > ...
a) ... > ..., b) ... < ..., c) ... > ..., d) ... > ..., e) ... > ...
a) ... < ..., b) ... < ..., c) ... > ..., d) ... > ..., e) ... > ..., f) ... > ...
a) ... > ..., b) ... > ..., c) ... < ..., d) ... > ..., e) ... > ..., f) ... < ...