BÖLÜM 1: KESİRLER (TEKRAR)
DENK KESİRLER
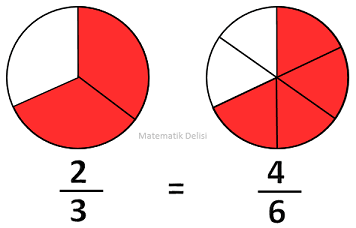
Aynı miktarı gösteren kesirler denktir. İki kesrin birbirine denk olduğu, aralarına “=” işareti
koyularak gösterilir.
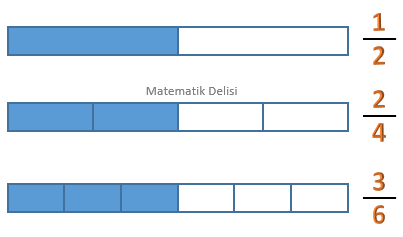
Bütünün aynı miktarını gösterdiği için ..., ... ve ... kesirleri denktir.
... ...
GENİŞLETME
Bir kesrin pay ve paydasının 0’dan farklı bir
... kesri
3 ile genişletildiğinde ... kesri elde edilir. ... ve ... kesirleri denktir.... ...
... kesri
6 ile genişletildiğinde ... kesri elde edilir. ... ve ... kesirleri denktir.... ...
... kesri
5 ile genişletildiğinde ... kesri elde edilir. ... ve ... kesirleri denktir.... ...
SADELEŞTİRME
Bir kesrin hem payının hem de paydasının 1’den büyük bir
Genellikle, payın ve paydanın ortak bölenlerinden biriyle sadeleştirme yapılır. Aksi takdirde, sadeleştirme sonucunda payı ve/veya paydası tam sayı olmayan bir kesir elde edilir.
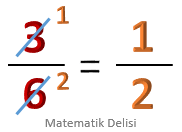
Sadeleştirme yapılırken, bölünen sayının üzeri çizilerek sağ üstüne işlem sonucu yazılır.
... kesri
5 ile sadeleştirildiğinde ... kesri elde edilir. ... ve ... kesirleri denktir....
... kesri
4 ile sadeleştirildiğinde ... kesri elde edilir. ... ve ... kesirleri denktir....
... kesri
3 ile sadeleştirildiğinde ... kesri elde edilir. ... ve ... kesirleri denktir....
Bir kesrin en sade halinin elde edebilmesi için mümkün olan tam sayıların tümüyle sadeleştirme yapılır.
... kesrinin en sade halini bulalım.
...
...
...
Eğer payın ve paydanın
...
Aşağıdaki kesirlerin en sade hallerini bulun.
a) ..., b) ..., c) ..., d) ..., e) ..., f) ...
PAYDALARI EŞİTLEME
Paydaları aynı olan kesirler arasında toplama, çıkarma ve karşılaştırma yapmak daha kolaydır. Bu işlemlerden biri yapılırken ilk aşamada paydalar eşitlenebilir.
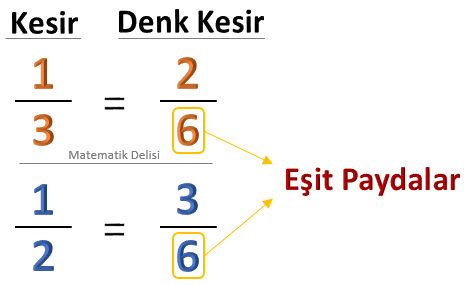
Kesirlerin paydalarını eşitlemek için bu kesirlere denk, eşit paydalı kesirler bulunur. Örneğin,
... ve
... kesirleri arasında toplama, çıkarma veya karşılaştırma yapmak için
... yerine bu kesre denk olan
... kesri ve
... yerine bu kesre denk olan
... kesri kullanılabilir. Böylece iki kesrin de paydası 6 olur.
Paydalar, ortak katlardan birine eşit olacak şekilde yapılan genişletmeler paydaların eşitlenmesine sağlar. İşlem kolaylığı açısından ortak katlardan en küçüğü seçilebilir.
... ile ... kesirlerinin paydalarını eşitleyelim.
Paydaların ortak katları 10, 20, 30, ...’dur. İki kesrin de paydası bu katlardan birine eşit olacak şekilde genişletme yapabiliriz. En küçük ortak kat olan 10’u seçtiğimizde ikinci kesirde genişletme yapmamız gerekmez. İlk kesri 10 ÷ 5 = 2 ile genişlettiğimizde ise ... kesrini elde ederiz.
... ...
Sonuç olarak, verilen kesirlerin paydalarını eşitlediğimizde ... ve ... kesirlerini elde ederiz.
... ile ... kesirlerinin paydalarını eşitleyelim.
4 ile 6’nın ortak katları 12, 24, 36 ...’dır. Paydaları bu katlardan 12’ye eşitleyebilmek için ...'ü 12 ÷ 4 = 3 ile ve ...’yı 12 ÷ 6 = 2 ile genişletmemiz gerekir.
- ... ...
- ... ...
Bu genişletmeleri yaptığımızda ... ve ... kesirlerini elde ederiz.
Ortak katlardan 24’ü seçseydik, ...‘ü 24 ÷ 4 = 6 ile ve ...’yı 24 ÷ 6 = 4 ile genişletmemiz gerekirdi.
- ... ...
- ... ...
Bu işlem sonucunda ise, ... ve ... kesirlerini elde ederiz.
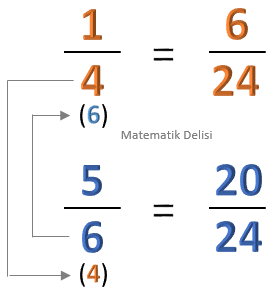
Ortak katların bulunup bu katlar arasından seçim yapılması yerine,
- birinci kesir ikinci kesrin paydası ile
- ikinci kesir birinci kesrin paydası ile
genişletilebilir. Yalnız bazı kesirler için çok büyük sayılar elde edileceğinden, bu yöntem genelde paydaların küçük olduğu veya ortak bölenlerinin olmadığı durumlarda kullanılır.
... ile ... kesirlerinin paydalarını eşitleyelim.
...'ü diğer kesrin paydası olan
... ...
...’i de
...'ün paydası olan
... ...
Böylece eşit paydalı iki kesir elde ettik.
Verilen kesirlerin paydalarını eşitleyin.
a) ... ve ...
b) ... ve ...
c) ... ve ...
d) ... ve ...
e) ... ve ...
ALIŞTIRMALARIN CEVAPLARI
a) ..., b) ..., c) ..., d) ..., e) ..., f) ...
a) ..., b) ..., c) ..., d) ..., e) ..., f) ...
a) ... ve ..., b) ... ve ..., c) ... ve ..., d) ... ve ..., e) ... ve ...