BÖLÜM 2: TAM SAYILI KESİRLERLE TOPLAMA
BİLEŞİK KESRE DÖNÜŞTÜREREK TOPLAMA
Tam sayılı kesirlerle toplama yapmadan önce bu kesirleri bileşik kesre dönüştürebiliriz. Böylece
önceki bölümde öğrendiğimiz adımları uygulayarak sonuca ulaşabiliriz.
... işleminin sonucunu bulalım.
İşlemdeki tam sayılı kesirleri bileşik kesre dönüştürelim.
... ...
Paydaları en küçük ortak kat olan 24’te eşitleyebilmek için ilk kesri 3 ve ikinci kesri 4 ile genişletelim.
... ...
Genişlettiğimiz kesirleri toplayalım.
... ...
Bulduğumuz sonucu tam sayılı kesre de dönüştürebiliriz.
...
- ... ... ... ...
- ... ... ... ...
- ... ... ...
- ... ... ... ... ...
TAM VE KESİRLİ KISIMLARI AYRI AYRI TOPLAMA
Tam sayılı kesirleri toplarken,
- Tam kısımları kendi aralarında toplayıp, sonucun tam kısmına ve
- Kesirli kısımları kendi aralarında toplayıp, sonucun kesirli kısmına
yazabiliriz.
... işleminin sonucunu bulalım.
Tam kısımları toplamı 5’e ve kesirli kısımların toplamı ...’e eşittir.
- ...
- ... ... ...
Bu sayıları sonucun tam ve kesirli kısımlarına yazdığımızda ... kesrini elde ederiz.
...
NEDEN?
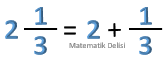
♠ Bir tam sayılı kesir, tam ve kesirli kısımlarının toplamına eşittir.
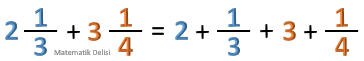
♣ Toplama işlemindeki her tam sayılı kesrin yerine, tam ve kesirli kısımların toplamını yazdığımızda, karşımıza bir grup tam sayı ile bir grup kesrin toplamı çıkar.
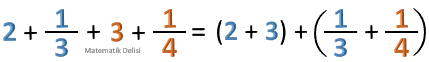
♥ Tam sayıları kendi aralarında ve kesirleri kendi aralarında toplamamız, bir tam sayı ve bir kesrin toplamına erişmemizi sağlar.
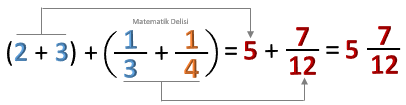
♦ Bu iki sayının toplamı ise bir tam sayılı kesre eşittir.
- ...
- ... ... ...
- ... ... ...
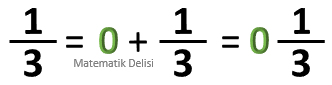
Bir basit veya bileşik kesri, tam kısmı 0 olan bir tam sayılı kesir gibi düşünebiliriz.
... işleminin sonucunu bulalım.
İkinci kesrin tam kısmı olmadığı için tam kısımların toplamı ilk kesrin tam kısmına eşittir. Kesirli kısımların toplamı ise ...’dır.
...
Buna göre, işlem sonucu ...’ya eşittir.
...
Bir tam sayıyı, kesirli kısmı 0 olan tam sayılı kesir gibi düşünebiliriz.
... işleminin sonucunu bulalım.
Tam kısımların toplamı 2 + 4 = 6’dır. İşlemdeki ikinci sayı bir tam sayı olduğu için kesirli kısımların toplamı ilk kesrin kesirli kısmına eşittir. Dolayısıyla, işlem sonucu ...'tür.
...
Aşağıdaki işlemlerin sonucunu bulun.
a) ..., b) ..., c) ..., d) ..., e) ..., f) ..., g) ...
Kesirli kısımların toplamı bir bileşik kesre eşit çıkabilir. Bu durumda elde ettiğimiz bileşik kesri tam sayılı kesre
dönüştürebiliriz. Bulduğumuz kesirli kısmı, sonucun kesirli kısmına yazar, tam kısmı ise diğer kesirlerin tam kısmına ekleriz.
... işleminin sonucunu bulalım.
Tam kısımları toplamı 5’e ve kesirli kısımların toplamı ...’ya eşittir.
- ...
- ... ... ...
Bu sayıları sonucun tam ve kesirli kısımlarına yazdığımızda ... kesrini elde ederiz. Kesirli kısım bir bileşik kesir olduğu için bu kısmı tam sayılı kesre dönüştürebiliriz.
...
Bu kesrin tam kısmını yukarıda bulduğumuz tam kısma eklediğimizde 5 + 1 = 6 sayısı çıkar. 6’yı tam kısma ve ...’yı kesirli kısma yazdığımızda ... kesrini elde ederiz.
...
- ... ... ...
- ... ... ...
- ... ... ...
- ... ... ...
Toplama sonucunda kesirli kısmın değeri bir doğal sayıya eşitse, bu değeri tam kısma ekleriz.
- ... ... ...
- ... ... ...
- ... ... ...
DİĞER HESAPLAMA ARAÇLARI
ALIŞTIRMALARIN CEVAPLARI
a) ..., b) ..., c) ..., d) ..., e) ...
a) ..., b) ..., c) ..., d) ..., e) ..., f) ..., g) ...
a) ..., b) ..., c) ..., d) ..., e) ...