BÖLÜM 3: ORTAK BÖLENLER VE KATLARLA İLGİLİ PROBLEMLER

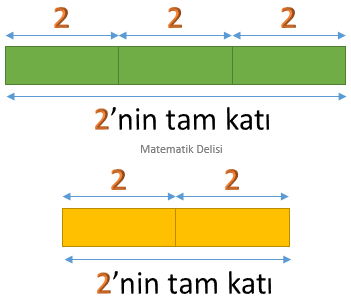
Uzunluğu, hacmi veya ağırlığı verilen iki bütünün eşit parçalara bölünebilmesi için bütünlerden her birinin, parça büyüklüğünün tam katı olması gerekir. Başka bir deyişle, parça büyüklüğünün bütünlerin ortak böleni olması gerekir.

ÖRNEK:

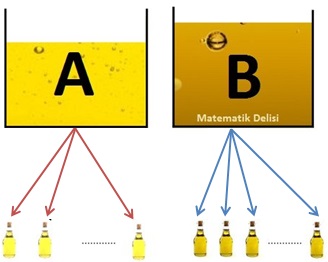
Hacimleri 18 litre ve 21 litre olan iki çeşit zeytinyağı, artmayacak ve birbiriyle karışmayacak şekilde eşit hacimli şişelere doldurulacaktır. Bu iş için kaç litrelik şişeler kullanılabilir?

A) 2 B) 3 C) 5 D) 6

ÇÖZÜM:

A) 21 litre zeytinyağıyla 2 litrelik 10 şişe tam olarak doldurulabildiği halde, geriye 1 litre yağ kalır. Dolayısıyla, bu iş için 2 litrelik şişeler kullanılamaz. 2 sayısı 21'in böleni değildir.

B) 18 litre zeytinyağı 3 litrelik 18 ÷ 3 = 6 şişeye ve 21 litre zeytinyağı 3 litrelik 21 ÷ 3 = 7 şişeye tam olarak sığar. Bu iş için 3 litrelik şişeler kullanılabilir. 3 sayısı 18 ve 21'in ortak bölenidir.

C) Ne 18 ne de 21 litre zeytinyağıyla 5 litrelik şişeler tam olarak doldurulabilir. Her iki durumda da bir miktar zeytinyağı artar. 18 de 21 de 5'e kalansız bölünmez.

D) 18 litre yağla 6 litrelik 3 şişe tam olarak doldurulabilse de 21 litre yağla 6 litrelik şişelere artmayacak şekilde dolum yapılamaz. 6 sayısı 21'i tam bölmez.

Kullanılacak şişenin litre cinsinden hacmi, 18 ve 21'in ortak böleni olmalıdır.

ÖRNEK:

Bir okulun 6-A ve 6-B şubelerindeki öğrenci sayıları sırasıyla 30 ve 36'dır. Bu öğrencilerin tümü aynı sayıda öğrenciden oluşan gruplara ayrılacak ve oluşturulan gruplar arasında bir yarışma düzenlenecektir. Bir grupta en az 2 öğrencinin olması ve aynı gruptaki öğrencilerin aynı şubeden olması gerekiyorsa, yarışmaya toplam kaç grup katılabilir?

Farklı şubelerden öğrencilerle grup oluşturulamadığı için 6-A şubesindeki 30 öğrenci kendi arasında ve 6-B şubesindeki 36 öğrenci de kendi arasında gruplara ayrılacaktır.

30 öğrencinin kendi arasında her grupta aynı sayıda öğrenci olacak şekilde gruplara ayrılabilmesi, ancak gruplardaki öğrenci sayılarının 30'un böleni olduğunda mümkündür. Aynı sayıda öğrenciden oluşan gruplar B şubesinde de oluşturulacağından, bir gruptaki öğrenci sayısının aynı zamanda 36'nın da böleni olması gerekir. Özetle, bir gruptaki öğrenci sayısı 30 ve 36'nın ortak bölenidir.

30'un bölenleri: 1, 2, 3, 5, 6, 10, 15 ve 30
36'nın bölenleri: 1, 2, 3, 4, 6, 9, 12, 18 ve 36

30 ve 36'nın ortak bölenleri 1, 2, 3 ve 6'dır. 1 öğrenci ile grup oluşturulamayacağından gruplar 2, 3 veya 6 öğrencili olabilir.

2 kişilik gruplar oluşturulduğunda, A şubesinden 30 ÷ 2 = 15 ve B şubesinden 36 ÷ 2 = 18 grup çıkar ve toplam grup sayısı 15 + 18 = 33 olur.
Her grupta 3 öğrencinin bulunduğu durumda ise A şubesinden 30 ÷ 3 = 10 ve B şubesinden 36 ÷ 3 = 12 grup çıkar. Bu durumda toplam grup sayısı 10 + 12 = 22 olur.
6 öğrencinin bir grup oluşturduğu son durumda da A şubesindeki grup sayısı 30 ÷ 6 = 5 ve B şubesindeki grup sayısı 36 ÷ 6 = 6 olur. Toplam grup sayısı ise 5 + 6 = 11 olarak bulunur.

Özetle, grup sayısı 33, 22 veya 11 olabilir.

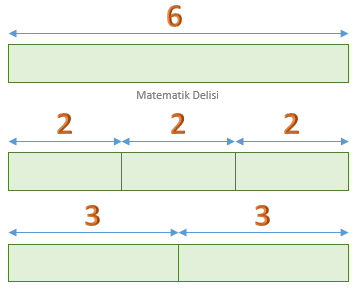
Bir bütün hem a hem de b birimlik eşit parçalara ayrılabiliyorsa, bu bütünün büyüklüğü aynı birim cinsinden a ve b sayılarının ortak katıdır.

ÖRNEK:

300’den fazla ve 500’den az turist barındırdığı bilinen bir kafiledeki yolcular 18 yolcu kapasitesine sahip minibüslerle de taşınsa, 20 yolcu kapasitesine sahip minibüslerle de taşınsa kullanılan araçların tümü tam olarak dolmaktadır. Buna göre, kafiledeki turist sayısı kaçtır?

Toplam turist sayısını bir bütün olarak düşündüğümüzde bu bütünün hem 18 hem de 20 kişilik eşit gruplara ayrılabildiğini görüyoruz. Bu nedenle kafiledeki turist sayısı 18 ve 20 sayılarının ortak katlarından biridir. 18 ile 20’nin ortak katları 180, 360, 540 …’tır. 300’den büyük ve 500’den az olan tek ortak kat 360 olduğu için kafiledeki turist sayısı da 360’tır.

ÖRNEK:

Ali her üç güne bir, Ayşe'yse her dört güne bir sinemanın 11 matinesindeki filmi izlemeye gitmektedir. Sürekli aynı sinema salonuna gitmeyi tercih eden Ali ve Ayşe, 1 Ekim'de bu salonda karşılaşmıştır. Buna göre, Ali ile Ayşe ekim ayı içerisinde kaç defa aynı gün sinemaya gitmiştir?

Ali her üç güne bir sinemaya gittiği için burada izlediği herhangi iki film arasında geçen gün sayısı 3'ün tam katıdır. Benzer şekilde, Ayşe'nin izlediği herhangi iki film arasında geçen gün sayısı da 4'ün tam katıdır. Dolayısıyla, Ali ve Ayşe'nin sinemada karşılaştıkları zamanlar arasında geçen gün sayısı 3 ve 4'ün ortak katıdır. 3 ve 4 sayılarının ortak katları 12, 24, 36, ...'dır. İlk kez Ekim ayının 1'inde karşılaşan Ali ile Ayşe, aynı ay içerisinde 12 gün sonra 13 Ekim'de ve 24 gün sonra 25 Ekim'de tekrar karşılaşırlar. Buna göre, ekim ayı içerisinde toplamda 3 kez aynı gün sinemaya giderler.

→KONU ANASAYFASINA DÖN←

ÖNCEKİ BÖLÜM

BÖLÜM 2: ORTAK KATLAR

SONRAKİ KONU

KÜMELER