BÖLÜM 3: AÇIKLIK VE ARİTMETİK ORTALAMA
Bir veri grubunun açıklığı, bu gruptaki en büyük ve en küçük veriler arasındaki farka eşittir.
Bir veri grubunun aritmetik ortalaması, verilerin toplamının veri sayısına bölümüne eşittir.
Bir şirketteki çalışan sayısının yıllara göre değişimi aşağıdaki tabloda gösterilmiştir.
| Yıllar | Çalışan Sayısı |
|---|---|
| 53 | |
| 59 | |
| 49 | |
| 55 |
Tablo: A şirketinin yıllara göre çalışan sayısı
Açıklık:
Bu tablodaki en büyük ve en küçük veriler, sırasıyla, 59 ve 49'dur. Dolayısıyla, yukarıdaki veri grubunun açıklığı 59 – 49 = 10'dur.
Açıklık = ...
Aritmetik Ortalama:
Yukarıdaki tabloda 4 veri görüyoruz. Bu verileri toplayıp 4'e bölerek aritmetik ortalamayı bulabiliriz.
Aritmetik Ortalama = ... ...
Hafta içi her gün bir oyun sergilenen bir tiyatro salonuna geçen hafta gelen izleyici sayıları aşağıdaki sütun grafiğinde gösterilmiştir.
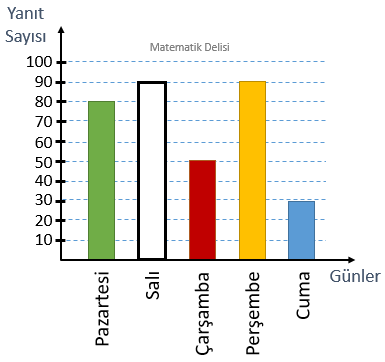
Açıklık:
Bu veri grubunun en büyük ve en küçük değerleri, sırasıyla, 90 ve 30'dur. Buna göre, yukarıdaki veri grubunun açıklığı 90 – 30 = 60'tır.
Açıklık = ...
Aritmetik Ortalama:
Grafikteki verileri toplayıp, 5'e böldüğümüzde aritmetik ortalamanın 68 olduğunu görebiliriz.
Aritmetik Ortalama = ... ...
Sütun grafiği veya tabloyla gösterilen aşağıdaki veri gruplarının açıklıklarını ve aritmetik ortalamalarını hesaplayın.
A)
B)
| En Sevilen Renk | Yanıt Sayısı |
|---|---|
| 10 | |
| 15 | |
| 23 |
C)
D)
| Yayınevi | Kitap Sayısı |
|---|---|
| 15 | |
| 25 | |
| 39 | |
| 21 |
İkili sıklık tablolarında ve sütun grafiklerinde iki farklı veri grubuna ait veriler gösterilmektedir. Bu iki veri
grubunun kendi içlerinde açıklıklarını ve aritmetik ortalamalarını hesaplayıp birbiriyle karşılaştırabiliriz.
Bir koşucu olan Ali'nin 2018 ve 2019 yıllarında aldığı madalya sayıları aşağıdaki tabloda gösterilmiştir.
| Madalya | Madalya Sayısı | |
|---|---|---|
| 2018 | 2019 | |
| 7 | 8 | |
| 5 | 4 | |
| 9 | 12 | |
Tablo: Ali'nin son iki yılda aldığı madalyalar
Açıklıklar:
- 2018 yılına ait verilerin en yükseği 9 ve en düşüğü 5'tir. Bu veri grubunun açıklığı 9 – 5 = 4'tür.
- 2019 yılına ait verilerin en yükseği 12 ve en düşüğü 4'tür. Bu veri grubunun açıklığı 12 – 4 = 8'dir.
Aritmetik Ortalamalar:
- 2018 yılına ait verilerin aritmetik ortalaması ...'dir.
- 2019 yılına ait verilerin aritmetik ortalaması ...'dir.
Elektronik ve yazılım alanlarında iş yapan bir firmanın aylara göre farklı faaliyet alanlarında elde ettiği gelirleri gösteren sütun grafiği aşağıdaki gibidir.
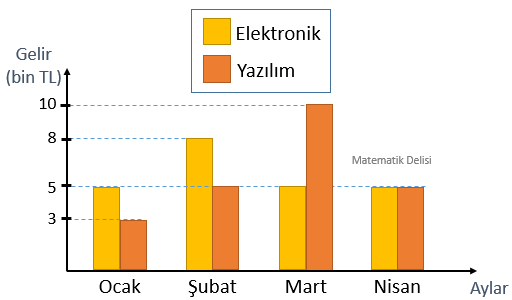
Açıklıklar:
- Elektronik alanındaki gelirlerin en yükseği 8 bin TL ve en düşüğü 5 bin TL'dir. Bu alandaki verilerin açıklığı 8 bin – 5 bin = 3 bin TL'dir.
- Yazılım alanındaki en yüksek gelir 10 bin TL ve en düşük gelir 3 bin TL olduğu için bu veri grubunun açıklığı 10 bin – 3 bin = 7 bin TL'dir.
Aritmetik Ortalamalar:
Elektronik alanındaki gelirlerin aritmetik ortalaması
... ... TL'dir.
Yazılım alanındaki gelirlerin aritmetik ortalaması
... ... TL'dir.
Aşağıdaki sütun grafiklerinde ve tablolarda gösterilen veri gruplarının açıklıklarını ve aritmetik ortalamalarını bulun.
A)
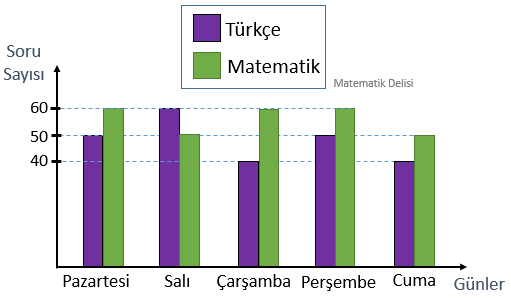
B)
| En Sevilen Ders | Yanıt Sayısı | |
|---|---|---|
| 5. Sınıf | 6. Sınıf | |
| 15 | 18 | |
| 10 | 5 | |
| 5 | 7 | |
C)
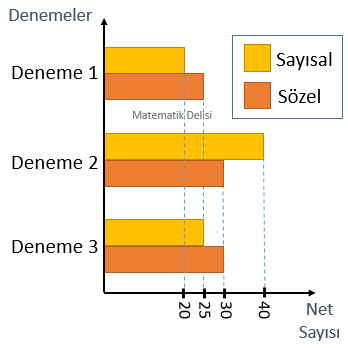
D)
| Favori Kanal | Yanıt Sayısı | |
|---|---|---|
| Evli | Bekar | |
| 15 | 7 | |
| 10 | 23 | |
| 12 | 20 | |
| 15 | 8 | |