BÖLÜM 3: KESİRLİ İŞLEMLERİN SONUCUNU TAHMİN ETME
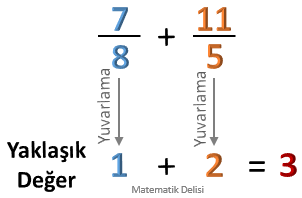
Kesirlerle yapılan işlemlerde, sonucu tahmin edebilmek için kesirleri uygun sayılara
yuvarlar, işlemleri bu sayılarla gerçekleştiririz.
... işleminin sonucunu tahmin edelim.
- ... kesrini ...’ye ve
- ... kesrini ...’e
yuvarlayabiliriz. İşlemdeki kesirlerin yerine yuvarlama yaparak elde ettiğimiz sayıları koyduğumuzda, bu işlem aşağıdaki hale dönüşür.
...
Yukarıdaki toplama işlemini zihinden yapıp sonucun ...'ye veya veya “1 buçuğa” eşit olduğunu söyleyebiliriz.
Aynı işlemi kesirleri yuvarlamadan gerçekleştirdiğimizde ise 1 buçuğa yakın bir sayı olan ... kesrini elde ederiz.
... işleminin sonucunu tahmin edelim.
İşlemdeki bileşik kesirleri tam sayılı kesre dönüştürelim.
- ...
- ...
Bulduğumuz kesirleri tam veya buçuklu sayılara yuvarlayalım.
- ...’ün kesirli kısmı ...’ye yakın olduğu için bu kesri ...’ye yuvarlayabiliriz.
- ..., buçuklu bir sayı olduğu için bu kesri işlemde yuvarlama yapmadan da kullanabiliriz.
Elde ettiğimiz sayıları yerlerine yazdığımızda, aşağıdaki işlemle karşılaşırız.
...
Bu işlemin sonucu ...’ye eşittir.
Sorudaki işlemi yuvarlama yapmadan gerçekleştirdiğimizde ise ... sonucunu elde ederiz.
Aşağıdaki işlemlerin yaklaşık sonucunu bulun.
a) ... b) ... c) ... d) ... e) ... f) ...
g) ... h) ... i) ... j) ... k) ... l) ...
m) ... n) ... o) ... p) ... r) ... s) ...
Kesirleri sadece tam sayılara yuvarlayarak da yaklaşık sonuçlar elde edebiliriz.
... işleminin sonucunu tahmin edelim.
- ...’ye en yakın tam sayı 8’dir.
- ...’e en yakın tam sayı 3’tür.
8 . 3 = 24 olduğundan işlem sonucunu 24 olarak tahmin edebiliriz. Sorudaki işlemin gerçek sonucu ise ...’dir.
... işleminin sonucunu tahmin edelim.
- ...’ye en yakın tam sayı 15’tir.
- ...’e en yakın tam sayı 3’tür.
Bulduğumuz tam sayıları kullandığımızda işlem sonucu 15 ÷ 3 = 5 olur. Gerçek sonuç ise, ...’tür.
ÇEYREĞE VE ...'E YUVARLAYARAK YAPILAN İŞLEMLER
Bazı çarpma veya bölme işlemlerinde kesirleri
... yerine
...'e (çeyreğe) veya
...’e yuvarlayarak tanımlı ve gerçeğe daha yakın bir sonuç elde edebiliriz.
... işleminin sonucunu tahmin edelim.
... kesrinin yaklaşık değeri ...’dir. ... kesri ise ..., ... ve ... sayılarından en fazla ...’a yakındır. Bu sayıları yerlerine yazdığımızda ... işlemini elde ederiz. ...’a bölme işlemi tanımsız olduğu için yaptığımız yuvarlamalar bize yaklaşık bir değer vermez. ... kesrini, bu kesre yakın olan ...’e (çeyreğe) yuvarladığımızda ise işlem sonucu ... çıkar. Gerçek işlem sonucu ise ...’tür.
... işleminin sonucunu tahmin edelim.
İkinci çarpanı bir tam sayılı kesre dönüştürdüğümüzde ... kesrini elde ederiz. Bu kesir yaklaşık olarak ...’e eşittir. ... kesri ise ..., ... ve ... sayılarından en fazla ...’ye yakındır. Yuvarlama sonucunda elde ettiğimiz sayıları işlemde yerlerine koyduğumuzda ... (1 buçuk) sonucuna ulaşırız.
Yalnız ... kesrini, bu kesre yakın olan ...’e yuvarladığımızda gerçek sonuca daha yakın bir sonuç elde ederiz.
... olduğundan işlem sonucunun yaklaşık olarak ... olduğunu söyleyebiliriz. Yuvarlama yapmadığımız taktirde işlem sonucu ... çıkar. Bu sayı, 1'e 1 buçuktan daha yakındır.
ALIŞTIRMALARIN CEVAPLARI
a) ..., b) ..., c) ..., d) ..., e) ..., f) ..., g) ..., h) ..., i) ..., j) ..., k) ..., l) ..., m) ..., n) ..., o) ..., p) ..., r) ..., s) ...
a) ..., b) ..., c) ..., d) ..., e) ...