BÖLÜM 1: BASİT KESİRLERİ YUVARLAMA
![]() Bir kesri yuvarlarken
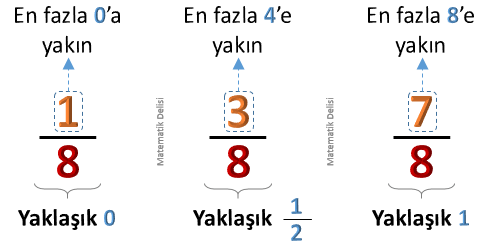
Bir kesri yuvarlarken
- 0’a yakınsa, kesri ...’a;
paydasının yarısına yakınsa, kesri ...'ye;paydasına yakınsa, kesri ...’e
yuvarlayabiliriz. (Bu yuvarlama yönteminin nedenini görmek için buraya tıklayabilirsiniz.)
![]()
... kesrini yuvarlayalım.
Bu kesrin
- paydası 8'e ve
- paydasının yarısı 8 ÷ 2 = 4’e eşittir.
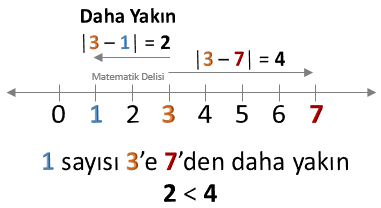
Yuvarlama yapabilmek için paydaki 7’nin, 0, 4 ve 8 sayılarından hangisine daha yakın olduğunu belirlememiz gerekir. 7 ile bu sayılar arasındaki farkların mutlak değeri aşağıdaki gibidir.
- |7 – 0| = |7| = 7
- |7 – 4| = |3| = 3
- |7 – 8| = |–1| = 1
En küçük sonucu 8 verdiği için kesrin payı bu üç sayıdan en fazla 8’e yakındır. Dolayısıyla, soruda verilen kesir 1’e yuvarlanabilir.
...
... kesrini yuvarlayalım.
Bu kesrin paydası 5’e ve paydasının yarısı 2,5’e eşittir.
- |2 – 0| = 2
- |2 – 2,5| = 0,5
- |2 – 5| = 3
2 sayısı, 0, 2,5 ve 5 arasından en fazla 2,5’e yakın olduğu için soruda verilen kesri ...'ye yuvarlayabiliriz.
...
... kesrini yuvarlayalım.
Bu kesrin paydası 7’ye ve paydasının yarısı 3,5’e eşittir.
Kesrin payı, 0, 3,5 ve 7 sayılarından en fazla 0’a yakındır. Bu nedenle, ... kesri 0’a yuvarlanabilir.
...
- ... kesri ... ile ...’nin,
- ... kesri ise ... ile ...’in
tam ortasındadır. Bu kesirleri, doğal sayılarda olduğu gibi yukarı yuvarlayabiliriz. Başka bir deyişle, ...’e denk olan kesirleri ...‘ye ve ...‘e denk olan kesirleri ...’e yuvarlayabiliriz.
... kesrini yuvarlayalım.
Paydaki 6 sayısı, paydadaki 8’e ve 8'in yarısı olan 4’e eşit uzaklıktadır. Payı 8’e yuvarladığımızda, kesir 1’e eşit olur.
...’e denk olan bu kesri 1’e yuvarlayabiliriz.
...
Aşağıdaki kesirleri ..., ... ve ... sayılarından en uygun olana yuvarlayın.
a) ... b) ... c) ... d) ... e) ... f) ... g) ... h) ... i) ...
ÇEYREĞE VE ÜÇTE BİRE YUVARLAMA
![]() Üçüncü bölümde, kesirleri
... yerine
... veya
...’e yuvarlamanın bazı işlemlerde gerçeğe daha yakın sonuçlar verdiğini görüyoruz.
Üçüncü bölümde, kesirleri
... yerine
... veya
...’e yuvarlamanın bazı işlemlerde gerçeğe daha yakın sonuçlar verdiğini görüyoruz.
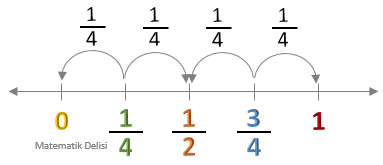
Payı paydasının üçte birine yakın olan bir kesri ...’e ve dörtte birine yakın bir kesri ...’e (çeyreğe) yuvarlayabiliriz.
- ...
- ...
- ...
- ...
ALIŞTIRMALARIN CEVAPLARI
a) ..., b) ..., c) ..., d) ..., e) ..., f) ..., g) ..., h) ..., i) ...
YUVARLAMA KURALININ NEDENİ
Doğal sayılarla toplama, çarpma gibi işlemler yaparken sonucu tahmin edebilmek için verilen sayıları en yakın onluklara, yüzlüklere vs. yuvarlarız. Çünkü yuvarlama sonucunda, daha kolay işlem yapmamızı sağlayan bir sayı elde ederiz. Örneğin, 82 . 38 işlemini tahmin edebilmek için çarpanları en yakın onluklara yuvarladığımızda, 80 . 40 gibi kolay bir işlemle karşılaşırız. Aynı bir mantığı kesirli sayı içeren işlemler için de uygulayabiliriz. İşlemdeki kesirleri ...'ye veya en yakın tam sayıya yuvarladığımızda, bu işlem zihinden gerçekleştirebileceğimiz bir hale dönüşebilir.
Bir basit kesri ...’a, ...’ye veya ...’e yuvarlayabiliriz. Bir basit kesir bu değerleri aşağıdaki koşullarda alır.
- Kesrin payı 0’a eşitse, değeri de 0’a eşittir.
- Kesrin payı paydasına eşitse, değeri 1’e eşittir.
- Kesrin payı paydasının yarısına eşitse, değeri ...'ye eşittir.
Buna göre, kesrin payını 0, paydanın yarısı ve paydayla karşılaştırarak değerinin 0, ... ve 1 sayılarından hangisine daha yakın olduğunu anlayabiliriz.