BÖLÜM 6: DAİRE GRAFİĞİ
Daire grafiğinde bütünü tam daireyle ve
bütünü oluşturan parçaları daire dilimleriyle gösteriyoruz.
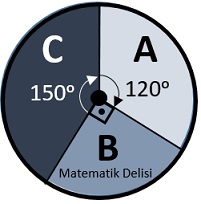
Bir parçaya ait daire diliminin büyüklüğü, bu parçanın bütüne olan
oranına bağlıdır. Parçanın bütüne oranı ne kadar büyükse, daire diliminin açısı da o kadar büyük olur.
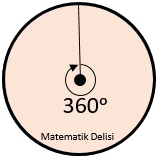
Tam daire 360° olduğu için aşağıdaki doğru orantıyı kurarak, bir parçaya ait daire
diliminin merkez açısını bulabiliriz.
Yukarıdaki orantıyı kullanarak, aşağıdaki formülü elde edebiliriz.
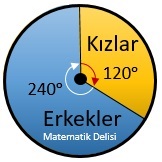
10 kız ve 20 erkek öğrenciden oluşan bir sınıftaki kız ve erkek öğrenci dağılımını gösteren daire grafiğini çizelim.
Sınıfı temsil eden bir tam daireyi, biri kız ve diğeri erkek öğrencileri gösterecek şekilde iki dilime ayıracağız. Sınıfın tamamı 10 + 20 = 30 kişi olduğu için bütünü 30; kız ve erkek öğrencileri gösteren parçaları ise, sırasıyla, 10 ve 20 olarak almamız gerekir.
(Bütün: 30, Kızlar: 10, Erkekler:20)
Kızları gösteren daire diliminin merkez açısı:
...
Erkekleri gösteren daire diliminin merkez açısı:
...
Bulduğumuz açılara göre daireyi dilimlere ayırıp, her dilimi farklı bir renkle gösterelim.
Merkez açıların kaçar derece olduğunu ve hangi dilimin hangi veriyi gösterdiğini grafik üzerinde belirtelim.
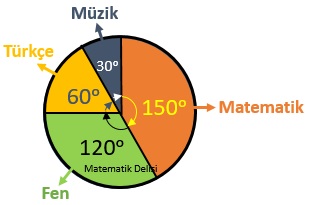
| En Sevilen Ders | Yanıt Sayısı |
|---|---|
| Matematik | 10 |
| Fen | 8 |
| Türkçe | 4 |
| Müzik | 2 |
Bir sınıftaki öğrencilere en sevdikleri ders sorulmuş ve alınan yanıtlara göre yukarıdaki sıklık tablosu oluşturulmuştur. Bu sonuçları daire grafiğinde gösterelim.
Soruya yanıt veren öğrencilerin sayısı 10 + 8 + 4 + 2 = 24'tür.
(Bütün: 24)
Yukarıdaki formülü kullanarak, yanıtlara karşılık gelen daire dilimlerinin merkez açılarını bulalım.
- Matematik: ...
- Fen: ...
- Türkçe: ...
- Müzik: ...
Bulduğumuz açılara göre daire grafiğini aşağıdaki gibi dilimlere ayırabiliriz.
Aşağıdaki verileri daire grafiği ile gösterelim.
A)
| Takım | Topa Hakim Olunan Süre (dk) |
|---|---|
| 60 | |
| 30 |
B)
| Ülke | Turist Sayısı |
|---|---|
| 7000 | |
| 2000 | |
| 1000 |
C)
| Balık Türü | Balık Sayısı |
|---|---|
| 60 | |
| 200 | |
| 50 | |
| 50 |
D)
| İçerik | Kütle (mg) |
|---|---|
| Yağ | 50 |
| 25 | |
| 15 | |
| 30 |
YÜZDELER VE DAİRE GRAFİĞİ
Sadece bütüne ait parçaların yüzdelerini kullanarak da daire grafiği oluşturabiliriz.
360°'nin % 1'i 3.6°'ye eşit olduğu için
bir bütüne ait her % 1'lik parçayı, daire grafiğindeki 3.6°'lik bir dilimle ifade ederiz.
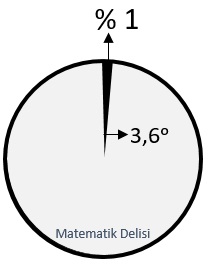
Bir parçanın yüzdesini 3.6° ile çarparak bu parçaya ait daire diliminin merkez açısını bulabiliriz.
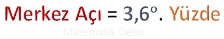
Bir ürünün satış fiyatının % 50'sinin hammadde masraflarına, %10'unun işçilik ücretlerine ve %15'inin vergilere gittiğini; geri kalan %25'inin ise üretim yapan firmaya kâr olarak kaldığını düşünelim. Bu ürünün satışından elde edilen paranın dağılımını daire grafiği ile gösterelim.
Yüzde ile ifade edilen oranların her birini 3.6° ile çarparak daire grafiğindeki dilimlerin merkez açılarını hesaplayalım.
- Hammadde masrafları: 3.6° × 50 = 180°
- İşçilik: 3.6° × 10 = 36°
- Vergiler: 3.6° × 15 = 54°
- Kâr: 3.6° × 25 = 90°
Bulduğumuz açılara göre daire grafiğini dilimlere ayıralım.
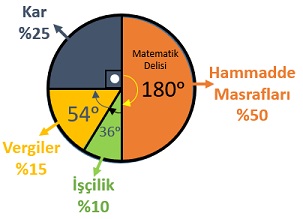
Yüzdelerle ifade edilen parçaları daire grafiğinde gösterelim.
A)
Okyanuslar: %75
Denizler: %15
Nehirler ve Göller: %10
B)
| Madde | Karışım Yüzdesi |
|---|---|
| % 40 | |
| % 30 | |
| % 20 | |
| % 10 |
C)
| Renk | Yüzde |
|---|---|
| % 30 | |
| % 30 | |
| Sarı | % 40 |
Daire grafiğindeki yüzdeleri bulabilmek için merkez açıları 3.6°'ye bölmemiz gerekir.
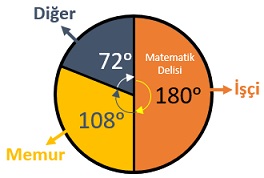
Yukarıdaki daire grafiğinde gösterilen daire dilimlerinden her birinin bütünün yüzde kaçına denk geldiğini bulalım.
- İşçiler: ... olduğundan, işçiler tüm grubun % 50'sidir.
- Memurlar: ... olduğundan, memurlar tüm grubun % 30'udur.
- Diğer: ... olduğundan, diğer kategorisindeki kişiler tüm grubun % 20'sidir.
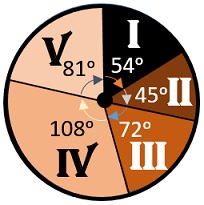
Aşağıdaki daire grafiklerindeki dilimlerden her birinin bütünün yüzde kaçına denk geldiğini bulalım.
