SÜRE
40:002015-2016 TEOG 2. DÖNEM MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2015-2016 TEOG 2. DÖNEM
SÜRE
40:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
... sayısı aşağıdakilerden hangisine eşittir?
... ... ... ...
CEVAP: C
... ve ... birer rakamdır.
... bir rasyonel sayı olduğuna göre ... aşağıdakilerden hangisi olamaz?
... ...
Bu sayının rasyonel olabilmesi için ...'nin tam kare olması gerekir. Buna göre ... sayısı 00, 01, 04, 09, 16, 25, 36, 49, 64 veya 81 olabilir. Bu sayılardan hiçbirinin onlar basamağındaki rakam 5 olmadığı için ... rakamı 5 olamaz.
CEVAP: A
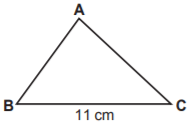
Şekildeki ABC üçgeninin çevresi santimetre cinsinden bir tam sayı ve |BC| = 11 cm’dir.
Buna göre ABC üçgeninin çevresi en az kaç santimetredir?
ABC üçgeninin çevresi, kenar uzunluklarının toplamıdır.
Çevre = |AB| + |AC| + 11
Bir üçgende iki kenar uzunluğunun toplamı, üçüncü kenar uzunluğundan fazla olmalıdır. Buna göre |AB| + |AC| uzunluğu, 11 cm’den büyüktür. Santimetre cinsinden çevre bir tam sayı olduğuna göre, |AB| + |AC|’nin alabileceği en küçük değer 12 cm’dir. Dolayısıyla, üçgenin çevresi en az 11 + 12 = 23 cm'dir.
CEVAP: D
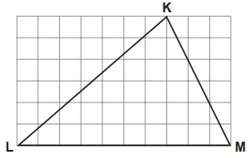
Kareli zeminde verilen KLM üçgeninde [LM] kenarına ait kenarortayın ve yüksekliğin [LM] kenarını kestiği noktalar arasındaki uzaklık 12 cm'dir.
Buna göre |LM| kaç santimetredir?

[LM] kenarına ait yüksekliğin ve kenarortayın bu kenarı kestiği noktalar arasındaki uzaklık 2 birimdir. 2 birim 12 cm'ye eşitse, 1 birim 6 cm'dir. Buna göre, 10 birimlik |LM| uzunluğu 10 × 6 cm = 60 cm'dir.
CEVAP: B
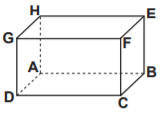

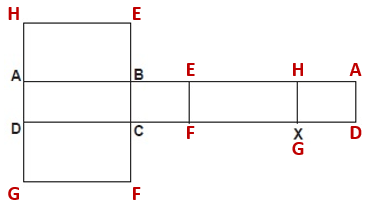
Yukarıdaki şekilde bir dikdörtgenler prizması ve bu prizmanın açınımı verilmiştir.
Buna göre açınımındaki X noktası dikdörtgenler prizmasının hangi köşesidir?
Ön yüzdeki ayrıtları D-C doğrultusunda takip ettiğimizde sırasıyla D-C-F-G-D noktalarının gelmesi gerektiğini görebiliriz. Buna göre, X noktasına karşılık gelen nokta G'dir.
CEVAP: A
DEF üçgeninin çevresinin ABC üçgeninin çevresine oranı ...'tür.
... ve |BC| = 24 cm olduğuna göre |EF| kaç santimetredir?
Benzer üçgenlerde çevrelerin oranı, benzerlik oranı ile aynıdır. Buna göre |EF|'nin |BC|'ye oranı ...'e eşittir.
...
⇒ ... cm
CEVAP: B
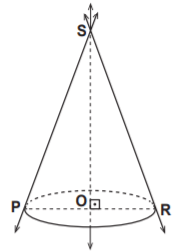
Şekilde verilen dik koni ile ilgili;
ifadelerinden hangileri doğrudur?
CEVAP: C
Tabanı düzgün çokgen olan bir piramidin 7 köşesi vardır. Bu piramidin yan yüzlerinin alanları toplamı 120 cm2 ve tabanının çevresi 24 cm'dir.
Buna göre bu piramidin yan yüz yüksekliği kaç santimetredir?
Piramidin 7 köşesi olduğuna göre tabanı düzgün altıgendir. Bu nedenle birbirine eş 6 yan yüzü vardır. Toplam alanı 120 cm2 olduğuna göre yan yüzlerden birinin alanı 120 ÷ 6 = 20 cm2'dir.

Taban çevresi 24 cm ise yan yüzü oluşturan üçgenin tabanı 24 ÷ 6 = 4 cm'dir.
Tabanı 4 cm ve alanı 20 cm2 olan üçgenin yüksekliği 10 cm'dir.
CEVAP: D
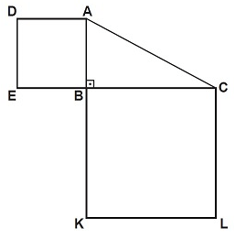
Şekildeki EBAD ve KLCB karelerinin alanları sırasıyla 64 cm2 ve 225 cm2 dir.
[EC] ... [AK] olduğuna göre |AC| kaç santimetredir?
EBAD karesinin kenar uzunluğu ... cm ve KLCB karesinin kenar uzunluğu ... cm'dir. Buna göre, |AB| = 8 cm ve |BC| = 15 cm’dir. Soruda uzunluğu istenilen AC kenarı, ABC dik üçgeninin hipotenüsüdür.

Hipotenüsü bulabilmek için Pisagor bağıntısını kullanırız.
|AC| ... ... ... ... cm
CEVAP: B
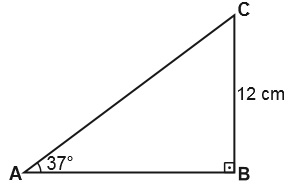
Şekildeki ABC üçgeninde [AB] ... [BC], ... ve |CB| = 12 cm olduğuna göre |AC| kaç santimetredir?
(cos53° = 0,6 kabul ediniz.)
... açısının ölçüsü ... ... ... 'dir.
|CB|'nin |AC|'ye oranı 53°'nin kosinüsüne eşittir. Buna göre,
...
⇒ ...
⇒ ...
⇒ ... 'dir.
CEVAP: C

96 birim küpten oluşan şekildeki dikdörtgenler prizmasının tüm yüzeyi boyanıyor.
En az bir yüzü boyalı birim küpler atıldıktan sonra geriye kaç tane birim küp kalır?
Bu dikdörtgenler prizmasının eni 8, boyu 4 ve derinliği 3 küp uzunluğundadır. En dıştaki boyalı küpleri çıkarırsak, tüm bu boyutlardan 2'şer küpü çıkarmamız gerekir. Geriye kalan dikdörtgenler prizmasının eni 8 – 2 = 6, boyu 4 – 2 = 2 ve deriniği 3 – 2 = 1 küp uzunluğunda olur. Bu sayıları çarparak geriye kaç küp kaldığını bulabiliriz.
6 × 2 × 1 = 12
CEVAP: B
Üç kutunun her birinde aynı özelliğe sahip, 1 ve 2 sayılarının yazılı olduğu ikişer kart vardır.
Bu kutuların her birinden rastgele birer kart alındığında, alınan bu kartların üzerinde yazılı olan sayıların toplamının 5 olma olasılığı kaçtır?
Karşımıza çıkabilecek sonuçları sıralı üçlülerle ifade edelim. Örneğin, (1, 2, 2) gösterimi ilk kutudan 1, ikinci ve üçüncü kutulardan 2 rakamının çekildiğini göstersin.
Üç kutunun her birinde iki çeşit rakam olduğu için karşımıza 2 × 2 × 2 = 8 farklı durum çıkabilir. Bu durumlardan (1, 2, 2), (2, 1, 2) ve (2, 2, 1) için rakamların toplamı 5 yapar. 8 durumdan 3'ü bu şartı sağladığı için aradığımız olasılık ...'dir.
CEVAP: B

Yukarıda verilen k ve m doğruları paraleldir. k doğrusu üzerinde A, B, C noktaları ve m doğrusu üzerinde D, E, F, G, H noktaları bulunmaktadır.
Buna göre köşeleri bu sekiz noktadan dördü olacak şekilde kaç farklı dörtgen çizilebilir?
Çizilecek şeklin bir dörtgen olabilmesi için köşe noktalarından ikisi k ve diğer ikisi l doğrusunun üzerinde olmalıdır.
Bu iki olay bağımsız olduğu için toplam 3 × 10 = 30 farklı dörtgen çizilebilir.
CEVAP: A
Aşağıdakilerden hangisi x2 + 6y – xy – 6x ifadesinin çarpanlarından biridir?
Verilen ifadede
alalım.
x2 + 6y – xy – 6x = x2 – xy – 6x + 6y
= x(x – y) – 6(x – y)
= (x – 6)(x – y)
Soruda verilen ifadenin çarpanları x – 6 ve x – y'dir.
CEVAP: D

Koordinat düzleminde 1. konumdaki şeklin 2. konuma geçişi aşağıda verilen hangi iki hareket sonucu oluşmuş olabilir?
1. konumdaki şekiller 8 birim sağa ötelendiğinde, 2. konumdaki şekillerin x eksenine göre yansıması elde edilir. Bu nedenle cevap B seçeneğidir.
CEVAP: B
... cebirsel ifadesi aşağıdakilerden hangisine eşittir?
... ... ...
Pay ve paydadaki ...'ler birbirini götürdüğünde sonuç ... çıkar.
CEVAP: C

Yukarıdaki koordinat düzleminde verilen hangi iki noktadan geçen doğrunun eğimi ...'dir?
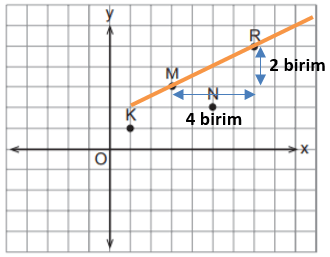
Aradığımız noktaların y-koordinatları arasındaki fark, x-koordinatları arasındaki farkın yarısına eşit olmalıdır. Ayrıca eğim pozitif olduğu için bu noktalardan geçen doğru sağ tarafa eğimli olmalıdır. R ve M noktalarından geçen doğru bu şartlara uyduğu için cevap A'dır.
CEVAP: A
... ... denklemini sağlayan ... sayısı kaçtır?
Bu denklemde, x'li terimleri sol tarafta ve sabit terimleri sağ tarafta toplayalım.
Sağdaki ...'yi sola ve soldaki ...'ü sağa geçirirsek, denklem
... ...
haline dönüşür. Eşitliğin solundaki işlemin sonucu ...'e ve sağındaki işlemin sonucu ...'e eşittir.
...
CEVAP: D

Doğrusal bir yol boyunca şekildeki gibi 6 tane fidan dikilmiştir. Bu fidanlar arasındaki ilk üç aralığın her biri x metre, son iki aralığın her biri y metredir.
x sayısı, y sayısından 2 fazla ve 2. fidan ile 5. fidan arasındaki aralıkların uzunlukları toplamı 22 metre olduğuna göre x sayısı kaçtır?
x sayısı, y sayısından 2 fazla ise x = y + 2'dir.
2. ve 5. fidanlar arasındaki uzaklık 22 metre ise, 2x + y = 22'dir.
Bulduğumuz denklemlerde, değişkenleri eşitliğin soluna sabit sayıları eşitliğin sağına yazarsak, aşağıdaki denklem sistemini elde ederiz.
x – y = 2
2x + y = 22
Bu denklem sistemini çözebilmek için denklemleri taraf tarafa toplayabiliriz.
x – y + 2x + y = 2 + 22
⇒ 3x = 24
⇒ x = 8
CEVAP: D
Bozuk bir baskül üzerindeki bir kütleyi gerçek kütlesinden 2 kilograma kadar daha fazla veya 5 kilograma kadar daha az gösterebilmektedir. Bu baskülün 70 kilogram gösterdiği bir kişinin gerçek kütlesi x kilogramdır.
Buna göre x'in değer alabileceği en geniş aralık aşağıdaki eşitsizliklerin hangisinde verilmiştir?
Kişinin gerçek kütlesi x kilogramsa, baskülün gösterdiği değer en fazla x + 2 kilogram olabilir. Bu ilişkiyi matematiksel olarak aşağıdaki gibi gösterebiliriz.
70 ≤ x + 2
Sağ taraftaki 2'yi sola attığımızda, x'in 68'den büyük veya 68'e eşit olduğunu görebiliriz.
5 kilograma kadar daha az gösterdiği için baskülde gördüğümüz değer en az x – 5 kilogram olabilir.
70 ≥ x – 5
Sağdaki –5'i sola attığımızda, x'in 75'ten küçük veya 75'e eşit olduğunu görebiliriz.
Yukarıdaki eşitsizlikleri birleştirdiğimizde C seçeneğindeki sonucu elde ederiz.
CEVAP: C