SÜRE
40:002016-2017 TEOG 2. DÖNEM (MAZERET) MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2016-2017 TEOG 2. DÖNEM-MAZERET
SÜRE
40:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
18 tane 9'un çarpımının, 3 tane 3'ün toplamına bölümü aşağıdakilerden hangisidir?
Bölme işleminin sonucu ise,
......'dir.
CEVAP: B
Aşağıdakilerden hangisi –9x . x cebirsel ifadesine özdeş değildir?
–9x . x =
A) –3x . 3x =
B) 9x . (–x) =
C) –x . (–9x) =
D) –3 . 3x2 =
CEVAP: C
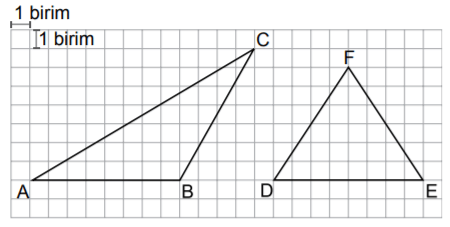
Yukarıdaki kareli zeminde verilen ABC üçgeninde, AB kenarına ait yükseklik ile DEF üçgenindeki F açısına ait açıortayın uzunlukları toplamı kaç birimdir?
DEF üçgeninde DE kenarına bir dik indirdiğimizde, bu doğru parçasının DE'yi 2 eşit parçaya böldüğünü görebiliriz. Bu da bize DEF üçgeninde yüksekliğin aynı zamanda kenarortay olduğunu gösterir. Buradan DEF'nin ikizkenar olduğunu çıkarabiliriz. Bu üçgende DE kenarına ait yükseklik aynı zamanda F açısına ait açıortaydır.
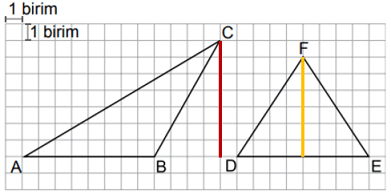
Yukarıda ABC üçgeninde AB kenarına ait yüksekliği kırmızı ve DEF üçgeninde DE kenarına ait yüksekliği sarı doğru parçaları ile gösteriyoruz. Kırmızı doğru parçası 7 birim ve sarı doğru parçası 6 birim olduğu için toplam uzunluk 7 + 6 = 13 birimdir.
CEVAP: A
...... işleminin sonucu bir tam sayıdır.
Buna göre A sayısı aşağıdakilerden hangisi olabilir?
Yukarıdaki sonuçları işlemde yerlerine koyarsak ... ifadesini elde ederiz. Sonucun tam sayı olabilmesi için köklü ifadeden kurtulmamız gerekir. B seçeneğinde verilen sayı, işlemdeki kareköklü ifadenin toplamaya göre tersi olduğu için A yerine bu sayıyı yazabiliriz.
......
CEVAP: B
Kız ve erkek öğrencilerin bulunduğu 30 kişilik bir sınıftan rastgele seçilen bir öğrencinin kız olma olasılığı erkek olma olasılığından daha fazladır.
Buna göre bu sınıfta en az kaç kız öğrenci vardır?
Seçilen öğrencinin kız olma olasılığı daha fazla ise bu sınıftaki kız öğrencilerin sayısı erkek öğrencilerden fazladır. Buna göre, sınıfta en az 16 kız öğrenci vardır.
CEVAP: C

Verilen koordinat düzleminde P, R, S, T noktaları işaretlenmiştir.
Buna göre aşağıdaki hangi iki noktadan geçen doğrunun eğimi ... olur?
Bu doğru üzerindeki iki noktanın y-koordinatları arasındaki fark, x-koordinatları arasındaki farkın ...'ü kadardır. Ayrıca ... pozitif bir sayı olduğu için aradığımız doğru sağ tarafa eğimlidir.

Bu şartlara uyan noktalar D seçeneğinde verilmiştir.
CEVAP: D
...... olduğuna göre ... kaçtır?
x'li terimleri sol tarafta ve sabit terimleri sağ tarafta toplayalım.
......
Sabit terimler arasındaki işlemin sonucu 5 – 1 = 4'tür. Sol taraftaki ifadeyi sadeleştirebilmek için paydaları eşitler çıkarma işlemini yaparız.
......
⇒ ...
x'in değerini bulabilmek için her iki tarafı da 4'le çarparız.
...
⇒ ...
CEVAP: A
Uç noktaları A ve B olan 60 cm uzunluğundaki bir tel iki noktasından bükülüp A ve B noktaları çakıştırılarak, kenar uzunlukları santimetre cinsinden birer tam sayı olacak şekilde bir üçgen oluşturulacaktır.
Aşağıdakilerden hangisi bu üçgenin kenarlarından birinin santimetre cinsinden uzunluğu olamaz?
Telin toplam uzunluğu 60 cm olduğu için oluşturduğumuz üçgenin çevresi de 60 cm'dir.
Kenar uzunluklarından biri 30 cm olsaydı, diğer iki kenar uzunluğunun toplamı da 60 – 30 = 30 cm olurdu. Fakat bir üçgende iki kenar uzunluğunun toplamı, üçüncü kenar uzunluğundan fazla olmalıdır. Bu kurala uymadığı için sorudaki üçgenin kenar uzunluklarından biri 30 cm olamaz.
CEVAP: D
Bir torbada renkleri dışında aynı özelliklere sahip mavi ve kırmızı toplar bulunmaktadır.
Torbadan rastgele çekilen bir topun kırmızı olma olasılığı aşağıdakilerden hangisi olamaz?
Olasılık 0'dan küçük veya 1'den büyük olamaz. B seçeneğindeki sayı 1'den büyük olduğu için çekilen topun kırmızı olma olasılığı bu değere eşit olamaz.
CEVAP: B

ABC ikizkenar üçgeninde |AB| = |AC| ve [AD] ... [BC]'tir.
|BC| = 16 cm ve |AB| = 17 cm olduğuna göre |AD| kaç santimetredir?
|AB| = |AC| olduğu için [AD] yalnızca yükseklik değil aynı zamanda kenarortaydır ve [BC] kenarını iki eşit parçaya böler. Bu nedenle |BD| = 8 cm'dir. ABD dik üçgeninde Pisagor bağıntısını kullanarak |AD| uzunluğunu elde edebiliriz.
|AB|2 = |BD|2 + |AD|2
⇒ 172 = 82 + |AD|2
⇒ 289 = 64 + |AD|2
⇒ 225 = |AD|2
⇒ |AD| = 15 cm
CEVAP: B
Aşağıdakilerden hangisi ab + a + bc + c cebirsel ifadesine özdeştir?
Seçeneklerdeki parantezleri açıp hangi seçeneğin soruda verilen ifadeye eşit olduğunu bulalım.
A) (a + b)(c + 1) =
B) c . (a + b) =
C) (a + c)(b + 1) =
D) a . (b + c) =
CEVAP: C

Aşağıdaki noktalardan hangisi şekildeki ABCD dörtgeninin x eksenine göre yansıması olan dörtgenin içinde yer alır?
ABCD dörtgeninin x-eksenine göre yansıması aşağıdaki şekilde

Seçeneklerdeki noktalar farklı renklerle gösterilmiştir.
Sarı nokta,
CEVAP: B

2x + y – 4 = 0 denkleminin belirttiği grafik yukarıda verilmiştir.
Buna göre a + b kaçtır?
a sayısı, 2x + y – 4 = 0 denkleminde x yerine 0 yazıldığında y'nin aldığı değere eşittir.
2 . 0 + y – 4 = 0
⇒ y = 4
b sayısı ise, aynı denklemde y yerine 0 yazıldığında x'in aldığı değere eşittir.
2x + 0 – 4 = 0
⇒ x = 2
a = 4 ve b = 2 olduğu için a + b toplamı 6'ya eşittir.
CEVAP: C
Denklemleri y = 3 ve y = x olan doğruların kesim noktasının koordinatları aşağıdakilerden hangisidir?
y = 3 doğrusu üzerindeki tüm noktaların y-koordinatı 3'tür. y = x doğrusunda y yerine 3 yazdığımızda x'in değeri de 3 çıkar. Buna göre, verilen doğruların kesişim noktasının koordinatları (3, 3)'tür.
CEVAP: D

Şekilde verilen ABCD dikdörtgeninin alanını santimetre cinsinden gösteren cebirsel ifade aşağıdakilerden hangisidir?
Dikdörtgenin alanını bulabilmek için kenar uzunluklarını çarparız. Bu dikdörtgenin kenar uzunlukları x ve y + 2 olduğu için bu iki ifadeyi çarparak sonuca ulaşabiliriz.
x . (y + 2) = xy + 2x
CEVAP: B
–3 . (x + 7) ≥ 6 eşitsizliğinin çözümü aşağıdakilerden hangisidir?
Bu eşitsizliği çözebilmek için soldaki –3'ü karşı tarafa atarız. Bu sayı negatif olduğu için eşitsizliğin yönünü de değiştiririz.
x + 7 ≤ –2
Soldaki x'i yalnız bırakabilmek için 7'yi sağ tarafa atarız.
x ≤ –2 – 7
Böylece C seçeneğinde verilen eşitsizliğin doğru olduğunu görebiliriz.
x ≤ –9
CEVAP: C
Kenar uzunlukları 6 santimetre, 9 santimetre ve 4 santimetre olan bir üçgen ile kenar uzunlukları 12 santimetre, 18 santimetre ve 27 santimetre olan üçgen benzerdir.
Bu iki üçgen arasındaki benzerlik oranı aşağıdakilerden hangisi olabilir?
Bu üçgenlerin en kısa kenar uzunluklarını oranlayarak benzerlik oranının
...
olduğunu görebiliriz.
CEVAP: A
... sayısının aşağıdakilerden hangisi ile çarpımı bir irrasyonel sayıdır?
... bir doğal sayıdır. Bu sayı, ancak irrasyonel bir sayıyla çarpıldığında sonuç irrasyonel olur.
A, B ve C seçeneğinde verilen sayılar rasyonel olduğu için 15 ile çarpımları da rasyoneldir.
D seçeneğinde verilen sayı irrasyonel olduğu için bu sayının 15'le çarpımı da irrasyoneldir.
...
CEVAP: D
4x – 5y = 17
2x + 7y = –1
denklem sisteminin çözümü aşağıdakilerden hangisidir?
İkinci denklemi –2 ile çarptığımızda denklem sistemi
4x – 5y = 17
–4x – 14y = 2
haline dönüşür. Bu denklemleri taraf tarafa topladığımızda
4x – 5y – 4x – 14y = 17 + 2
⇒ –19y = 19
⇒ y = –1
sonucu çıkar. İlk denklemde y yerine –1 yazdığımızda,
4x –5(–1) = 17
⇒ 4x + 5 = 17
⇒ 4x = 12
⇒ x = 3
sonucunu elde ederiz. Buna göre, denklem sisteminin çözümü (3, –1) noktasıdır.
CEVAP: A

Kareli zeminde verilen AB doğru parçası O noktası etrafında döndürülerek A'B' doğru parçası elde edilmiştir.
Buna göre AB doğru parçasına aşağıdaki dönme hareketlerinden hangisi uygulanmıştır?
O noktasını orijin, bu noktadan geçen yatay doğruyu x ekseni ve dikey doğruyu y ekseni olarak kabul edersek, B noktasının koordinatları (–4, 3) ve B' noktasının koordinatları (–3, –4) olur. Bu hareket saat yönünün tersine 90° veya saat yönünde 270° dönme hareketidir.

CEVAP: B