SÜRE
40:002018-2019 LGS MATEMATİK
ÇÖZÜMLÜ DENEME OLARAK ÇÖZ

Sınıf 8 ➤ DENEME OLARAK ÇÖZ ➤ 2018-2019 LGS
SÜRE
40:00
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
Bir otelin her bir katındaki oda sayısının, odaların bulunduğu katın numarasına göre değişimini gösteren tablo aşağıda verilmiştir.
Tablo: Kat Numarasına Göre Kattaki Oda Sayısı
| Kat Numarası (x) | Kattaki Oda Sayısı |
| 1 ≤ x < 4 | 90 – 10x |
| 4 ≤ x < 7 | 50 – 5x |
Buna göre bu otelde 2. kattaki oda sayısı 5. kattaki oda sayısından kaç fazladır?
Çözüm:
2. Kattaki Oda Sayısı
| Kat Numarası (x) | Kattaki Oda Sayısı |
| 1 ≤ x < 4 | 90 – 10x |
| 4 ≤ x < 7 | 50 – 5x |
x = 2 için ilk satırdaki cebirsel ifadeyi kullanırız. 90 – 10x ifadesinde x yerine 2 yazarak, 2. katta 70 oda olduğunu görebiliriz.
90 – 10x = 90 – 10 . 2 = 90 – 20 = 70 oda
5. Kattaki Oda Sayısı
| Kat Numarası (x) | Kattaki Oda Sayısı |
| 1 ≤ x < 4 | 90 – 10x |
| 4 ≤ x < 7 | 50 – 5x |
x = 5 için ikinci satırdaki ifadeyi kullanırız. Bu ifadede x yerine 5 yazarak 5.katta kaç oda olduğunu bulabiliriz.
50 – 5x = 50 – 5 . 5 = 50 – 25 = 25 oda
Aradaki Fark
2. katta 70 ve 5. katta 25 oda vardır. Oda sayıları arasındaki fark 70 – 25 = 45'tir.
CEVAP: B
...,... ve ... birer gerçek sayı ve ... ≥ 0 olmak üzere
...
... ...
... ...
Aşağıdaki şekildeki gibi bir vincin havada tuttuğu inşaat malzemesinin yerden yüksekliği ... m ve malzemenin vincin koluna uzaklığı ... mʼdir.
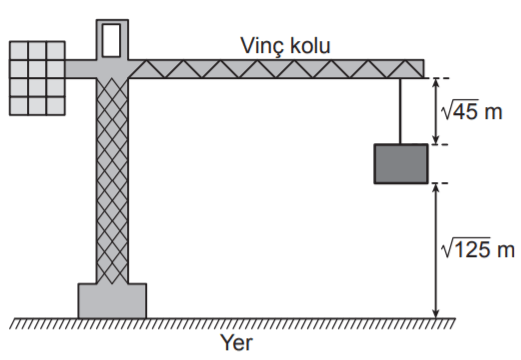
Vincin kolunun yerden yüksekliği sabit kalmak üzere malzeme şekildeki konumdayken... m yukarı çekiliyor.
Buna göre son durumda malzemenin yerden yüksekliği, malzemenin vincin koluna uzaklığından kaç metre fazladır?
Soruda verilen uzaklıkları kök dışına çıkaralım.
Malzeme ... m yukarı çekilirse, yeni uzaklıklar aşağıdaki gibi olur.
Buna göre, uzaklıklar arasındaki yeni fark ... ... m olur.
CEVAP: C
Bir ondalık gösterimin, basamak değerleri toplamı şeklinde yazılmasına ondalık gösterimin çözümlenmesi denir.
Uçakla seyahat eden bir yolcu, kütlesi 8 kg’dan az olan valizini kabine alabilmektedir.
Aycan’ın valizinin kütlesi 9,08 kg’dır. Bu valizdeki bazı eşyaların kütlelerinin çözümlenmiş şekli aşağıdaki tabloda verilmiştir.
Tablo: Valizdeki Eşyalardan Bazılarının Kütleleri
| Eşya | Kütlesi (kg) |
| Ayakkabı | 9 . 10–1 + 8 . 10–2 |
| Kitap | 1 . 100 + 1 . 10–1 |
| Mont | 9 . 10–1 + 5 . 10–3 |
| Tablet | 1 . 100 + 9 . 10–3 |
Aycan, valizinden bu dört eşyadan hangisini çıkarırsa valizini kabine alabilir?
Çözümlemesi yapılan eşyaların kütlelerini bulalım.
Aycan'ın valizinden çıkarması gereken kütle en az 9,08 – 8 = 1,08 kg olmalıdır. Seçeneklerde kütlesi 1,08 kg'dan fazla olan tek eşya kitaptır.
CEVAP: C
Aşağıda dikdörtgen şeklindeki A, B, C kartonlarının her birinden dörder adet verilmiştir.
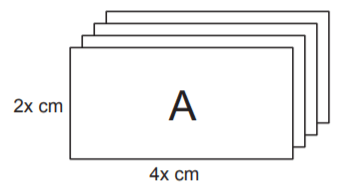


Bu kartonların kenarları çakıştırılarak iki tane kare prizma oluşturuluyor. Bu prizmalardan biri aşağıda verilmiştir.
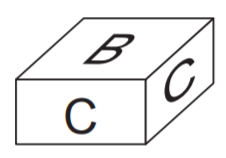
Kartonların tamamı kullanıldığına göre diğer prizmanın yüzey alanı kaç santimetrekaredir?
İlk kare prizma için 2 tane B ve 4 tane C kartonu kullanılıyor. Buna göre ikinci kare prizma için geriye 2 tane B ve 4 tane A kartonu kalıyor.

A kartonunun yüzey alanı 2x . 4x = 8x2 cm2 ve B kartonunun yüzey alanı 2x . 2x = 4x2 cm2'dir. Buna göre, ikinci kare prizma için kullanılan kartonların toplam alanı
4 . 8x2 + 2 . 4x2 = 40x2 cm2'dir.
Bu alan, aynı zamanda, ikinci kare prizmanın yüzey alanına eşittir.
CEVAP: D
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı, hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
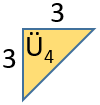
Geometri tahtası, bir zeminin üzerine eşit aralıklarla yerleştirilmiş çivilerden oluşur.
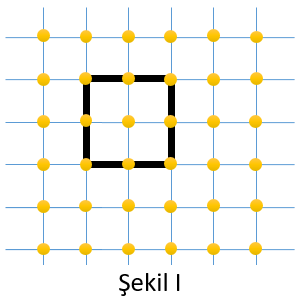

Şekil I’deki geometri tahtasında oluşturulan karenin alanı ...... birimkaredir.
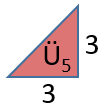
Bu geometri tahtasında Şekil II’deki gibi oluşturulan üçgenin çevre uzunluğu x cinsinden kaç birimdir?
Şekil I'de geometri tahtasında oluşturulan karenin alanı ... ... ... birimkaredir. Buna göre, karenin kenar uzunluğu ... ... birimdir.
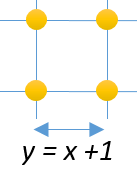
İki komşu çivi arasındaki uzaklığa ... dersek, karenin kenar uzunluğu... olur. Bu uzunluk ...'ye eşit olduğu için ... ... birimdir.
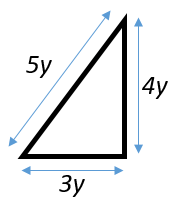
Şekil II'deki üçgenin dik kenar uzunlukları ... ve ... birimdir. Pisagor Teoremi'ni kullanarak, hipotenüs uzunluğunun ... olduğunu görebiliriz.
... ...... ...
Üçgenin çevresi kenar uzunluklarının toplamına eşittir.
Üçgenin Çevresi=... ...
... ifadesinde ... yerine ... yazdığımızda, sonucun ... birim olduğunu görebiliriz.
... ......
CEVAP: A
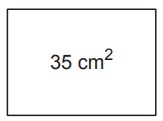


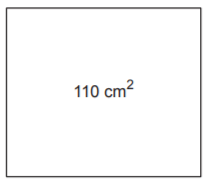
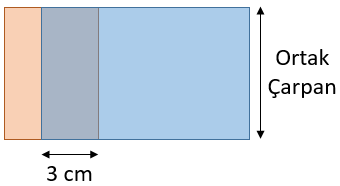
Kenarlarının uzunlukları santimetre cinsinden 1ʼden büyük tam sayı olan dikdörtgen şeklindeki kartonlar ve bu kartonların bir yüzlerinin alanları yukarıda verilmiştir. Bu kartonlardan yüzey alanları farklı olan ikisi seçilip 3 cmʼlik kısımları üst üste yapıştırılarak aşağıdaki gibi bir dikdörtgen karton oluşturulacaktır.

Bu şekilde oluşturulan kartonun bir yüzünün alanı en fazla kaç santimetrekaredir?
Bu kartonlara küçükten büyüğe doğru (soldan sağa doğru) sırayla
Soruda verilenlere göre, bir kartonun kenar uzunlukları alanının 1'den büyük çarpanlarıdır. Kartonlara ait kenar uzunluklarının santimetre cinsinden alabileceği değerleri gösteren sayı ikilileri aşağıdaki gibidir.
İki farklı karton, şekildeki gibi üst üste yapıştırılacaksa, bu kartonların kenar uzunluklarından biri aynı olmalıdır. Buna göre, olası çözümleri bulabilmek için yukarıdaki ikililerden ortak olanları seçmemiz gerekir. Ortak uzunluğa sahip olabilecek kartonlar ve bu kartonlar yapıştırıldığında oluşan şekillerin alanları aşağıdaki gibidir.
Ortak Uzunluk: 7 cm
Alan=7 × (11 + 5 – 3) = 91 cm2
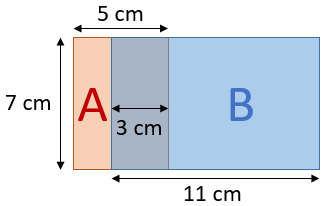
Ortak Uzunluk: 5 cm
Alan=5 × (7 + 22 – 3) = 130 cm2

Ortak Uzunluk: 11 cm
Alan=11 × (7 + 10 – 3) = 154 cm2

Olası alanlardan en büyüğü 154 cm2'dir.
CEVAP: C

Yukarıdaki kareli zeminde verilen şekilde A, B, C noktaları sırasıyla D, E, F noktalarıyla birleştirilerek [AD], [BE] ve [CF] çiziliyor.
Buna göre aşağıdakilerden hangisi elde edilen üçgenlerden benzer olan herhangi ikisinin benzerlik oranı olamaz?
Soruda belirtilen doğruları çizelim.

Bu doğruları çizdiğimizde, karşımıza 6 farklı dik üçgen çıkar.
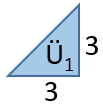

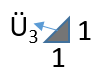

Benzerlik oranı ... olan benzer üçgenler bulunmamaktadır.
CEVAP: B
..., ... birer gerçek sayı ve ... ≥ ... olmak üzere ... dir.
Dikdörtgen şeklindeki bir kâğıt aşağıdaki gibi kesilerek kare ve dikdörtgen şeklinde iki kâğıt elde ediliyor. Elde edilen kare şeklindeki kâğıdın bir yüzünün alanı 27 cm2 olup dikdörtgen şeklindeki kâğıdın bir yüzünün alanının 3 katına eşittir.

Buna göre elde edilen dikdörtgen şeklindeki kâğıdın kısa kenarının uzunluğu kaç santimetredir?
Karenin kenar uzunluğu ... ... cm'dir.
Dikdörtgenin uzun kenarı, karenin üst kenarı ile ortak olduğu için bu uzunluk da ... cm'dir. Ayrıca soruda verilenlere göre dikdörtgenin alanı 27 ÷ 3 = 9 cm2'dir.
Alanı 9 cm2 ve uzun kenarı ... cm olan dikdörtgenin kısa kenarı ... cm'dir.
... cm
CEVAP: D
Eğim, dikey uzunluğun yatay uzunluğa oranıdır.
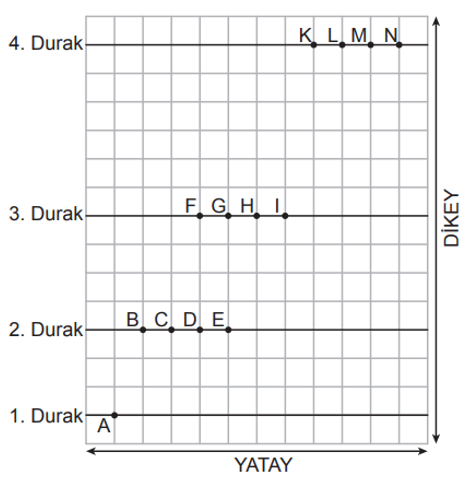
Yukarıdaki kareli zeminde verilen A noktasından yola çıkan bir hareketli, eğimi 1 olan yolu izleyerek 2. duraktaki noktalardan birine ulaştıktan sonra bu noktadan eğimi 2 olan yolu izleyerek 3. duraktaki noktalardan birine ulaşıyor.
Ardışık iki durak arasında izlediği yollar doğrusal olduğuna göre bu hareketli,3. durakta bulunduğu noktadan eğimi 3 olan yolu izleyerek 4. duraktaki hangi noktaya ulaşır?
Bu hareketlinin izlediği yollar aşağıda gösterilmiştir.

CEVAP: A
Gülle atma yarışmalarında her bir sporcunun üç atış yapma hakkı vardır. Bu üç atıştan sonra sporcular, gülleyi attıkları en uzun mesafeye göre büyükten küçüğe doğru sıralanır. Bu sıralama sonucunda sporculardan birinci sıradaki altın, ikinci sıradaki gümüş, üçüncü sıradaki bronz madalya alır.
Aşağıdaki tabloda beş sporcunun katıldığı bir gülle atma yarışmasında bu sporcuların atış mesafeleri verilmiştir.
Tablo: Sporcuların Gülle Atış Mesafeleri (Metre)

Bu yarışmada Cihan altın madalya, Dinçer bronz madalya kazandığına göre Fatih’in 3. atışında gülleyi attığı mesafenin metre cinsinden alabileceği değerler aşağıdaki sayı doğrularının hangisinde gösterilmiştir?
Madalya sıralamalarında sadece en iyi atışlar değerlendirilmektedir. Burak, Cihan, Dinçer ve Erdal'ın madalya sıralamalarında kullanılan atışları aşağıdaki gibidir.
Bu atışlardan en iyisi Cihan'ınkidir ve Cihan altın madalya almıştır. Fatih'inkiler hariç, en iyi ikinci atış ise Dinçer'indir. Dinçer bronz madalya aldığına göre, gümüş madalyayı Fatih almıştır. Buna göre, Fatih'in en iyi atışının, Cihan'ın en iyi atışıyla, Dinçer'in en iyi atışı arasında olması gerekir. Metre cinsinden Fatih'in en iyi atışına x dersek, bu değişken aşağıdaki eşitsizliği sağlar.
18,57 < x < 19,86
Bu eşitsizliğin sayı doğrusunda gösterimi, D seçeneğinde verilmiştir.
Not: Fatih'in diğer iki atışı 18,57'den küçük olduğu için bu atışlar sonucu değiştirmez.
CEVAP: D
Eşit uzunluktaki iki çubuğun birinden 8 cmʼlik bir parça kesilerek kalan kısım iki eş parçaya, diğerinden 5 cmʼlik bir parça kesilerek kalan kısım üç eş parçaya aşağıdaki gibi ayrılıyor.

Bu parçalardan birer tanesi ile bir kitabın aynı kenarı aşağıdaki gibi ölçüldüğünde parçalardan birinin uzunluğu kitabın kenar uzunluğundan 10 cm fazla, diğerinin uzunluğu ise 1 cm eksik oluyor.

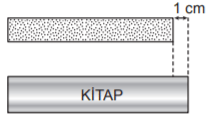
Buna göre kesilmeden önce çubuklardan birinin uzunluğu kaç santimetredir?
Çubukların uzunluklarını ... ile gösterip, parça uzunluklarını bu değişken cinsinden bulalım.
Üstteki çubuğun parçası:
Üstteki çubuğun 8 cm'si kesilince geriye ... cm'si kalır. Geriye kalan kısım ikiye bölününce, parçalardan her birinin boyu ... cm olur.
Alttaki çubuğun parçası
Alttaki çubuğun 5 cm'si kesilince geriye kalan kısım ... cm uzunluğunda olur. Bu kısım üçe bölününce, parçalardan her biri ... cm uzunluğunda olur.
Şimdi de yukarıda bulduğumuz ifadelerle bir denklem oluşturup, bu denklemi çözelim.
Denklem
Üstteki çubuğun bir parçası soruda verilen kitaptan 10 cm uzun ve alttaki çubuğun bir parçası aynı kitaptan 1 cm kısadır. Buna göre, ...'nin 10 eksiği, ...'ün 1 fazlasına eşittir.
......
Denklem Çözümü
Denklemdeki paydalardan kurtulabilmek için eşitliğin iki tarafını da 6 ile çarpabiliriz.
......
⇒ ............
⇒ ............
⇒ .........
⇒ ......
⇒ ......
⇒ ... cm
CEVAP: B

İçinde kırmızı veya sarı renkli 5 topun bulunduğu 1. torbadan rastgele çekilen bir topun kırmızı olma olasılığı daha fazladır. Ayrıca mavi veya sarı renkli 7 topun bulunduğu 2. torbadan rastgele çekilen bir topun sarı olma olasılığı daha azdır. 1. ve 2. torbadaki topların tamamı boş bir kutuya atılıp karıştırılıyor.
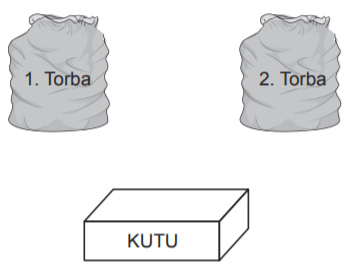
Topların tamamı renkleri dışında özdeş olduğuna göre bu kutudan rastgele çekilen bir topun sarı olma olasılığı en fazla kaçtır?
1. Torba:
1. torbadan rasgele çekilen bir topun kırmızı gelme olasılığı daha fazlaysa, sarı topların sayısı yarıdan azdır. Buna göre, ilk torbada en fazla 2 sarı top vardır.
2. Torba:
Bu torbadan rasgele çekilen bir topun sarı olma olasılığı daha düşükse, bu torbada da sarı topların sayısı tüm topların yarısından azdır. Buna göre ikinci torbada en fazla 3 sarı top vardır.
Kutu:
Torbalardaki toplar aynı kutuya atıldığında, bu kutuda toplam 5 + 7 = 12 top olur. 12 toptan en fazla 2 + 3 = 5'i sarıdır. Buna göre, kutudan çekilen topun sarı olma olasılığı en fazla ... olabilir.
CEVAP: C
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı, hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
ABCD dikdörtgeni biçimindeki bir kâğıt parçasının bir yüzüne aşağıdaki gibi 10 eş dikdörtgen çizilip bu dikdörtgenler boyanıyor.
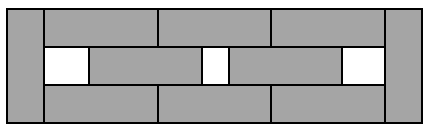
Kâğıdın bu yüzündeki boyanmayan bölgelerin alanları toplamı 30 cm2 olduğuna göre ABCD dikdörtgeninin köşegenlerinden birinin uzunluğu kaç santimetredir?
Boyasız alan:
Orta kısımdaki boyanmayan bölgelerin toplam alanı, eş dikdörtgenlerden birinin alanına eşittir. Bu durum, orta kısımdaki iki dikdörtgenin sola ve sağa yaslanmasıyla da görülebilir.

Eş dikdörtgenlerin kenar uzunlukları:

Eş dikdörtgenlerin kısa kenar uzunluğu ... ile ifade edildiğinde uzun kenar ... çıkar. Buna göre, boyasız bölgenin alanı ... cm2'dir. ... ifadesi 30'a eşitlenerek ...'in ...'a eşit olduğu görülebilir.
...
⇒ ...
⇒ ... cm
Kağıdın kenar uzunluğu:

Köşegen uzunluğu:
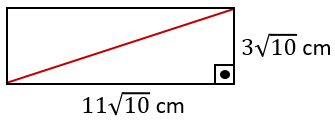
İki komşu kenar ve köşegen bir dik üçgen oluşturur. Bu dik üçgenin hipotenüsü, kağıdın köşegenidir. Köşegen uzunluğunun karesi Pisagor Teoremi'ne göre dik kenar uzunluklarının karelerinin toplamına eşittir.
...
...
... cm2
Buna göre köşegen uzunluğu ... cm'dir.
CEVAP: C
Yükseklikleri eşit olan dik dairesel silindir şeklindeki iki eş pakete kakaolu ve vanilyalı bisküviler, tabanları çakışacak şekilde aşağıdaki gibi tek sıra hâlinde yerleştiriliyor.

Kakaolu bir bisküvinin yüksekliği vanilyalı birbisküvinin yüksekliğinin yarısı kadardır. Paketlerden birine üç vanilyalı, iki kakaolu bisküvi konulduğunda paketin boş kalan kısmınınyüksekliği 10 cm; diğer pakete bir vanilyalıiki kakaolu bisküvi konulduğunda paketin boş kalan kısmının yüksekliği 14 cm oluyor.
Tam dolu bir paketteki vanilyalı bisküvi sayısı kakaolu bisküvi sayısına eşit olduğuna göre bu pakette kaç tane bisküvi vardır?
Kakaolu bisküvinin santimetre cinsinden yüksekliğine x dersek, vanilyalı bisküvinin yüksekliği 2x olur. Şimdi de paket yüksekliklerini x cinsinden bulalım.
Soldaki paketin yüksekliği
Soldaki paketin yüksekliği, 3 vanilyalı ve 2 kakaolu bisküvinin toplam yüksekliğinden 10 cm fazladır.
3 . 2x + 2 . x + 10 = 8x + 10 cm
Sağdaki paketin yüksekliği
Sağdaki paketin yüksekliği, 1 vanilyalı ve 2 kakaolu bisküvinin toplam yüksekliğinden 14 cm fazladır.
1 . 2x + 2 . x + 14 = 4x + 14 cm
Denklem
Paketlerin yükseklikleri eşit olduğu için 8x + 10 ile 4x + 14 ifadeleri eşittir.
8x + 10 = 4x + 14
⇒ 8x – 4x = 14 – 10
⇒ 4x = 4
⇒ x = 1 cm
Bisküvilerin ve paketin yükseklikleri
Tam dolu paketteki bisküvi sayısı
Bir vanilyalı ve bir kakaolu bisküvinin toplam yüksekliği 2 + 1 = 3 cm'dir. Vanilyalı ve kakaolu bisküviler eşit sayıda olacaksa, tam dolu pakette 18 ÷ 3 = 6 çift veya toplam 12 adet bisküvi olmalıdır.
CEVAP: B
Bir televizyon kanalında 24 saat boyunca yayımlanacak programların sürelerine göre dağılımı ve yayın sırası aşağıdaki daire grafiğinde gösterilmiştir. Bu daire grafiğine uygun 24 saatlik yayın akışını gösteren aşağıdaki gibi bir tablo oluşturulacaktır.
Grafik: Yayımlanacak Programların Sürelere Göre Dağılımı

Tablo: 24 Saatlik Yayın Akışı
| Sıra | Program Adı | Yayın Saati |
| 1 | El Emeği Göz Nuru | 08.00 - … |
| 2 | Başarının Sırrı | … - … |
| 3 | Anadolu’da Lezzet Durakları | … - … |
| 4 | Piramitlerin Gizemi | … - … |
| 5 | Çanakkale Destanı | … - … |
| 6 | Ata Sporlarımız | … - … |
| 7 | Doğanın Gücü | … - … |
| 8 | Dünya Atletizm Şampiyonası | … - … |
| 9 | Bilgisayar Dünyası | … - … |
| 10 | Notaların Dili | … - … |
Verilenlere göre “Ata Sporlarımız” adlı programın yayın saati aşağıdakilerden hangisidir?
24 saatlik zaman dilimi 360° ile ifade edildiğine göre bu dairedeki her 360° ÷ 24 = 15°'lik açı, bir saatlik bir dilimi göstermektedir.
"Ata Sporlarımız"dan önce başlayan 5 program, daire grafiğinde 30 + 15 + 45 + 15 + 60 = 165° ile gösterilmektedir. Buna göre, saat 8:00'dan "Ata Sporlarımız" programı başlayana kadar geçen süre 165 ÷ 15 = 11 saattir. 8:00'a 11 saat eklendiğinde 19:00 elde edilir. Bahsedilen program, daire grafiğinde 15° ile gösterildiği için program süresi 15 ÷ 15 = 1 saattir. Buna göre, "Ata Sporlarımız" programının yayın saati 19:00 ile 20:00 arasındadır.
CEVAP: A
..., ..., ..., ... birer gerçek sayı ve ... ≥..., ... ≥... olmak üzere
... ...
... dir.
... ...
... dir.

Tablo 1ʼde verilen ifadelerin her biri Tablo 2ʼde verilen ifadelerin her biri ile birer kez çarpılıyor. Bu şekilde elde edilen sayıların her biri, bir karta bir sayı gelecek şekilde özdeş kartlara yazılarak boş bir torbaya atılıyor.
Torbadan rastgele çekilen bir kartın üzerinde yazan sayının doğal sayı olma olasılığının ... olması için A yerine aşağıdakilerden hangisi yazılmalıdır?
Tablo 1 ve Tablo 2'deki sayıların mümkün olan tüm çarpanlarını kök dışına çıkaralım.

Bu tabloların her birinden birer sayı seçip çarptığımızda, sonucun doğal sayı olabilmesi için her iki sayının da kareköklü kısımlarının aynı olması gerekir. Tablo 1'deki ... ile Tablo 2'deki ... ve ... sayılarının çarpımı doğal sayıdır.
Tabloların her birinden birer sayı seçip çarparak 16 farklı sonuç elde edebiliriz. Bu sonuçlardan rasgele çekilen birinin doğal sayı olma olasılığının ...'e eşit çıkabilmesi için 16 sonuçtan 2'sinin doğal sayı olması gerekir. Yukarıda hâlihazırda 2 çarpımın doğal sayı olduğunu görmüştük. Bu nedenle, A'nın Tablo 2'deki herhangi bir sayı ile çarpımının doğal sayı olmaması gerekir. A sayısı ...'e eşit olduğunda, bu sayıyla yapılan çarpma işlemlerinin sonucu doğal sayı olmaz.
CEVAP: C
... ≠... ve ..., ... tam sayılar olmak üzere
... ve...
...
Aşağıda sadece ön yüzlerinde birer üslü ifadenin yazılı olduğu 4 mavi ve 4 kırmızı kart verilmiştir.
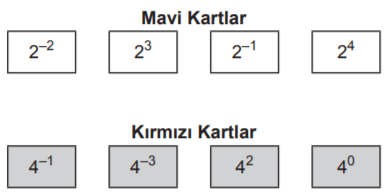
Mavi kartlardaki her bir üslü ifade kırmızı kartlardaki kendisine denk olmayan her bir üslü ifade ile birer kez çarpılarak yeni üslü ifadeler elde ediliyor.
Elde edilen bu üslü ifadelerden ikisinin birbirine oranı en çok kaçtır?
Kırmızı kartlardaki sayıları da 2 tabanında yazalım.
En büyük oranı yakalayabilmek için öncelikle çarpma sonucunda elde edilebilecek en küçük ve en büyük sayıları bulmamız gerekir.
En küçük çarpım:
Mavi ve kırmızı kartlardaki en küçük sayılar sırasıyla 2–2 ve 2–6'dır. Bu sayıların çarpımı elde edebileceğimiz en küçük sonucu verir.
2–2 . 2–6 = 2–2 – 6 = 2–8
En büyük çarpım:
Hem mavi hem de kırmızı kartlardaki en büyük sayı 24'tür. Yalnız denk olmayan üslü ifadeler çarpıldığı için 24'ü bu kartlardaki en büyük ikinci sayı ile çarpmamız gerekir. En büyük ikinci sayı 23 olduğundan, elde edilebilecek en büyük çarpım sonucu 24 . 23 = 27'dir.
En büyük oran:
En büyük oranı bulabilmek için en büyük çarpım sonucunu en küçük çarpım sonucuna böleriz.
... ...
CEVAP: B
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
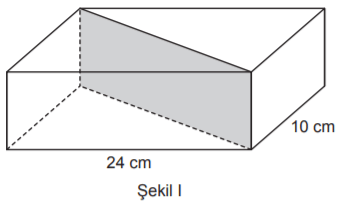
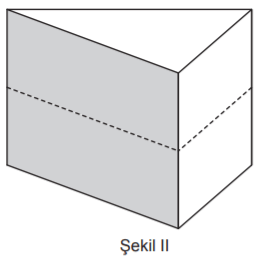
Taban ayrıtlarının uzunlukları 10 cm ve 24 cm olan dikdörtgenler prizması biçimindeki tahta blok Şekil I’deki gibi taban köşegenleri boyunca tabanlara dik olacak şekilde kesilerek iki eş parçaya ayrılıyor. Elde edilen iki parça üst üste yapıştırılarak Şekil II’deki dik üçgen dik prizma biçiminde bir tahta blok oluşturuluyor.
Elde edilen dik üçgen dik prizma ile başlangıçta verilen dikdörtgenler prizmasının ayrıtlarının uzunlukları toplamı birbirine eşittir.
Buna göre dikdörtgenler prizması şeklindeki tahta bloğun yüksekliği kaç santimetredir?
Dikdörtgenler Prizması:
Dikdörtgenler prizmasının yüksekliği x ile ifade edildiğinde, ayrıt uzunluklarının toplamı 4(24 + 10 + x) = 136 + 4x cm olur.
Dik Üçgen Dik Prizma:
Pisagor Teoremi kullanılarak, dikdörtgenler prizmasının taban köşegeninin 26 cm olduğu görülebilir.
......... cm
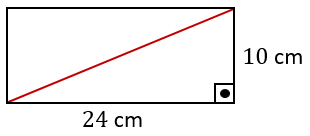
Buna göre, dik üçgen dik prizmanın ayrıt uzunluklarının toplamı 2(26 + 10 + 24) + 3 . 2x = 120 + 6x cm'dir.
Denklem:
x cinsinden bulunan ifadeler eşitlendiğinde aşağıdaki denklem elde edilir.
136 + 4x = 120 + 6x
⇒ 136 – 120 = 6x – 4x
⇒ 16 = 2x
⇒ x = 8 cm
Buna göre, dikdörtgenler prizmasının yüksekliği 8 cm'dir.
CEVAP: A
Braille alfabesi görme engellilerin okuyup yazmaları için geliştirilmiş bir yazı sistemidir. Braille rakamları da aşağıdaki gibi tanımlanmıştır.
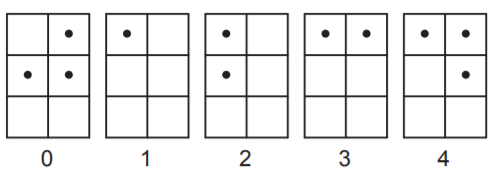

Bu rakamlar kullanılarak aşağıdaki gibi dört haneli bir şifre oluşturulacaktır.
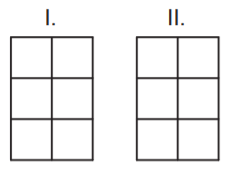
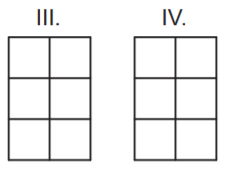
Bu dikdörtgenlerden I. ile II. ve III. ile IV. dikdörtgen aşağıdaki gibi uzun kenarları boyunca çakıştırıldıklarında bu dikdörtgenlerin belirttiği Braille rakamları çakışma kenarlarına göre birbirinin yansıması olacaktır.


Yukarıdaki gibi oluşturulacak bu şifrede I. ve II. dikdörtgenlerdeki Braille rakamlarından oluşan iki basamaklı sayı tam kare, III. ve IV. dikdörtgenlerdeki Braille rakamlarından oluşan iki basamaklı sayı asal sayı olacaktır.
Buna göre I. ve III. haneye gelmesi gereken Braille rakamları aşağıdakilerden hangisidir?
Çakışan kenarlara göre birbirinin yansıması olan rakamlar aşağıdaki gibidir.
Soruda verilen alfabeye göre seçeneklerdeki sayılar aşağıdaki gibidir.
A Seçeneği:
9 ile 5 birbirinin yansıması olduğundan, ilk sayı 95'tir. Yalnız, 95 tam kare olmadığı için doğru cevap A olamaz.
B Seçeneği:
6 ile 4 birbirinin yansımasıdır. Buna göre ilk sayı 64'tür. 64 tam karedir.
5 ile 9 birbirinin yansımasıdır. 59 asal olduğu için doğru cevap B'dir.
C seçeneği:
C seçeneğinde elde edilen iki basamaklı sayılar 64 ve 46'dır. 64 tam kare olduğu halde 46 asal değildir. Doğru cevap C seçeneği olamaz.
D seçeneği:
D seçeneğinde elde edilen iki basamaklı sayılar ise 46 ve 80'dir. 46 tam kare ve 80 asal değildir. Doğru cevap D seçeneği de olamaz.
CEVAP: B

Zeynep parasının yarısı ile paketi 30 lira olan A marka ve diğer yarısı ile paketi 50 lira olan B marka kedi mamalarından alıyor. Bu paketlerden markası aynı olan 6 tanesini evinde beslediği kedileri için ayırdıktan sonra kalan paketleri bir hayvan barınağına veriyor.
Zeynep’in hayvan barınağına verdiği A marka ve B marka mamaların paketlerinin sayıları eşit olduğuna göre Zeynep mamalar için toplam kaç lira harcamıştır?
Zeynep, A ve B marka kedi mamalarına aynı parayı harcadığına göre, ucuz olan A marka mamadan daha fazla almıştır. Markası aynı olan 6 paket mamayı eve bıraktığında kalan paketlerin sayıları eşit olduğundan, eve bıraktığı mamalar A markadır.
B marka kedi mamalarının sayısına x dersek, A marka kedi mamalarının sayısı x + 6 olur. Buna göre, B marka mamalara harcadığı para 50x TL ve A marka mamalara harcadığı para 30(x + 6) TL'dir.
A ve B markalarına aynı parayı verdiği için 50x ile 30(x + 6) ifadeleri eşittir.
50x = 30(x + 6)
⇒ 50x = 30x + 180
⇒ 50x – 30x = 180
⇒ 20x = 180
⇒ x = 9
x = 9 ise, Zeynep'in B marka mamaya verdiği para 50 . 9 = 450 TL'dir. Bu miktar, harcadığı paranın yarısı olduğu için doğru cevap 450 . 2 = 900 TL'dir.
CEVAP: D