BÖLÜM 6: CEBİRSEL İFADELERİ ÇARPANLARA AYIRMA-FARKIN KARESİ

Önceki bölümde, toplamın karesini kullanarak cebirsel ifadeleri çarpanlara ayırmıştık. Bu bölümde, farkın karesini veren özdeşliği kullanarak cebirsel ifadeleri çarpanlara nasıl ayırabileceğimizi öğreniyoruz.

C) a² – 2ab + b² = (a – b)² ÖZDEŞLİĞİNİ KULLANARAK ÇARPANLARA AYIRMA

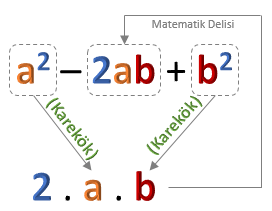
Üç terimli bir cebirsel ifadede terimlerden ikisinin kareköklerinin çarpımının –2 katı üçüncü terime eşitse, bu ifadeyi a² – 2ab + b² = (a – b)² özdeşliğini kullanarak çarpanlara ayırabiliriz. Bu özdeşlikte a ve b yerine terimlerin kareköklerini yazarız.

ÖRNEK:

x² – 6xy + 9y² ifadesini çarpanlara ayıralım.

x²'nin karekökü x'e ve
9y²'nin karekökü 3y'ye eşittir.

x ile 3y'nin çarpımının –2 katı –6xy'ye eşit olduğu için bu ifadeyi a² – 2ab + b² = (a – b)² özdeşliğini kullanarak çarpanlara ayırabiliriz. Bu özdeşlikte a yerine x ve b yerine 3y yazarız.

x² – 6xy + 9y² = (x – 3y)²

Bir özdeşlikte a ve b sayılarını yer değiştirdiğimizde de aynı sonucu elde ederiz. Örneğin, x² – 6xy + 9y² ifadesini hem (x – 3y)² hem de (3y – x)² şeklinde ifade edebiliriz.

ÖRNEK:

... ifadesini çarpanlara ayıralım.

...'nin karekökü ...'e ve
...'ün karekökü ...'ye eşittir.

... ile ...'nin çarpımının ... katı ...'e eşittir.

...

Buna göre verilen ifadeyi a² – 2ab + b² = (a – b)² özdeşliğini kullanarak çarpanlara ayırabiliriz. Bu özdeşlikte a yerine ... ve b yerine ... yazabiliriz.