BÖLÜM 3: DİKDÖRTGENİ KARELERE BÖLME

Bu tarz problemlerde, dikdörtgen şeklinde bir alan, levha veya yüzey eşit karelere bölünür.

Dikdörtgenin en az kaç eşit kareye bölünebileceği veya
Olası en büyük karenin kenar uzunluğu sorulur.

En Büyük Karenin Kenar Uzunluğu

Bir dikdörtgenin, kenar uzunluğu a olan karelere bölünebilmesi için bu dikdörtgenin hem genişliğinin hem de yüksekliğinin a’nın tam katı olması gerekir. Örneğin, aşağıdaki dikdörtgen kenar uzunluğu a birim olan eşit karelere bölünmüştür. Bu dikdörtgenin yüksekliği a birimin 4 katı ve genişliği a birimin 3 katıdır.

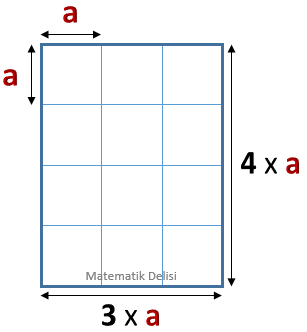
Buna göre, aradığımız karenin bir kenar uzunluğu, dikdörtgenin hem yüksekliğinin hem de genişliğinin böleni olmalıdır.

Dikdörtgeni en az sayıda kareye bölebilmek için, karenin bir kenar uzunluğunun en büyük değerini bulmamız gerekir. Bu değer, dikdörtgenin yüksekliği ile genişliğinin EBOB’una eşittir.

En Az Kare Sayısı

Dikdörtgenin yüksekliğinin ve genişliğinin EBOB'unu alarak, en büyük karenin bir kenar uzunluğunu hesapladıktan sonra, dikdörtgenin en az kaç eşit kareye bölünebileceğini bulabilmek için aşağıdaki yöntemlerden birini kullanabiliriz.

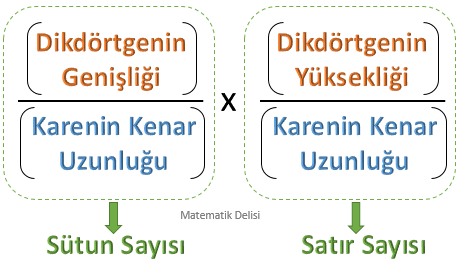
YÖNTEM 1 : Dikdörtgenin genişliğini ve yüksekliğini karenin kenar uzunluğuna bölerek bu dikdörtgenin kaç satır ve kaç sütun kareden oluştuğunu buluruz. Bulduğumuz satır ve sütun sayılarını çarparız.
YÖNTEM 2 : Dikdörtgenin alanını karenin alanına böleriz.

SORU:

Yüksekliği 20 cm ve genişliği 15 cm olan dikdörtgen şeklinde bir kâğıt parçası, eşit karelere bölünmek istenmektedir. Bu kâğıt en az kaç eşit kareye bölünebilir?

ÇÖZÜM:

Eşit karelerin kenar uzunluğu, hem 15'in hem de 20'nin tam böleni olmalıdır. Bu bölenlerden en büyüğü EBOB olduğundan, santimetre cinsinden en büyük karenin kenar uzunluğu 15 ile 20'nin EBOB'una eşittir.

EBOB(15, 20) = 5 olduğu için aradığımız karenin bir kenarı 5 cm uzunluğundadır.

Kağıdın alanı 15 . 20 = 300 cm² ve
Karenin alanı 5 . 5 = 25 cm²'dir.

Buna göre, dikdörtgen şeklindeki kağıt en fazla 300 ÷ 25 = 12 eşit kareye bölünebilir.

EBOB kullanarak bulduğumuz eş kareler, olası en büyük karelerdir. Diğer ortak bölenleri kullanarak, aynı dikdörtgeni daha küçük karelere de bölebiliriz. Bu durumda, daha fazla sayıda eş kare elde ederiz. Yukarıdaki örnekte, karenin kenar uzunluğunu 1 cm seçerek, dikdörtgeni toplam 300 eş kareye bölebiliriz.

SORU:

Bir çiftçi, dikdörtgen şeklindeki tarlasını eşit karelere bölüp, her karenin merkezine 1 adet ceviz ağacı dikecektir. Yaptığı hesaplamalar sonucunda tarlasına bu şekilde en az 18 ceviz ağacı dikebildiğini görmüştür. Buna göre, çiftçinin tarlasının kenar uzunlukları aşağıdakilerden hangisi olabilir?

A) 6 m ve 27 m B) 12 m ve 18 m C) 20 m ve 30 m D) 18 m ve 24 m

ÇÖZÜM:

Seçeneklerdeki sayıların EBOB'larını hesaplayalım.

A) EBOB(6, 27) = 3

B) EBOB(12, 18) = 6

C) EBOB(20, 30) = 10

D) EBOB(18, 24) = 6

Bu sonuçlar, tarlaya sığan en büyük karelerin metre cinsinden kenar uzunluklarıdır. En düşük ağaç sayılarını bulabilmek için verilen dikdörtgenlerin alanlarını karelerin alanlarına bölebiliriz.

A) ...

B) ...

C) ...

D) ...

18 sonucunu veren tek seçenek A olduğu için cevap A'dır.

→KONU ANASAYFASINA DÖN←