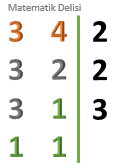
BÖLÜM 2: SAYMA PROBLEMLERİ

EBOB-EKOK problemlerinin çeşitlerinden biri de sayma problemidir.

Sayma problemlerinde,

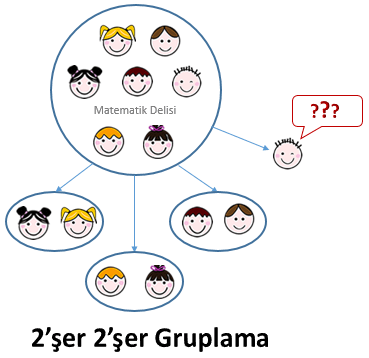
Bir çokluk (öğrenciler, cevizler, paralar, merdiven basamakları vs. ), ikişerli, üçerli vs. gruplara ayrılır.
Gruplama işlemlerinin tümünde, aynı sayıda bütün artar veya eksik kalır.
Çokluğun alabileceği en küçük değer sorulur.

SORU:

Ali, cevizlerini 4’er 4’er, 5’er 5’er ve 6’şar 6’şar saydığında, her defasında 1 ceviz artmaktadır. Buna göre, Ali’nin en az kaç cevizi vardır?

ÇÖZÜM:

Ali cevizleri her saydığında 1 tane artmaktadır. Buna göre, cevizlerin sayısı şu ankinden 1 tane az olsaydı, 4’er 4’er 5’er 5’er ve 6’şar 6’şar saydığında bu cevizlerden artan olmayacaktı. Başka bir deyişle, Ali’deki cevizlerin sayısı 4’e, 5’e ve 6’ya tam bölünecekti.

Ali'nin x tane cevizi olduğunu varsayalım. Yukarıda yaptığımız çıkarıma göre x – 1 sayısı, hem 4’ün hem 5’in hem de 6’nin tam katıdır. 4, 5 ve 6’nın ortak tam katlarından en küçüğü bu sayıların EKOK'una eşit olduğu için x – 1'in alabileceği en küçük değer EKOK(4, 5, 6)'dır.

Kısacası, Ali’nin cevizlerinin 1 eksiği (veya x – 1), EKOK(4, 5, 6) = 60'a eşittir. Buna göre, Ali’nin en az 60 + 1 = 61 cevizi vardır.

Yukarıda bulduğumuz değer Ali'nin ceviz sayısının olası en küçük değeridir. Eğer en küçük sayıyı aramıyorsak, ceviz sayısının 1 eksiği 4, 5 ve 6'nın ortak katı olduğu için x – 1'in değeri 120 de olabilir. Bu nedenle Ali'nin cevizleri 121 tane de olabilir. Benzer şekilde Ali'nin 181, 241, 301, 361,... cevizi de olabilir.

SORU:

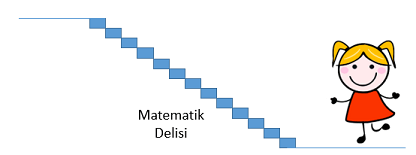
Fatma, bir merdiveni 2’şer 2’şer, 3’er 3’er ve 4’er 4’er çıktığında, her defasında bir basamak artmaktadır. Bu merdiven en az kaç basamaklıdır?

ÇÖZÜM:

Bir önceki sorunun çözümüyle aynı mantığı kullanalım. Merdivendeki basamak sayısı, şu ankinden 1 eksik olsaydı, 2’şer 2’şer, 3’er 3’er ve 4’er 4’er çıkıldığında hiç basamak artmayacaktı. Bu durumda, merdivendeki basamak sayısı 2, 3 ve 4’ün tam katı olacaktı. Bu katlardan en küçüğü 2'nin, 3'ün ve 4'ün EKOK'u olduğu için basamak sayısının 1 eksiği EKOK(2, 3, 4) = 12'dir.

Artan bir basamağı da eklediğimizde, bu merdivendeki basamak sayısının en az 12 + 1 = 13 olduğunu görebiliriz.

SORU:

Bir sınıftaki öğrenciler, sıralara üçer üçer oturduğunda sıralardan birine iki öğrenci; dörder dörder oturduğunda ise sıralardan birine üç öğrenci düşmektedir. Buna göre, bu sınıfta en az kaç öğrenci vardır?

ÇÖZÜM:

Bu sınıfta 1 öğrenci daha olsaydı, öğrenciler sıralara hem 3’er 3'er hem de 4’er 4'er oturduğunda tüm sıralarda eşit sayıda öğrenci olurdu. Böylece öğrenci sayısı hem 3’ün hem de 4’ün tam katı olurdu.