ÇIKMIŞ SORULAR: EŞİTSİZLİKLERLE İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ
Eşitsizliklerle ilgili LGS'de (Liselere Giriş Sınavında) çıkan soruları ve bu soruların çözümlerini aşağıda bulabilirsiniz.
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 1 | 0 | 0 | 1 | 2 | 0 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 1 |
| 2018-2019 | 0 |
| 2019-2020 | 0 |
| 2020-2021 | 1 |
| 2021-2022 | 2 |
| 2022-2023 | 0 |
| 2023-2024 | 1 |
(Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.)
2017-2018 LGS
İki farklı yüzme kursuna ait ücretler aşağıdaki tabloda verilmiştir.
Tablo: Kursların Ücretleri
| Kurslar | Kayıt Ücreti (TL) | Aylık Ücret (TL) |
| 1. Kurs | 310 | 40 |
| 2. Kurs | 130 | 55 |
Yüzme kursuna katılan bir kişi bir defalık kayıt ücreti ve devam ettiği her ay için aylık ücret ödemektedir.
Tabloda ücretleri verilen kurslardan birine katılmak isteyen bir kişinin en az kaç ay kursa devam etmesi durumunda 1. kursa katılması daha ekonomik olur?
Çözüm:
Bu kişinin kurslardan birine toplam x ay devam ettiğini düşünelim.
- 1. kursa katılırsa, 310 TL kayıt ücreti ve 40x kurs ücreti öder. Toplam ücret: 310 + 40x
- 2. kursa katılırsa, 130 TL kayıt ücreti ve 55x kurs ücreti öder. Toplam ücret: 130 + 55x
1. kursun daha ekonomik olabilmesi için aşağıdaki eşitsizliğin sağlaması gerekir.
310 + 40x < 130 + 55x
Eşitsizliğin Çözümü:
Sabit terimleri solda ve x'li terimleri sağda toplayalım.
310 – 130 < 55x – 40x
Sol ve sağ taraftaki işlemleri yapalım.
180 < 15x
İki tarafı da 15'e bölelim.
12 < x
Buna göre, x'in alabileceği en küçük tam sayı değeri 13'tür.
CEVAP: C
2020-2021 LGS
Aşağıdaki yakıt göstergelerinde ibrenin ucu 0'ı gösterdiğinde yakıt deposunun tamamının boş olduğu, 1'i gösterdiğinde tamamının dolu olduğu ve 0 ile 1 arasına eşit aralıklarla konulan çizgilerden herhangi birini gösterdiğinde ise kaçta kaçının dolu olduğu anlaşılmaktadır.
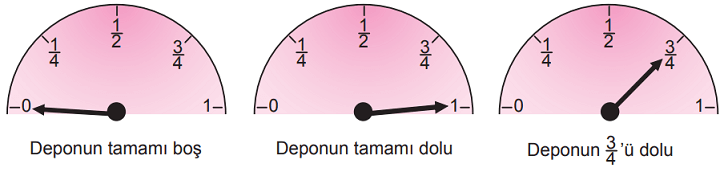
Deposu 48 litre yakıt alabilen bir aracın başlangıçta deposunda 30 litre yakıt bulunmaktadır. Bu araç x litre yakıt tükettikten sonra yakıt göstergesindeki ibrenin ucu ... ile ... arasındaki bir değeri göstermektedir.
Buna göre aracın tükettiği yakıt miktarını litre cinsinden gösteren eşitsizlik aşağıdakilerden hangisidir?
Çözüm:
Deposu 48 litre yakıt alan bir araçta ibrenin ucu ... ile ... arasını gösteriyorsa, bu depodaki yakıt miktarı ... L ile ... L arasındadır. Bu miktar 30 – x'e aittir. Çünkü depodaki 30 litre yakıtın x litresi kullanıldığında geriye 30 – x litre yakıt kalır. Dolayısıyla depoda kalan yakıt miktarı aşağıdaki eşitsizlikle gösterilebilir.
12 < 30 – x < 24
Bu eşitsizlikteki tüm taraflardan 30 çıkarıldığında ortada yalnız –x kalır.
12 – 30 < 30 – x – 30 < 24 – 30
⇒ –18 < –x < –6
Tüm taraflar –1 ile çarpıldığında harcanan yakıt miktarını gösteren eşitsizlik elde edilir.
⇒ (–1) . (–18) > (–1) . (–x) > (–1) . (–6)
⇒ 18 > x > 6
⇒ 6 < x < 18
CEVAP: D
2021-2022 LGS
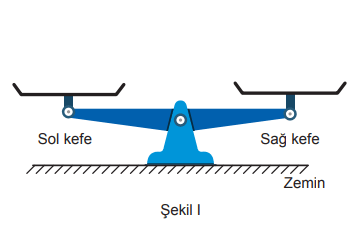
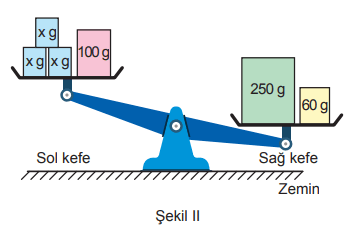
Denge durumundaki eşit kollu terazinin konumu Şekil I'deki gibidir. Bu terazinin sol kefesine bir adet 100 gramlık ve üç adet x gramlık kutu, sağ kefesine ise bir adet 250 gramlık ve bir adet 60 gramlık kutu yerleştirildiğinde denge durumu bozulan terazinin kefelerinin konumu Şekil II'deki gibi olmuştur.
Buna göre, x'in alabileceği değerleri gösteren eşitsizlik aşağıdakilerden hangisidir?
Çözüm:
Terazinin
Sol kefesindeki kutuların toplam kütlesi
x + x + x + 100 = 3x + 100 gramdır.
Sağ kefesindeki kutuların toplam kütlesi ise
250 + 60 = 310 gramdır.
Sağ taraf daha ağır bastığına göre 310 sayısı 3x + 100'den büyüktür.
3x + 100 < 310
Bu eşitsizliğin iki tarafından da 100 çıkaralım.
3x + 100 – 100 < 310 – 100
⇒ 3x < 210
İki tarafı da 3'e bölelim.
x < 70
Bir nesnenin kütlesinin 0'dan büyük olacağını da göz önünde bulundurarak
0 < x < 70
eşitsizliğini yazabiliriz.
CEVAP: D
Bir fabrikanın üç farklı ürün bandında paketlenen ürün sayıları ve bu ürünlerin paketlenme süreleri aşağıdaki tabloda verilmiştir.
Tablo: Paketlenen Ürün Sayıları ve Paketleme Süreleri
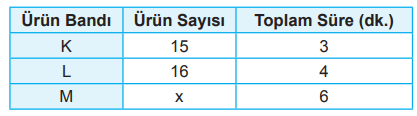
Bu üç bandın her birinde 1 dakikada paketlenen ürün sayısı bir doğal sayıya eşit ve toplamları 13'ten azdır.
Buna göre, x'in alabileceği değer en fazla kaçtır?
Çözüm:
1 dakika içinde
- K bandında paketlenen ürün sayısı 15 ÷ 3 = 5 ve
- L bandında paketlenen ürün sayısı 16 ÷ 4 = 4'tür.
Dolayısıyla, K ve L bantlarında 1 dakikada toplam 5 + 4 = 9 ürün paketlenmektedir. Tüm bantlarda paketlenen toplam ürün sayısı 13'ten az olduğundan M bandından 1 dakikada çıkan ürün sayısı 13 – 9 = 4'ten azdır. 4'ten küçük doğal sayıların en büyüğü 3'tür. 1 dakikada en fazla 3 ürünü paketleyen M bandı, 6 dakikada en fazla 3 × 6 = 18 ürün paketler. Buna göre, x sayısı en fazla 18 olabilir.
CEVAP: C
2023-2024 LGS
Bir mağazada 1 günde satılan pantolon ve gömlek sayısı ve 1'er adetlerinin fiyatları aşağıdaki tabloda verilmiştir.
Tablo: 1 Günde Satılan Pantolon ve Gömlek Sayısı ve 1'er Adetlerinin Fiyatları

Bu mağazada bu ürünlerin satışından toplam 12 000 TL'den az gelir elde edildiğine göre, satılan gömlek sayısı en fazla kaçtır?
Çözüm:
Pantolondan elde edilen gelir
20 · 240 = 4800 TL ve
Gömlekten elde edilen gelir
x · 180 = 180x TL'dir.
Bu iki gelirin toplamı 12 000 TL'den az olmalıdır.
4800 + 180x < 12000
İki taraftan da 4800 çıkaralım.
180x < 12000 – 4800
⇒ 180x < 7200
İki tarafı da 180'e bölelim
x < 7200 ÷ 180
⇒ x < 40
40'tan küçük en büyük tam sayı 39'dur.
CEVAP: B
