ÇIKMIŞ SORULAR: KAREKÖKLÜ İFADELERDE TOPLAMA VE ÇIKARMAYLA İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-1
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 0 | 1 | 0 | 1 | 2 | 2 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 0 |
| 2018-2019 | 1 |
| 2019-2020 | 0 |
| 2020-2021 | 1 |
| 2021-2022 | 2 |
| 2022-2023 | 2 |
| 2023-2024 | 1 |
Aşağıda, LGS sınavlarında kareköklü sayıların toplanmasıyla ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2018-2019 LGS
..., ... ve ... birer gerçek sayı ve ... ≥ 0 olmak üzere
...
... ...
... ...
Aşağıdaki şekildeki gibi bir vincin havada tuttuğu inşaat malzemesinin yerden yüksekliği ... m ve malzemenin vincin koluna uzaklığı ... mʼdir.
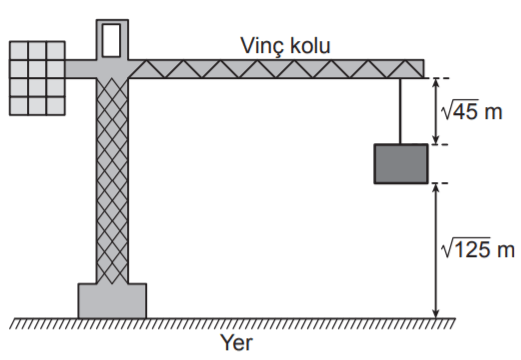
Vincin kolunun yerden yüksekliği sabit kalmak üzere malzeme şekildeki konumdayken ... m yukarı çekiliyor.
Buna göre son durumda malzemenin yerden yüksekliği, malzemenin vincin koluna uzaklığından kaç metre fazladır?
Çözüm:
Soruda verilen uzaklıkları kök dışına çıkaralım.
- Malzemenin yerden yüksekliği: ... ... m
- Malzemenin vinç koluna uzaklığı: ... ... m
Malzeme ... m yukarı çekilirse, yeni uzaklıklar aşağıdaki gibi olur.
- Malzemenin yerden yükseliği: ... ... m
- Malzemenin vinç koluna uzaklığı: ... ... m
Buna göre, uzaklıklar arasındaki yeni fark ... ... m olur.
CEVAP: C
2020-2021 LGS
..., ..., ... birer doğal sayı olmak üzere
...
... ... dir.
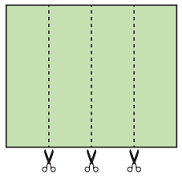
Dikdörtgen şeklindeki bir kâğıt, yukarıdaki gibi kesilerek dikdörtgen şeklinde dört eş parça elde edilmiştir. Bu parçaların kısa kenarları ile uzun kenarları çakıştırılarak aşağıdaki gibi iki farklı şekil oluşturulmuştur.
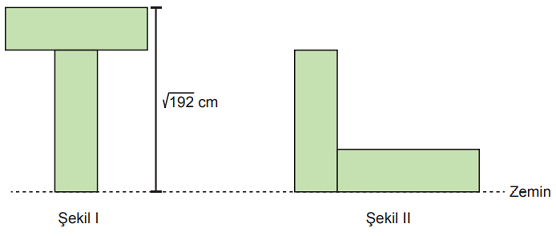
Şekil I'in yüksekliği ... cm ve Şekil II'nin çevresinin uzunluğu ... cm'dir.
Buna göre başlangıçta verilen dikdörtgen şeklindeki kâğıdın bir yüzünün alanı kaç santimetrekaredir?
Çözüm:
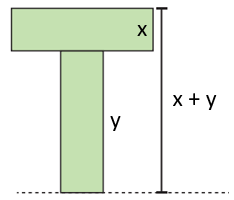
Parçaların kısa kenarına x ve uzun kenarına y dersek Şekil I'in yüksekliğini x + y şeklinde ifade edebiliriz. Bu uzunluk ... ... cm'ye eşittir.
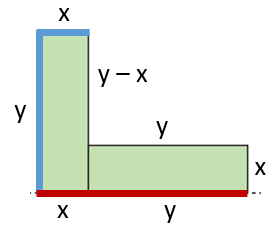
Şekil II üzerinde hem mavi hem de kırmızı ile işaretlediğimiz hatlardan her birinin uzunluğu x + y'ye ve dolayısıyla ... cm'ye eşittir.
Şekil II'nin çevre uzunluğundan bu iki hattın uzunluklarını çıkardığımızda geriye ... cm kalır.
... ...
Bu uzunluk y – x + y + x = 2y'ye eşittir. Buna göre ... cm ve ... ... cm'dir.
Dikdörtgen şeklindeki parçalardan birinin alanı kenar uzunluklarının çarpımına eşittir.
... ... cm2
Dolayısıyla, başlangıçtaki kağıdın bir yüzünün alanı 4 . 36 = 144 cm2'dir.
CEVAP: B
2021-2022 LGS
a, b, c, d birer doğal sayı olmak üzere
...
... ...
... ...
... ... dir.

Çevresinin uzunluğu ... cm olan dikdörtgen şeklindeki kâğıt, yukarıdaki gibi dikdörtgen ve kare şeklinde iki parçaya ayrılıyor.
Kare şeklindeki parçanın bir kenar uzunluğu ... cm olduğuna göre dikdörtgen şeklindeki parçanın bir yüzünün alanı kaç santimetrekaredir?
Çözüm:
- ... ... ve
- ... ...'dir.
Buna göre, başlangıçtaki şeklin çevresi ... cm ve karenin kenar uzunluğu ... cm'dir.
Bildiğimiz uzunlukları şekil üzerinde gösterelim.
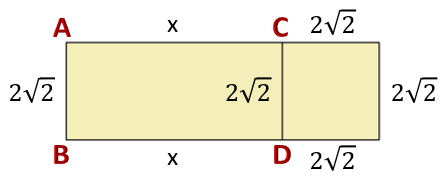
Dikdörtgenin kısa kenarı, karenin kenar uzunluğu ile aynıdır. (|AB| = |CD| = ...)
Dikdörtgen şeklindeki parçanın uzun kenarına ... diyelim. Parçalara ayrılmadan önceki kâğıdın santimetre cinsinden çevresi 4 tane ... ile 2 tane ...'in toplamına eşit olur. Bu ifade ... ... şeklinde gösterilebilir.
Çevre için bulduğumuz ifadeyi ...'ye eşitleyerek ...'in değerini elde edebiliriz.
...
⇒ ...
⇒ ...
⇒ ...
Kenar uzunlukları ... cm ve ... cm olan bir dikdörtgenin bir yüzünün alanı
... ... ... cm2'dir.
CEVAP: B
..., ..., ... birer doğal sayı olmak üzere
...
... ...
... ...
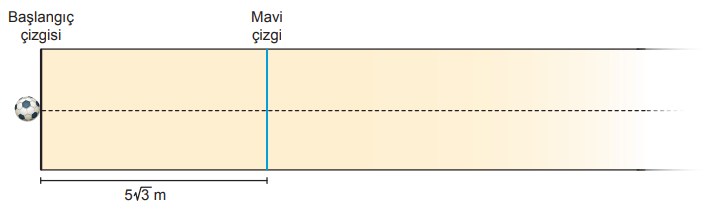
Aşağıdaki oyun parkurunda birbirine paralel olan başlangıç çizgisi ve mavi çizgi arasındaki uzaklık ... m'dir. Başlangıç çizgisinden Fatih, Yavuz ve Mehmet doğrusal bir çizgi boyunca top yuvarlayacaklardır. Topu, mavi çizgiye en yakın mesafede duran kişi oyunu kazanacaktır.
Oyunun sonunda Fatih'in yuvarladığı topun durduğu mavi çizgiye uzaklığı ... m, Yavuz'un yuvarladığı topun durduğu noktanın başlangıç çizgisine uzaklığı ise ... m'dir. Bu durumda Fatih birinci, Mehmet ikinci ve Yavuz üçüncü olmuştur.
Buna göre, Mehmet'in yuvarladığı topun durduğu noktanın başlangıç çizgisine uzaklığının metre cinsinden değeri aşağıdakilerden hangisi olabilir?
Çözüm:
- Fatih'in topunun mavi çizgiye uzaklığı ... m ve
- Yavuz'un topunun mavi çizgiye uzaklığı ... ... m'dir.
Buna göre Mehmet'in topunun mavi çizgiye uzaklığı ... m ile ... m arasında olmalıdır. Yalnız, soruda Mehmet'in yuvarladığı topun mavi çizginin solunda mı yoksa sağında mı durduğu verilmemiştir. Her iki durumu da ayrı ayrı inceleyelim.
Mavi çizginin solu:
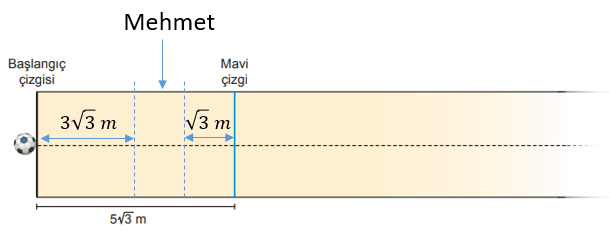
Bu durumda Mehmet'in topunun başlangıç noktasına uzaklığı ... m ile ... m arasında olmalıdır.
- ... ...
- ... ...
27 ile 48 arasındaki tek tam kare sayı 36'dır. Yalnız ... sayısı seçeneklerde olmadığı için Mehmet'in topunun mavi çizginin sağında durduğu durumu değerlendirmemiz gerekir.
Mavi çizginin sağı
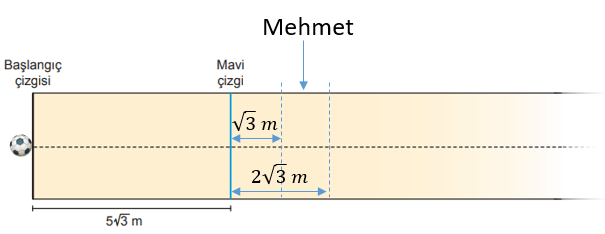
Mehmet'in topu mavi çizginin sağında durduysa, başlangıç noktasına uzaklığı ... ... m ile ... ... m arasındadır.
- ... ...
- ... ...
108 ile 147 arasındaki tam kare sayılar 121 ve 144'tür. Buna göre, Mehmet'in topunun başlangıç noktasına uzaklığı ... m veya ... m olabilir.
CEVAP: D
2022-2023 LGS
..., ..., ... birer doğal sayı olmak üzere
...
... ...
... ... dir.
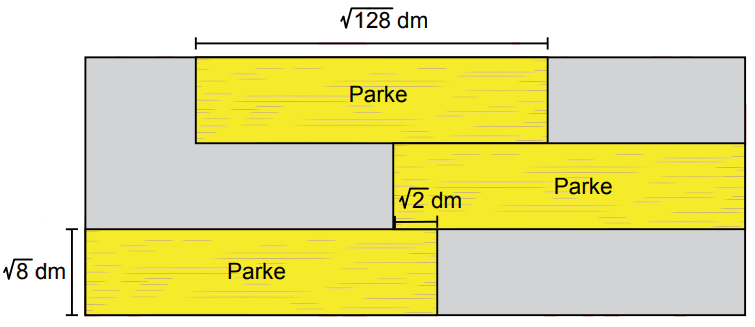
Yukarıda verilen dikdörtgen şeklindeki bir zemine parke döşenmektedir. Zeminde döşeli dikdörtgen biçiminde üç özdeş parke ile ilgili bazı ölçüler şekilde verilmiştir.
Buna göre, parke döşenmemiş bölgelerin alanları toplamı kaç desimetrekaredir?
Çözüm:
Görseldeki parkenin taban ve yüksekliğini aşağıdaki gibi yazabiliriz.
Taban: ... ... dm
Yükseklik: ... ... dm
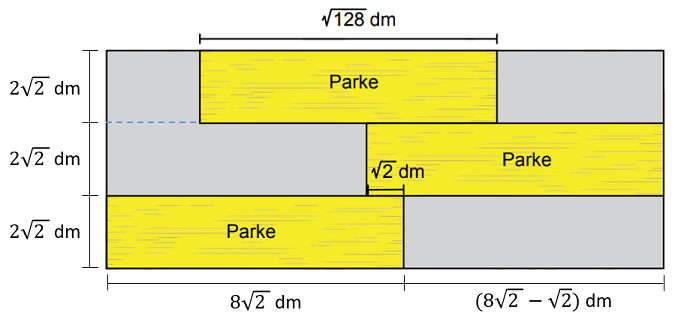
Zemini ifade eden dikdörtgenin yüksekliği 3 parkenin yüksekliklerinin toplamına eşittir.
... ... dm
Tabanı ise iki parkenin taban uzunlukları toplamından ... dm azdır.
... ... dm
Buna göre zeminin toplam alanı
... ... ... dm2'dir.
Her bir parkenin alanı
... ... ... dm2
olduğundan 3 parkenin toplam alanı 3 × 32 = 96 dm2'dir. Dolayısıyla, zeminde parke döşenmemiş alanların toplamı
180 – 96 = 84 dm2'dir.
CEVAP: B
