SÜRE
15:00DOĞRUSAL DENKLEMLER VE GRAFİKLERİ
ÇÖZÜMLÜ KONU TESTİ

SÜRE
15:00
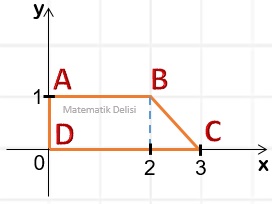
ABCD yamuğunun [BC] kenarı aşağıdaki doğrulardan hangisinin üzerindedir?
ABCD yamuğunun [BC] kenarını her iki yönde devam ettirdiğimizde (0, 3) ve (3, 0) noktalarından geçen bir doğru elde ederiz.
Doğrunun genel denklemi ax + by + c = 0'dır. (3, 0) noktasından geçen bir denklemde x yerine 3 ve y yerine 0 koyduğumuzda eşitliğin sağlanması gerekir.
a . 3 + b . 0 + c = 0
⇒ 3a + c = 0
Benzer şekilde (0, 3) noktasının apsis ve ordinatını denklemde yerine yazarsak
3b + c = 0
eşitliğini elde ederiz. Bu eşitlikte b yerine 1 yazarsak c = –3 olur. c'nin bu değerini 3a + c = 0 denkleminde yerine koyarsak a = 1 olur. Buna göre aradığımız denklem x + y – 3 = 0 veya x + y = 3'tür.
Bu sonuca, seçeneklerdeki hangi denklemin (3, 0) ve (0, 3) noktalarından geçtiğini test ederek de ulaşabiliriz.
CEVAP: A
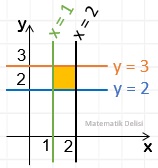
x = 5 ve y = 3 doğrularının kesişim noktası ile orijinden geçen doğrunun denklemi aşağıdakilerden hangisidir?
Orijinden geçen doğruların genel denklemi ax + by = 0 veya başka bir ifadeyle ax = –by'dir. Bu forma sahip olan denklemler A ve B seçeneklerinde verilmiştir.
x = 5 ve y = 3 doğrularının kesişim noktası (5, 3) noktasından geçiyorsa, x yerine 5 ve y yerine 3 yazdığımızda denklemdeki eşitliğin sağlanması gerekir. A seçeneğinde verilen denklemde bu işlemi yaptığımızda geçerli bir eşitlik elde ederiz.
3 . 5 = 5. 3
CEVAP: A
A sıfırdan farklı bir gerçek sayı ise, Ax + Ay + A = 0 doğrusunun grafiği aşağıdakilerden hangisidir?
Bir denklemdeki tüm terimlerin 0'dan farklı bir sayıya bölünmesi bu denklemin grafiğini değiştirmez. Ax + Ay + A = 0 denklemindeki tüm terimleri A'ya böldüğümüzde x + y + 1 = 0 denklemini elde ederiz. Bu denklemde x yerine 0 yazdığımızda y = –1 ve y yerine 0 yazdığımızda x = –1 sonuçlarını elde ettiğimiz için aradığımız doğru, (0, –1) ve (–1, 0) noktalarından geçer.
Doğru grafik D seçeneğinde verilmiştir.
CEVAP: D
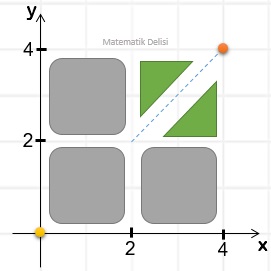
Yukarıda bir sitenin kuşbakışı görüntüsü verilmiştir. Bu grafikte, boyalı alanlar binaları ve diğer alanlar bu sitedeki otoyolları göstermektedir.
A noktasından arabayla yola çıkan biri hangi seçenekteki doğruları sırayla takip ederek B noktasına ulaşamaz?
A, B ve C seçeneklerindeki rotalar aşağıda gösterilmiştir.
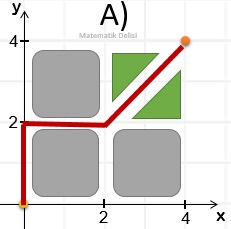
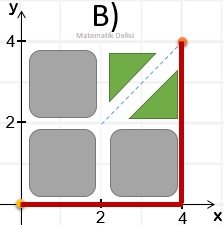
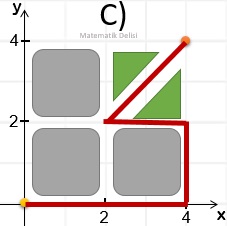
D seçeneğinde verilen doğrular üzerinden geçerek B noktasına ulaşılamaz.
CEVAP: D
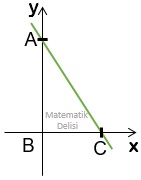
ABC üçgenine ait [AC] doğru parçası, 3x + 3y = 12 doğrusunun üzerindeyse, ABC üçgeninin alanı kaç birimkaredir?
3x + 3y = 12 denkleminde x yerine 0 yazdığımızda
3y = 12
⇒ y = 4
sonucuna ulaşırız. Buna göre, A noktası y ekseninde 4 noktasına denk gelir ve |BC| yüksekliği 4 birimdir.
Benzer şekilde 3x + 3y = 12 denkleminde y yerine 0 koyduğumuzda
3x = 12
⇒ x = 4
sonucuna ulaşırız. Bu sonucu kullanarak ABC üçgeninin tabanının 4 birim olduğunu görebiliriz.
Taban uzunluğu ve yüksekliği 4 birim olan bir üçgenin alanı ... birimkaredir.
CEVAP: A
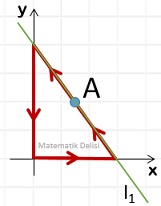
Yukarıdaki şekilde l1 doğrusunun denklemi 4x + 3y = 12'dir.
l1 doğrusu üzerindeki A noktasından başlayarak kırmızı renkle gösterilen yol üzerinde ok yönünde ilerleyerek tekrar aynı noktaya ulaşana kadar yürüyen Esra, toplam kaç birim yol katetmiştir?
Esra'nın izlediği yol bir dik üçgendir. Bu üçgenin kenar uzunluklarını bulabilmek için 4x + 3y = 12 denklemine ait doğrunun eksenleri kestiği noktaları hesaplamamız gerekir.
Denklemde y yerine 0 yazarak bu doğrunun x eksenini x = 3 noktasında kestiğini görebiliriz.
4x + 0 = 12
⇒ x = 3
Benzer şekilde, x yerine 0 yazarak aynı doğrunun y eksenini y = 4 noktasında kestiğini görebiliriz.
0 + 3y = 12
⇒ y = 4
Buna göre, dik üçgenin yüksekliği 4 birim ve tabanı 3 birimdir. Hipotenüsü bulabilmek için Pisagor Teoremini kullanırsak, bu uzunluğun
... birim
olduğunu görebiliriz.
Esra'nın üzerinde yürüdüğü üçgenin kenar uzunlukları 3, 4 ve 5 birim olduğuna göre, yürüdüğü toplam yol 3 + 4 + 5 = 12 birimdir.
CEVAP: B
Aşağıdaki seçeneklerin hangisinde verilen doğrular arasında kalan şekil bir dikdörtgendir?
C seçeneğinde verilen doğruların arasında kalan şekil bir dikdörtgendir.
Diğer seçeneklerdeki doğrular arasında dikdörtgen şeklinde bir alan kalmaz.
CEVAP: C

3 birim yarıçapında bir duvar saati koordinat sistemine yukarıdaki gibi yerleştirilmiştir.
Barış bir filmi izlemeye başladığında bu saatin akrebi y = 3 ve yelkovanı x = 3 doğrusu üzerindedir.
Film bittiğinde ise hem akrep hem de yelkovan x = 3 doğrusunun üzerinde ise Barış'ın izlediği film ne kadar sürmüş olabilir?
Saat 3:00, 9:00, 15:00 veya 21:00 olduğunda akrep y = 3 ve yelkovan x = 3 üzerindedir.
Hem akrebin hem de yelkovanın x = 3 üzerinde olduğu durum ise saat 6:00, 12:00, 18:00 ve 00:00'da gerçekleşir.
Buna göre filmin başlangıç ve bitiş süreleri arasındaki fark 3 saat olabilir. Örneğin, Barış bu filmi izlemeye saat 9:00'da başlayıp, saat 12:00'da izlemeyi bitirmiş olabilir.
Elde ettiğimiz başlangıç ve bitiş zamanları arasında diğer seçeneklerdeki kadar farklar elde edilemez.
CEVAP: B
x + By = 5 denkleminin (1, 2) noktasından geçebilmesi için B'nin alabileceği değerler toplamı kaçtır?
x + By = 5 doğrusunun (1, 2) noktasından geçebilmesi için x yerine 1 ve y yerine 2 yazdığımızda bu denklemdeki eşitliğin sağlanması gerekir. Buna göre
1 + B . 2 = 5
⇒ 2B = 4
⇒ B = 2
olur. B'nin alabileceği tek değer 2 olduğu için alabileceği değerler toplamı da 2'dir.
CEVAP: A
Ax + y = 0 ile y = 4 doğrularının kesişim noktasının apsisi 2 ise A'nın değeri aşağıdakilerden hangisine eşittir?
Ax + y = 0 ve y = 4 doğrularının kesişim noktası, her iki doğrunun da üzerindedir. y = 4 doğrusunun üzerindeki tüm noktaların ordinatı 4 olduğu için kesişim noktasının ordinatı da 4'tür. Bu noktanın apsisi 2 ise, koordinat sisteminde (2, 4) şeklinde gösterilebilir. (2, 4) noktası aynı zamanda Ax + y = 0 doğrusunun üzerinde olduğu için x yerine 2 ve y yerine 4 yazdığımızda eşitliğin sağlanması gerekir. Buna göre
A . 2 + 4 = 0
⇒ 2A = –4
⇒ A = –2'dir.
CEVAP: A