TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ AÇIORTAYLARIN KESİŞİMİ
TEOREMLER VE İSPATLAR
ÜÇGENDE AÇIORTAYLAR NEDEN BİR NOKTADA KESİŞİRLER?
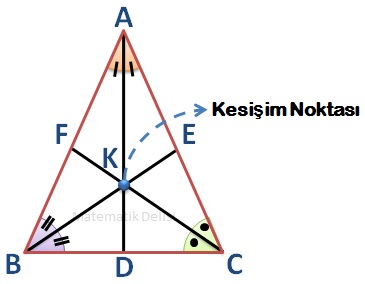
📚 Bir üçgendeki tüm açıortaylar bir noktada kesişirler.
İSPAT
Bir dik üçgendeki tüm açıortayların bir noktada kesiştiğini ispatlayabilmek için açıortaylardan ikisini çizip, üçüncü açıortayın çizdiğimiz açıortayların kesişim noktasından geçtiğini gösteriyoruz.
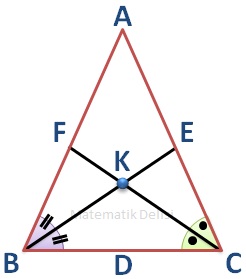
Bir ... üçgeninde ... ve ... açılarının açıortaylarını çizip, kesişim noktasına K diyelim.

K noktasından AB, AC ve BC kenarlarına dik indirelim.
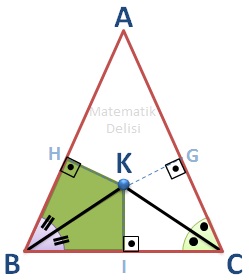
Tüm iç açıları aynı olduğu için ... ve ... üçgenleri benzerdir. Bu iki üçgenin hipotenüsleri de aynı olduğu için ... ve ... üçgenleri aynı zamanda eş üçgenlerdir. Bu da |HK| ve |KI| uzunluklarının eşit olduğunu gösterir.
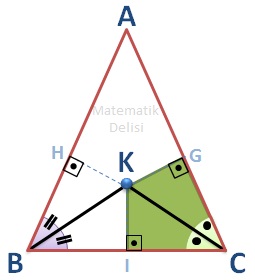
Benzer şekilde ... ve ... üçgenleri de eş üçgenlerdir ve dolayısıyla |KI| ve |KG| uzunlukları da eşittir.
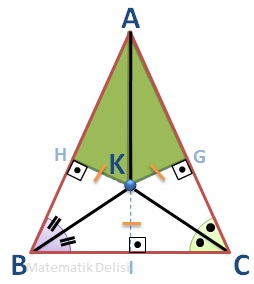
A ve K noktalarının arasına bir doğru parçası çizerek, ... ve ... dik üçgenlerini oluşturalım. Bu dik üçgenlerin hipotenüsleri ortaktır ve |HK| = |GK|'dır. Buna göre, üçüncü kenar uzunlukları da eşit olmalıdır (|AH| = |AG|). Tüm kenarları eşit olduğundan, ... ve ... üçgenlerinin eş olduklarını ve dolayısıyla ... ve ... açılarının eşit olduğunu söyleyebiliriz. Bu nedenle, AK doğru parçasının üçüncü açıortayın bir parçası olduğu sonucuna erişebiliriz. Buna göre, ... açısının açıortayı ... ve ... açılarının açıortaylarının kesişim noktasından geçer. Başka bir değişle, bir üçgendeki tüm açıortaylar bir noktada kesişirler.
TEOREMLER VE İSPATLAR ➤ ÜÇGENLER ➤ AÇIORTAYLARIN KESİŞİMİ