BÖLÜM 1: ÜÇGENLERDE BENZERLİK
Benzer üçgenlerin iki temel özelliği vardır.
- İç açıları eşittir.
- Kenar uzunlukları arasında sabit bir oran vardır.
Bu özelliklerden birini sağlayan üçgenler diğerini de sağlar. Dolayısıyla, üçgenlerin benzer olup olmadığını anlamak için bu özelliklerden birini test etmek yeterlidir.
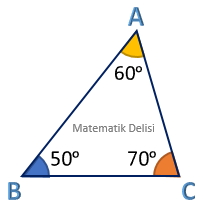
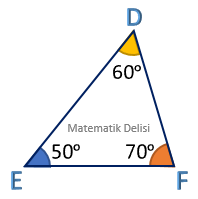
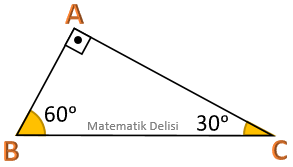
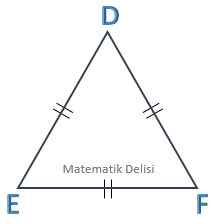
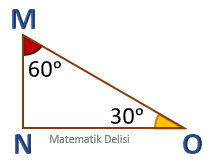
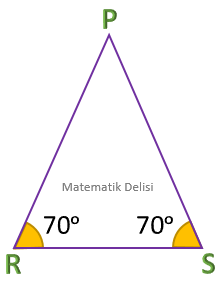
ABC ve DEF üçgenlerinin iç açıları aynı olduğundan bu üçgenler benzerdir.
..., ... ve ...'dir.
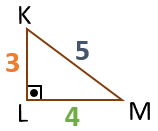
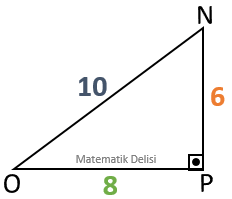
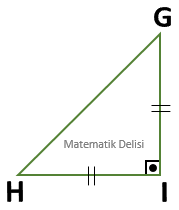
NPO üçgeninin kenar uzunlukları, KLM üçgeninin kenar uzunluklarının
|NP| =
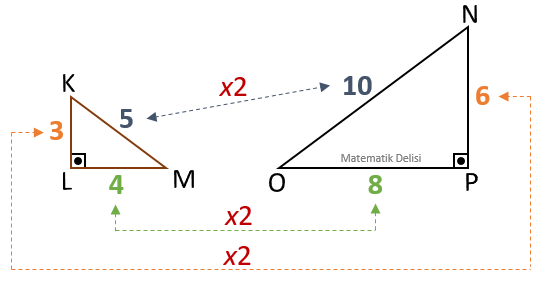
Kenar uzunlukları arasında sabit bir oran bulunduğu için KLM ve NPO üçgenleri benzerdir.
Üçgenler arasındaki benzerlik ~ sembolü ile gösterilir. Örneğin, ABC ve DEF üçgenlerinin
benzer olduğu ABC ~ DEF şeklinde gösterilir. Bu gösterimde üçgenleri simgeleyen harflerin sıralaması önemlidir. Aynı açıya sahip olan köşeler, aynı
sırayla yazılır. Örneğin, ABC ~ DEF ise
...,
... ve
...'dir.
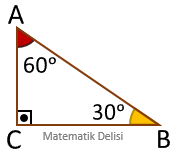
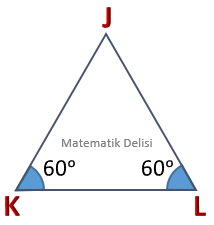
Yukarıdaki üçgenlerde ..., ... ve ...'dir. Bu üçgenler arasındaki benzerlik ABC ~ KLM, BAC ~ LKM, CAB ~ MKL vs. şeklinde gösterilebilir.
Benzer üçgenlerden birine uygulanan
öteleme,
yansıma ve
dönme hareketleri sonucunda benzerlik bozulmaz.
Benzer üçgenler, hem
iç açılarına hem de
kenar uzunluklarına göre
aynı çeşit üçgenlerdir. Örneğin, ikizkenar bir üçgene benzer üçgenlerin tümü ikizkenardır. Geniş açılı bir üçgene benzer üçgenlerin tümü geniş açılıdır.
